Файл: Е. М. Лукина должность, уч степень, звание подпись, дата инициалы, фамилия контрольная работа по дисциплине Статистика.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 29.11.2023

Просмотров: 74

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Вариант 5

Решение

Решение

Решение

Решение

Решение

Решение

Решение




̅

Среднюю хронологическую ряда динамики рассчитаем по формуле:








Средний абсолютный прирост равен:
̅ ̅̅ ̅
Средний темп роста:






̅̅̅



 √

· √




Средний темп прироста:

̅̅̅ ̅ ̅ ̅ ̅ ̅

Таким образом, ожидаемая продолжительность жизни при рождении в период 2009-2018 гг. увеличилась с 68,78 до 72,91 лет (на 4,31 года). Средняя ожидаемая продолжительность жизни за анализируемый период составила 70,84 лет. С каждым годом в среднем ожидаемая продолжительность жизни увеличивалась на 0,41 лет, или 0,65%.

Задача 6. Имеются данные о выпуске и фонде заработной платы:


Выпуск

продукции, тыс. шт.

84

95

97

110

121

161

166

171

175

174

186

210

251

Фонд заработной платы, млн.

руб.

2,0

2,3

1,5

2,8

4,2

2,6

2,2

3,5

8,5

4,2

4,6

3,9

6,5

Найти уравнение корреляционной связи (уравнение регрессии) между выпуском продукции и фондом заработной платы (связь в виде параболы). Исходные данные и теоретическую зависимость представить на графике. Определить среднюю ошибку аппроксимации.

Рассчитать индексы детерминации и корреляции. Сделать выводы.

Решение


Для уравнения параболы второго порядка параметры могут быть определены на основе решения следующей системы нормальных уравнений методом наименьших квадратов:

∑ ∑ ∑

∑ ∑ ∑ ∑

{ ∑ ∑ ∑ ∑

Составим вспомогательную таблицу:


x




xy




y

84
2
7056
168
592704
49787136
14112

95
2,3
9025
218,5
857375
81450625
20758

97
1,5
9409
145,5
912673
88529281
14114

110
2,8
12100
308
1331000
146410000
33880

121
4,2
14641
508,2
1771561
214358881
61492

161
2,6
25921
418,6
4173281
671898241
67395

166
2,2
27556
365,2
4574296
759333136
60623

171
3,5
29241
598,5
5000211
855036081
102344

175
8,5
30625
1487,5
5359375
937890625
260313

174
4,2
30276
730,8
5268024
916636176
127159

186
4,6
34596
855,6
6434856
1196883216
159142

210
3,9
44100
819
9261000
1944810000
171990

251
6,5
63001
1631,5
15813251
3969126001
409507

2001
48,8
337547
8254,9
61349607
11832149399
1502826


{

По рассчитанным параметрам уравнение параболы второго порядка примет вид:

̅

Для проверки адекватности рассчитаем среднюю ошибку аппроксимации по формуле:



∑ |

(

|



x


(

(

(

| |

84
2
1,97
0,03
0,0155

95
2,3
2,26
0,04
0,0185

97
1,5
2,31
-0,81
0,5398

110
2,8
2,65
0,15
0,0543

121
4,2
2,93
1,27
0,3019

161
2,6
3,95
-1,35
0,5191

166
2,2
4,08
-1,88
0,8523

171
3,5
4,20
-0,70
0,2000

175
8,5
4,30
4,20
0,4941

174
4,2
4,27
-0,07
0,0178

186
4,6
4,57
0,03
0,0059

210
3,9
5,16
-1,26
0,3237

251
6,5
6,15
0,35
0,0540

2001
48,8
48,8
-
3,3970





Поскольку ошибка больше 7%, то данное уравнение не рекомендуется использовать в качестве тренда.

Исходные данные и теоретическую зависимость представим на графике:


у, млн. руб.


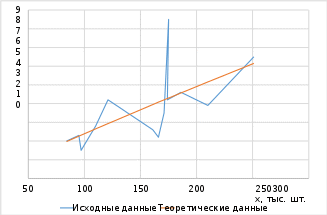Рис. 1 – График зависимости

Рассчитаем коэффициенты детерминации и корреляции для выявления тесноты связи между выпуском продукции и расходами материала на единицу продукции.


∑(

∑( ̅




̅
( ̅

(

(

( (

2
-1,754
3,076
1,97
0,03
0,0009

2,3
-1,454
2,114
2,26
0,04
0,0016

1,5
-2,254
5,080
2,31
-0,81
0,6561

2,8
-0,954
0,910
2,65
0,15
0,0225

4,2
0,446
0,199
2,93
1,27
1,6129

2,6
-1,154
1,331
3,95
-1,35
1,8225

2,2
-1,554
2,414
4,08
-1,88
3,5344

3,5
-0,254
0,064
4,2
-0,7
0,49

8,5
4,746
22,526
4,3
4,2
17,64

4,2
0,446
0,199
4,27
-0,07
0,0049

4,6
0,846
0,716
4,57
0,03
0,0009

3,9
0,146
0,021
5,16
-1,26
1,5876

6,5
2,746
7,541
6,15
0,35
0,1225

48,8
-
46,19
48,8
-
27,5

Смотрите также файлы