Файл: Задача 1 Вычислить двойной интеграл от функции по заданной области . Решение Вид области представлен на рисунке.doc
Добавлен: 29.11.2023
Просмотров: 70
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Вариант №6
Задача №1
Вычислить двойной интеграл
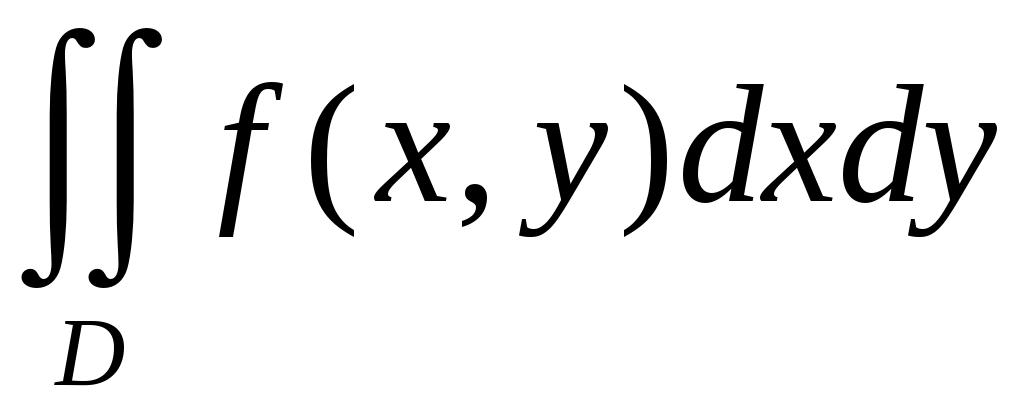от функции 
по заданной области 
:
, 
.Решение
Вид области
представлен на рисунке
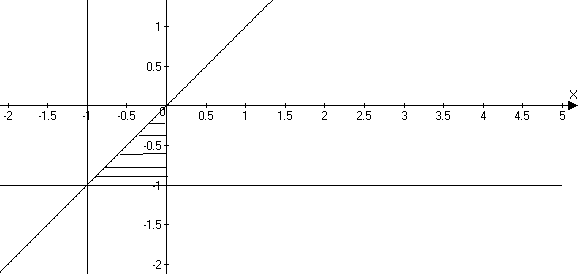
Представим двойной интеграл через повторный:
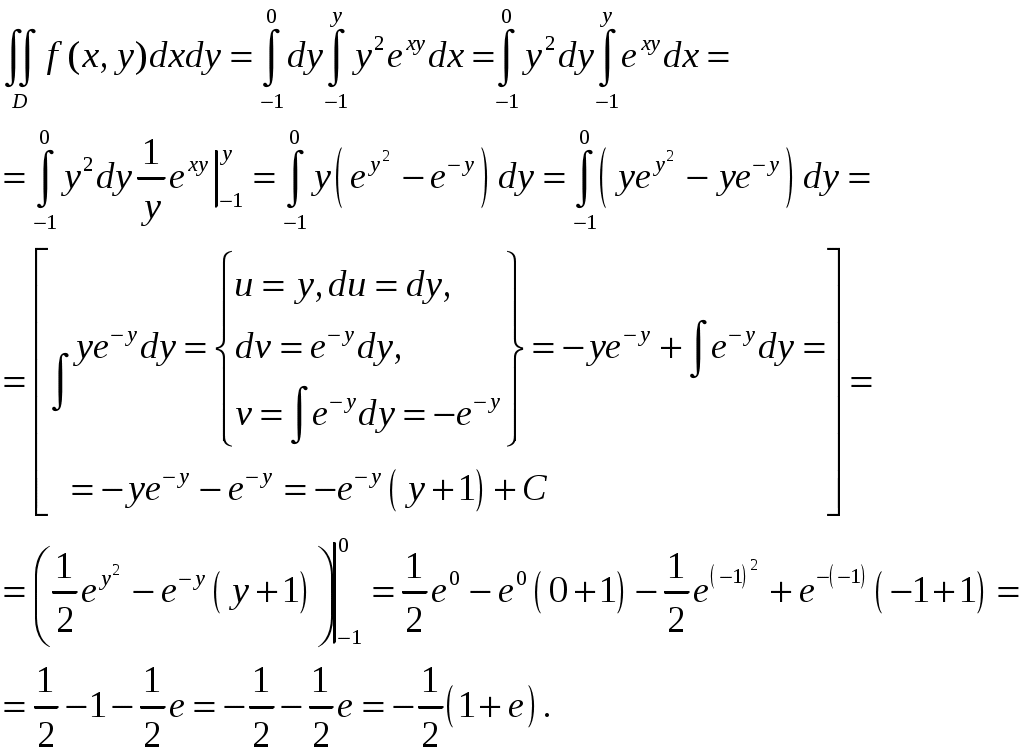
Задача №2
Вычислить объём тела
с помощью кратного интеграла, используя подходящую замену переменных:
.
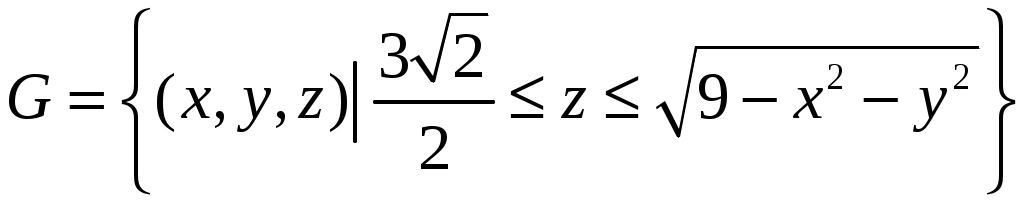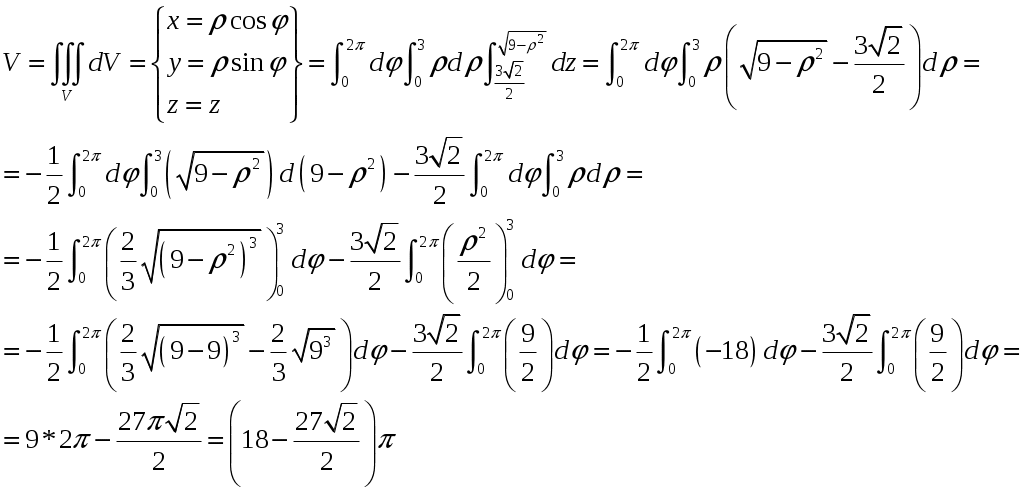
Задача №3
Вычислить криволинейный интеграл I рода по плоской кривой
:
, – четверть окружности 
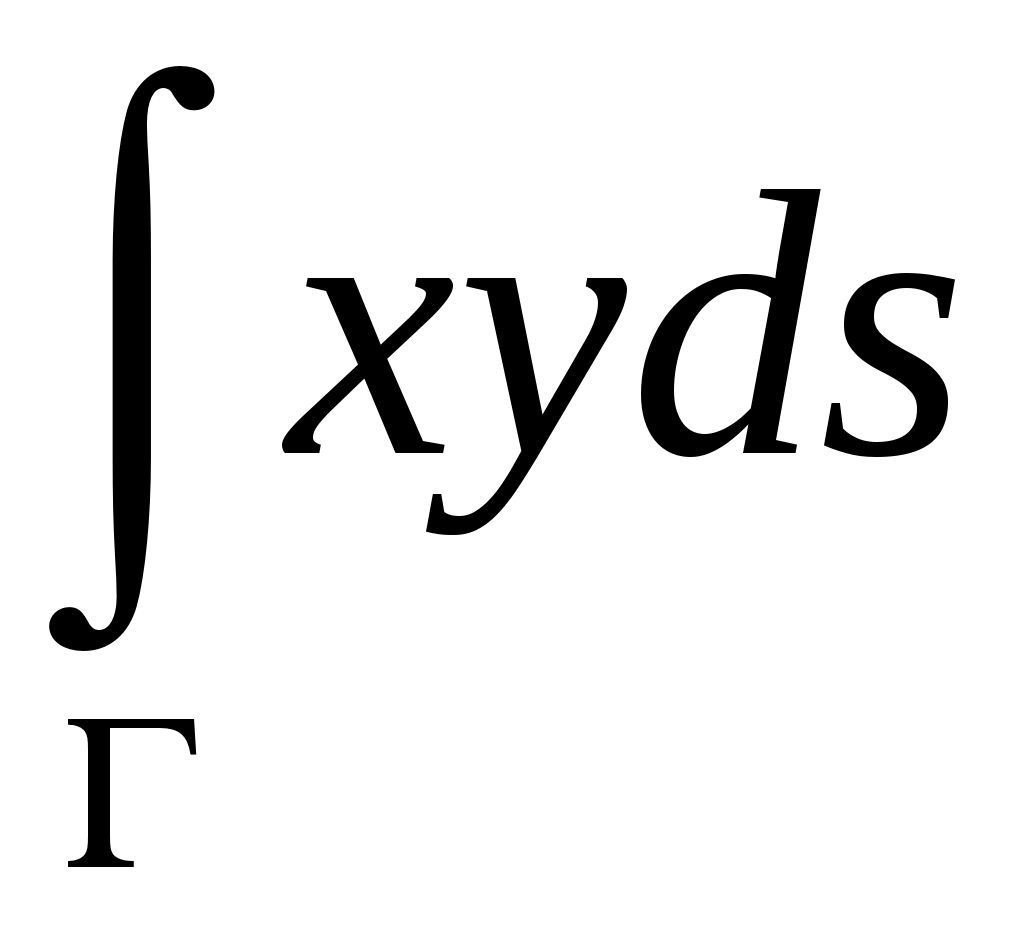, лежащая в первом квадранте.Решение. Рассматривая х как параметр, получаем:
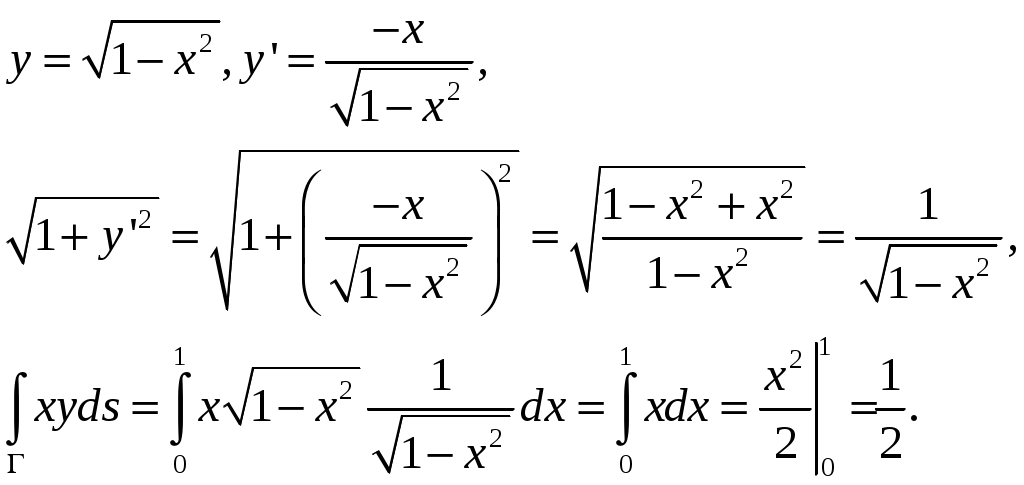
Задача №4
Вычислить криволинейный интеграл по меньшей дуге единичной окружности, заключённой между точками
и 
и ориентированной в направлении от точки к точке
:
, 
, 
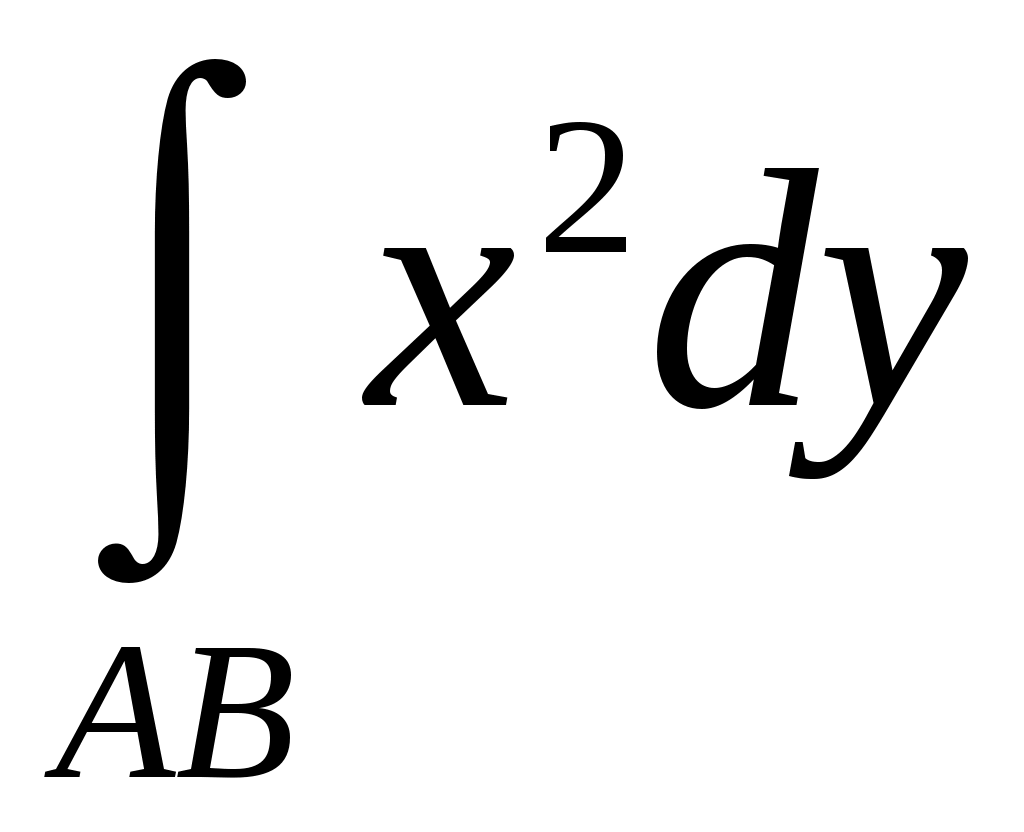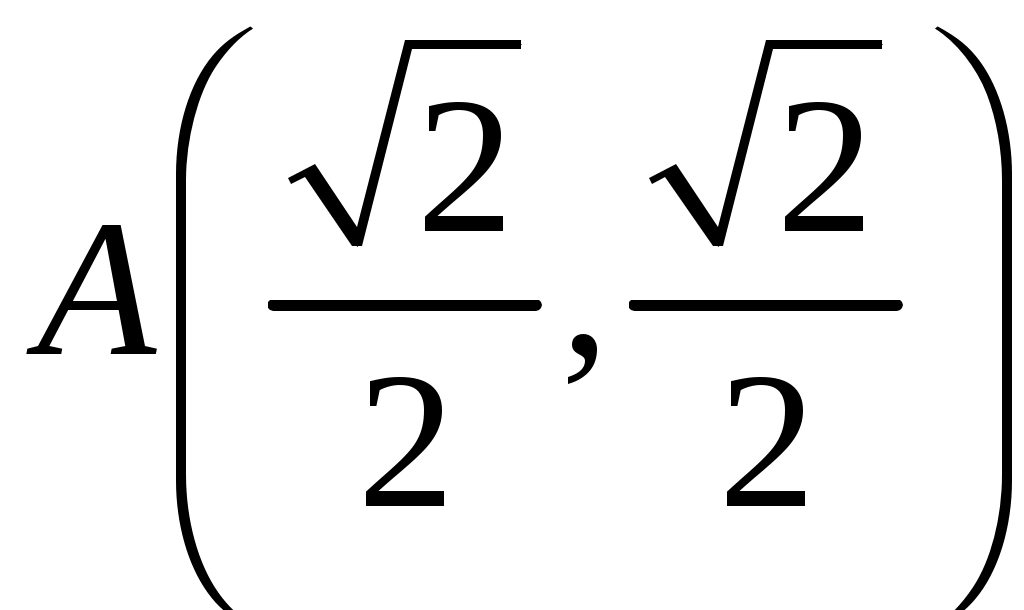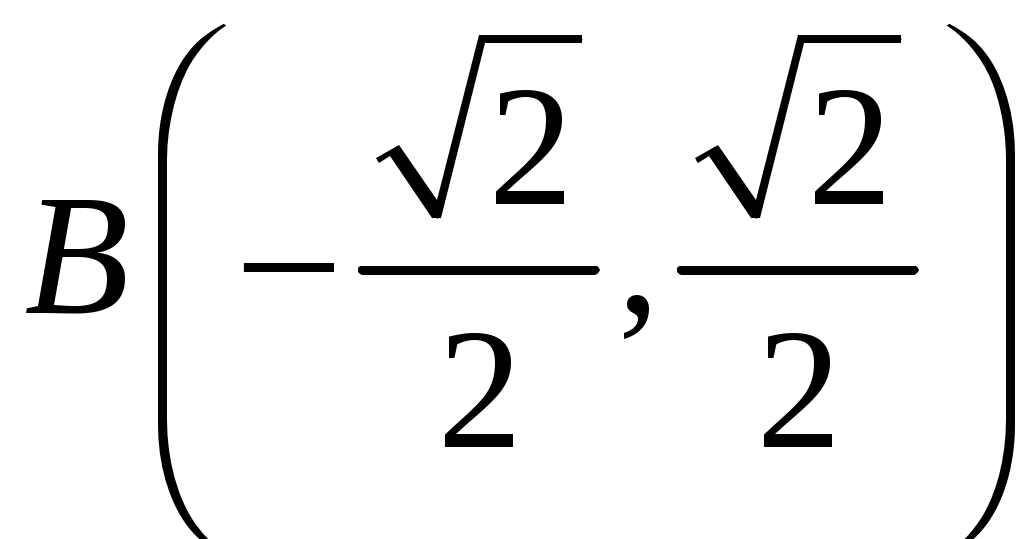.Решение: Зададим уравнение дуги
единичной окружности параметрически: 
, 
, 
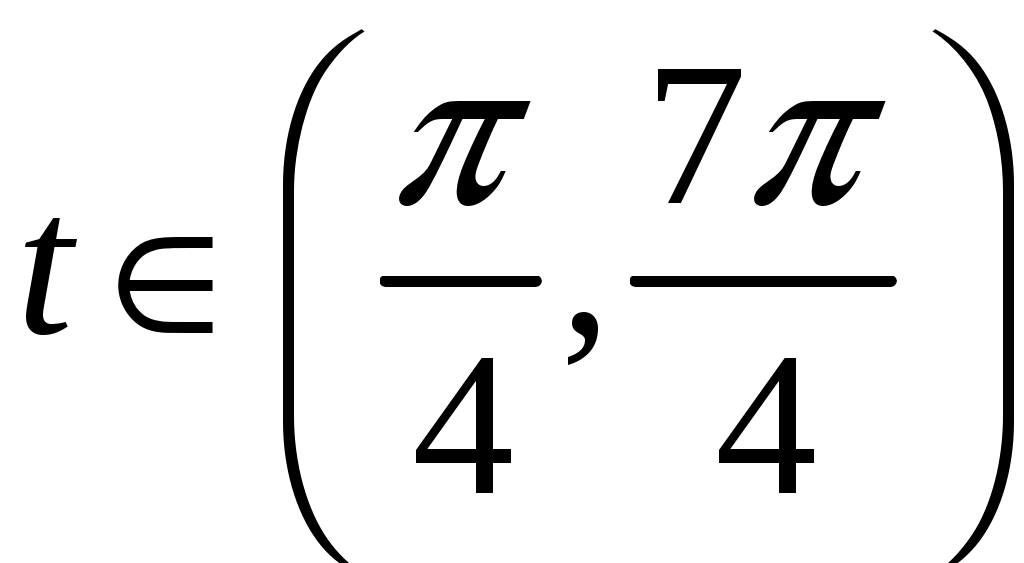. Ориентация дуги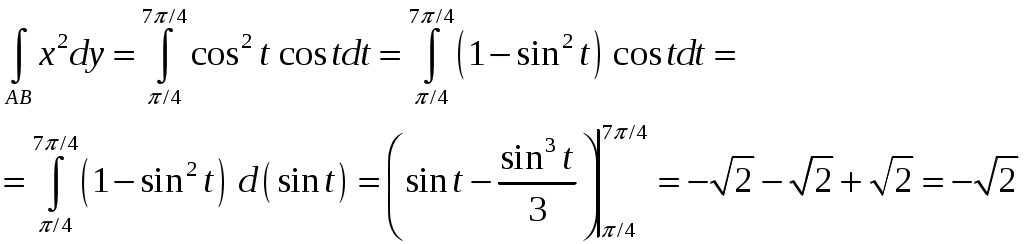 при этом будет удовлетворять условию задачи. Тогда по формуле вычисления криволинейного интеграла 2-рода имеем:
Задача №5
Вычислить криволинейный интеграл по окружности
, ориентированной по часовой стрелке:
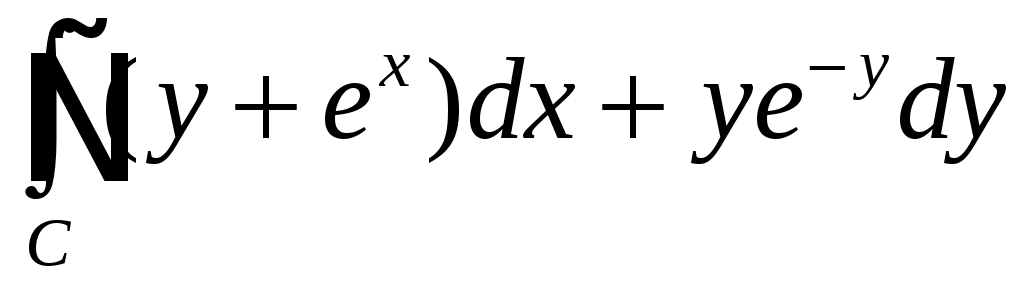.Решение
По формуле Грина, которая в данной задаче применима, т.к. кривая
кусочно-гладкая, а функции 
и 
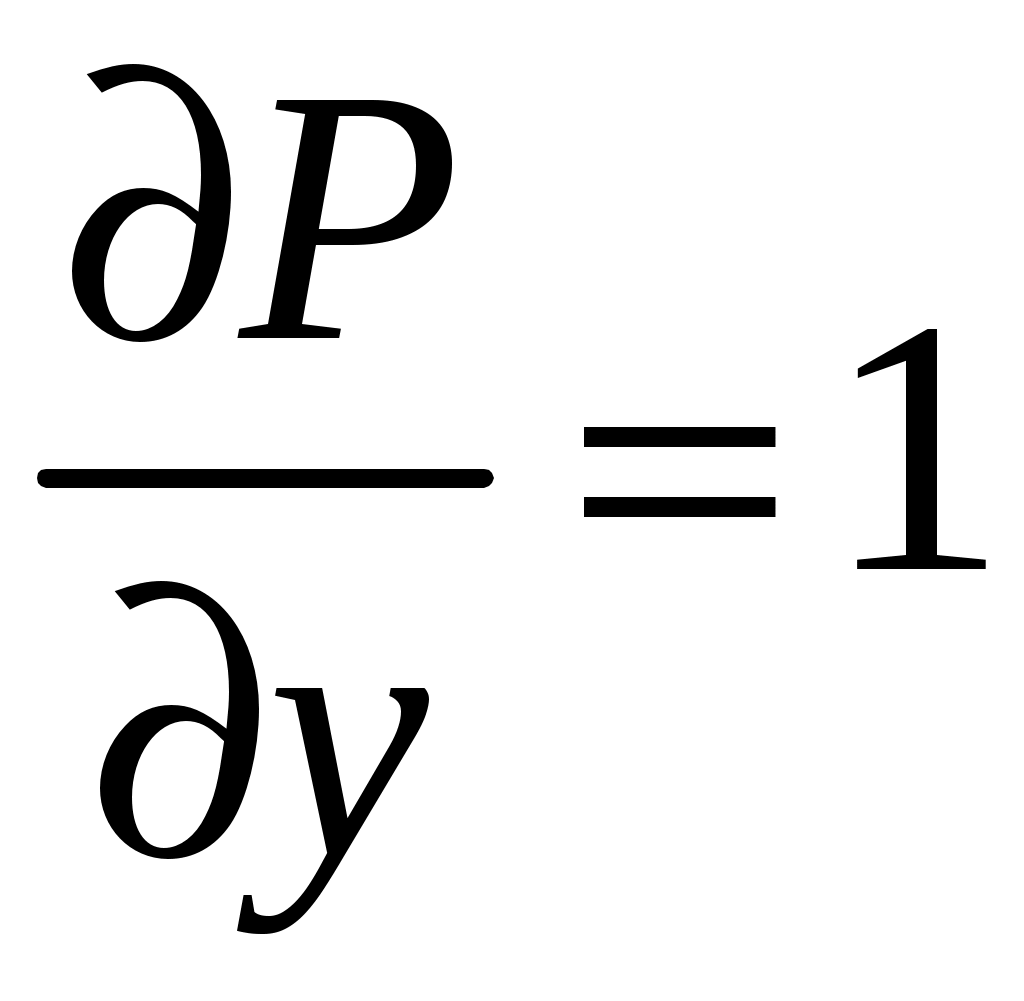– непрерывны вместе с частными производными 
и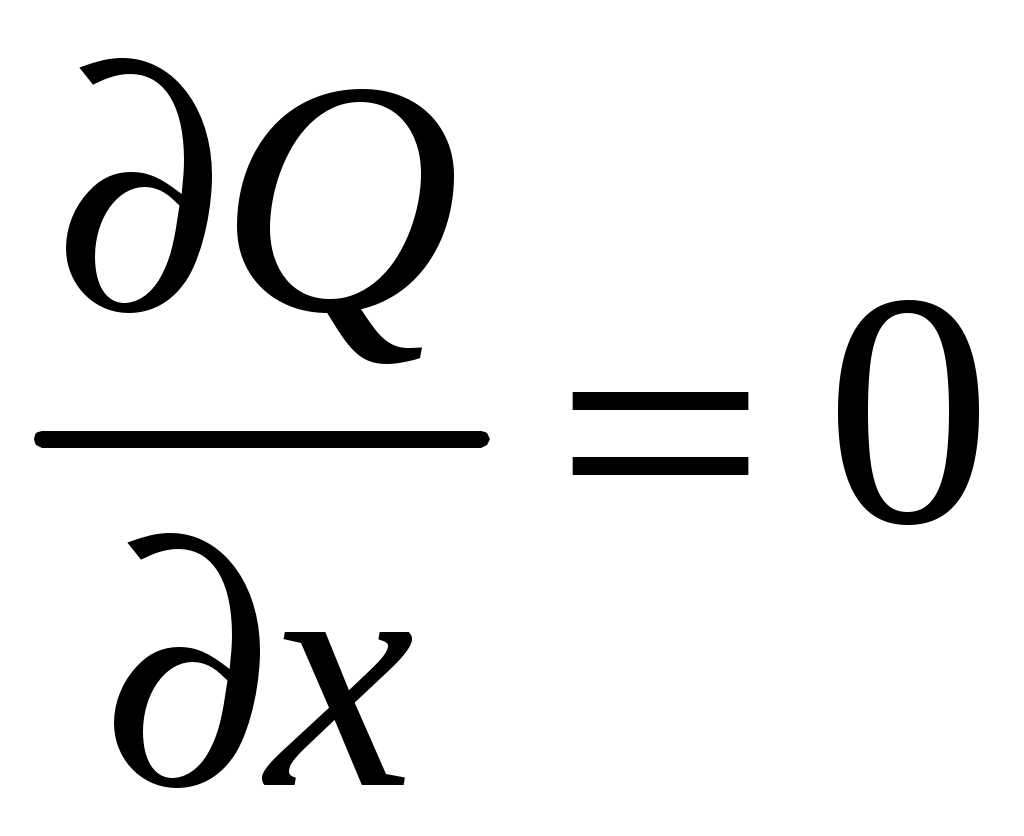 
в замкнутом круге 
: 
[1], имеем:
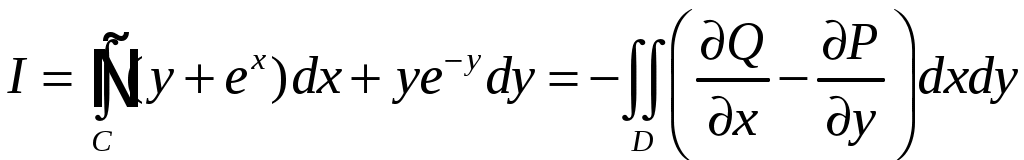,знак «–» перед двойным интегралом объясняется тем, что формула Грина верна при положительной ориентации границы области
, что в нашей задаче совпадает с ориентацией окружности
против часовой стрелки, а по условию надо подсчитать значение интеграла при противоположной ориентации окружности.
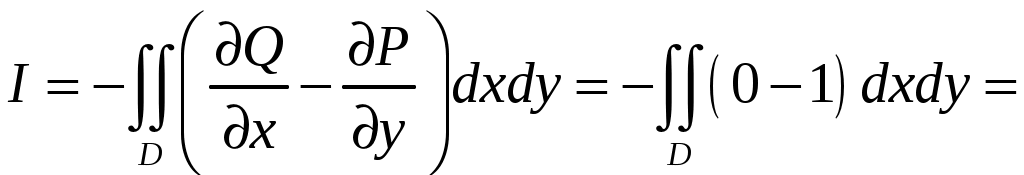
– площадь единичного круга.Задача №6
Вычислить поверхностный интеграл 2 рода по внутренней стороне сферы
:
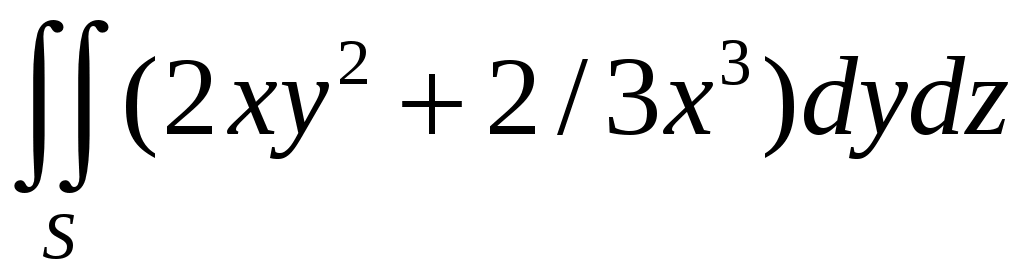.Решение
По формуле, задающей связь между поверхностным интегралами первого и второго рода [1], имеем:
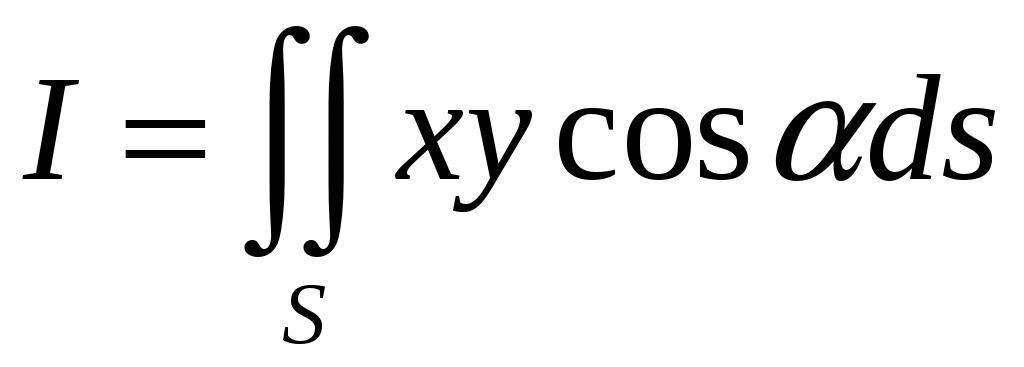,где
– косинус угла между единичной нормалью к сфере в заданной её точке и осью 
. По свойству сферы в нашей задаче 
, тогда
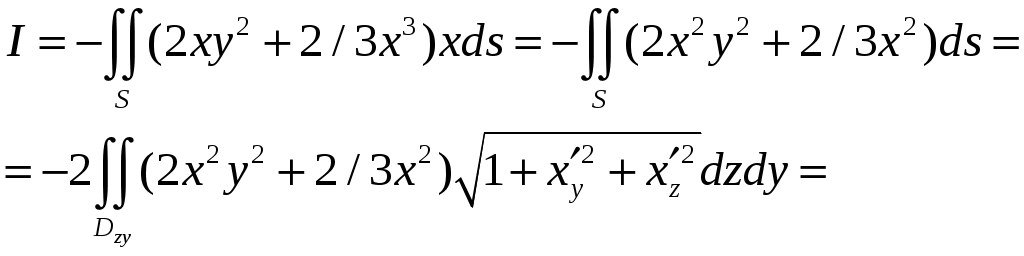
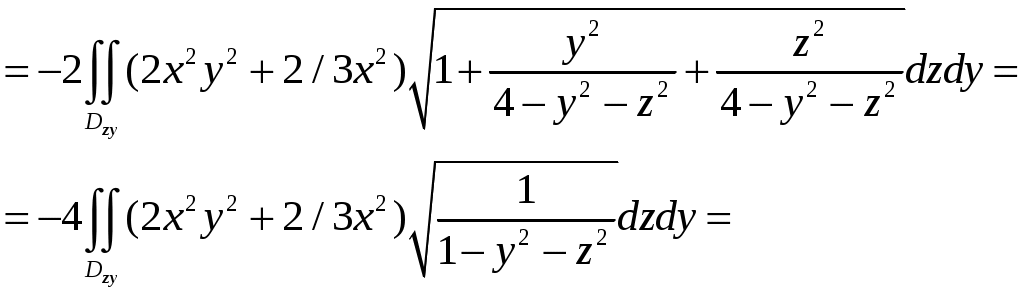
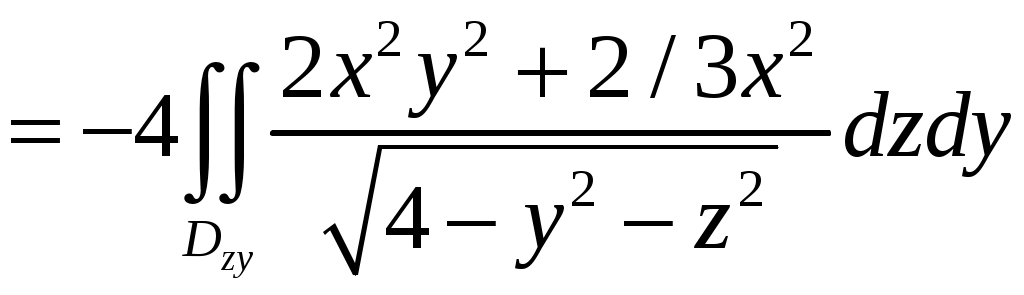,где
– уравнение сферы, 
– проекция двух полусфер 
и 
на плоскость 
.Тогда
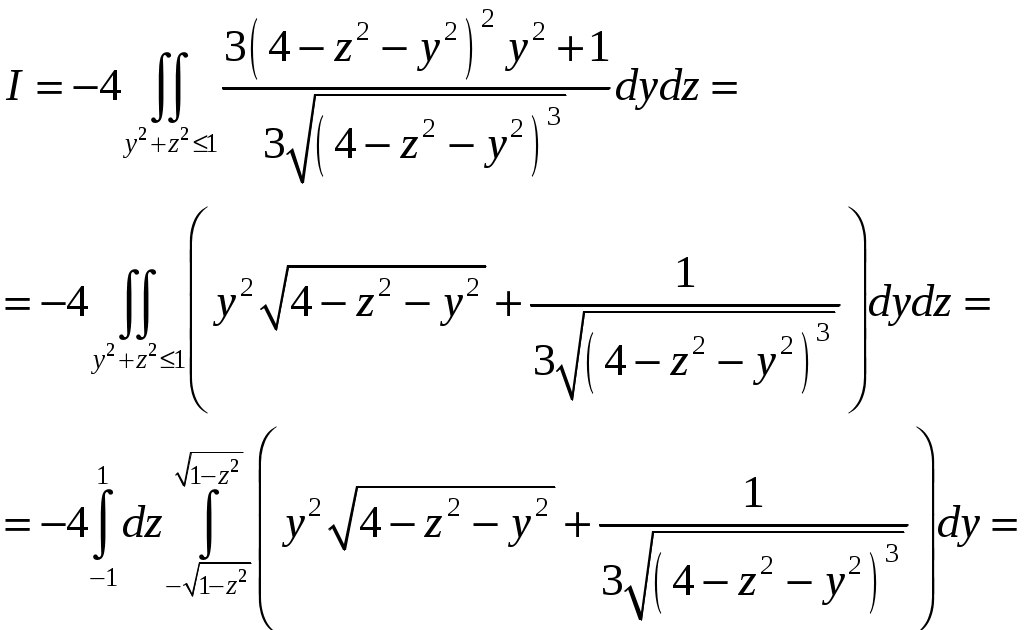
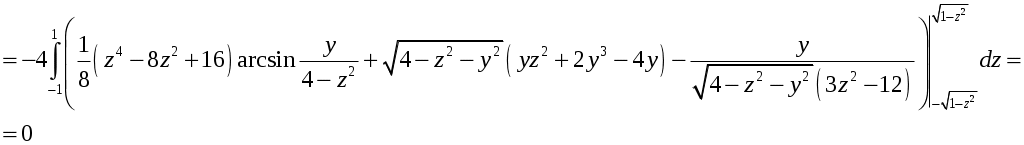
С другой стороны можно применить формулу Остроградского-Гаусса:
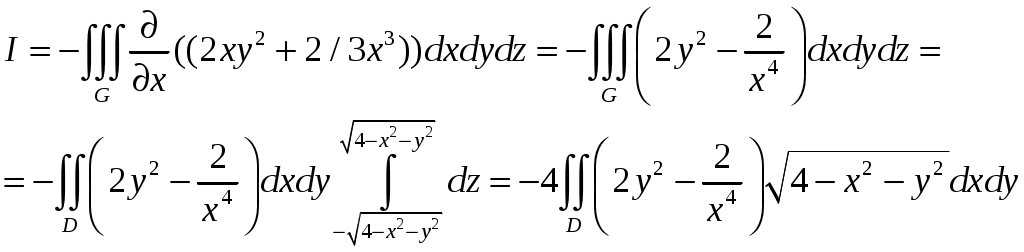, где 
– шар радиуса 2, 
– проекция шара на плоскость
. Последний интеграл совпадет с рассмотренным выше с точностью до обозначения переменных и, следовательно, также равен нулю.Задача №7
Найти общее решение дифференциального уравнения:
.Решение:
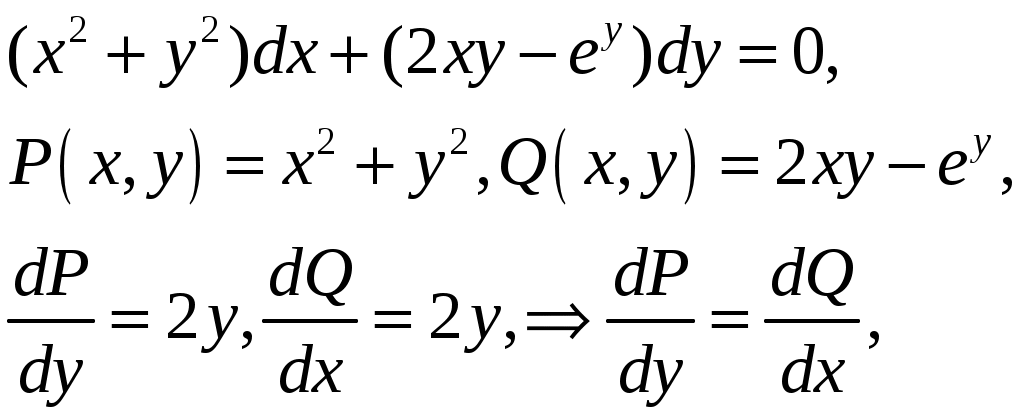
Имеем уравнение в полных дифференциалах, находим:
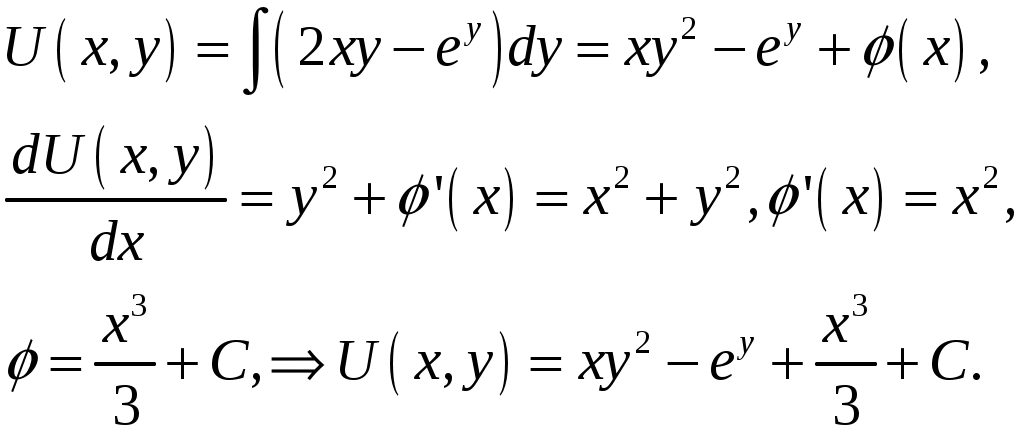
Задача №8
Найти решение дифференциального уравнения, удовлетворяющего начальному условию
: 
.Решение:
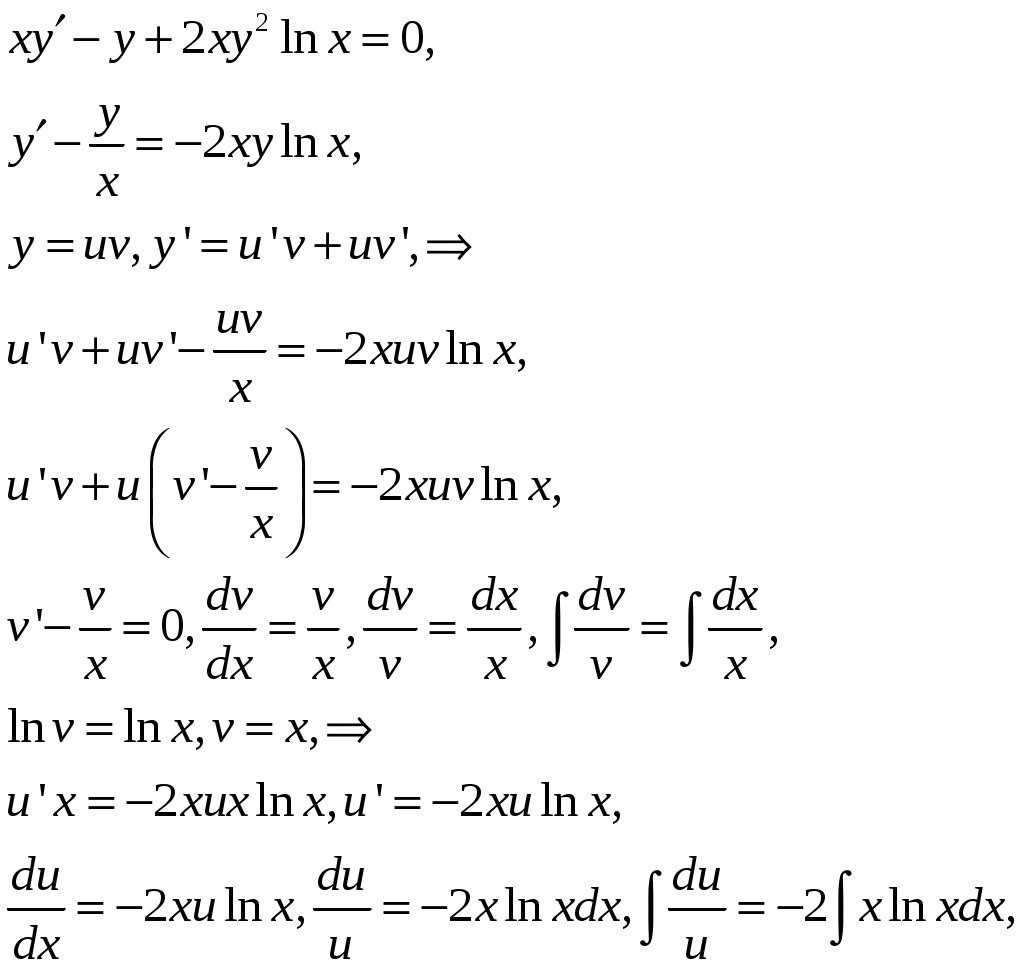
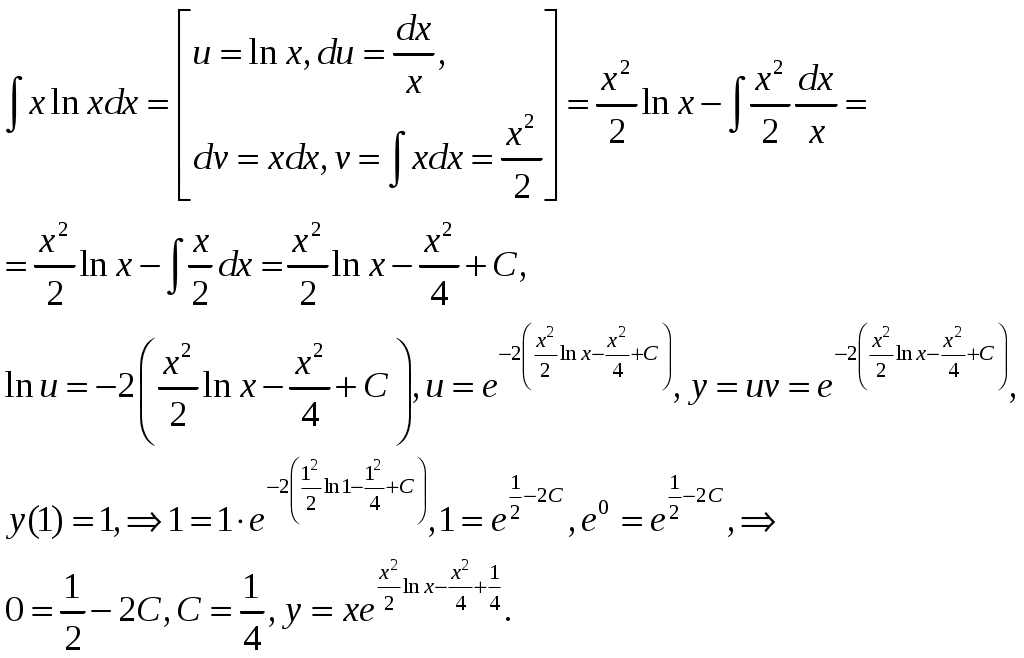
Задача №9
Решить задачу Коши:
, 
.Решение:
Уравнение не зависит от переменной
. Поэтому можно понизить порядок уравнения заменой 
, тогда 
.
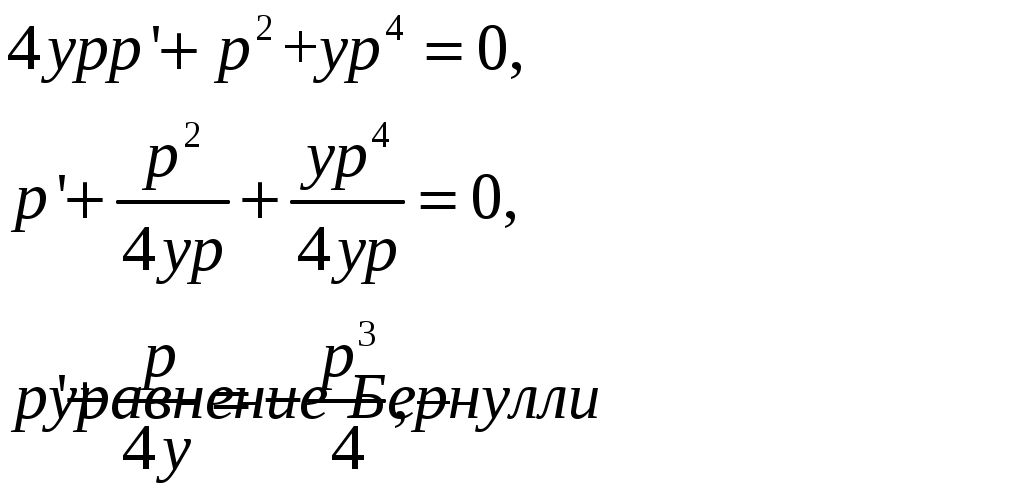
Решение будем искать в виде:
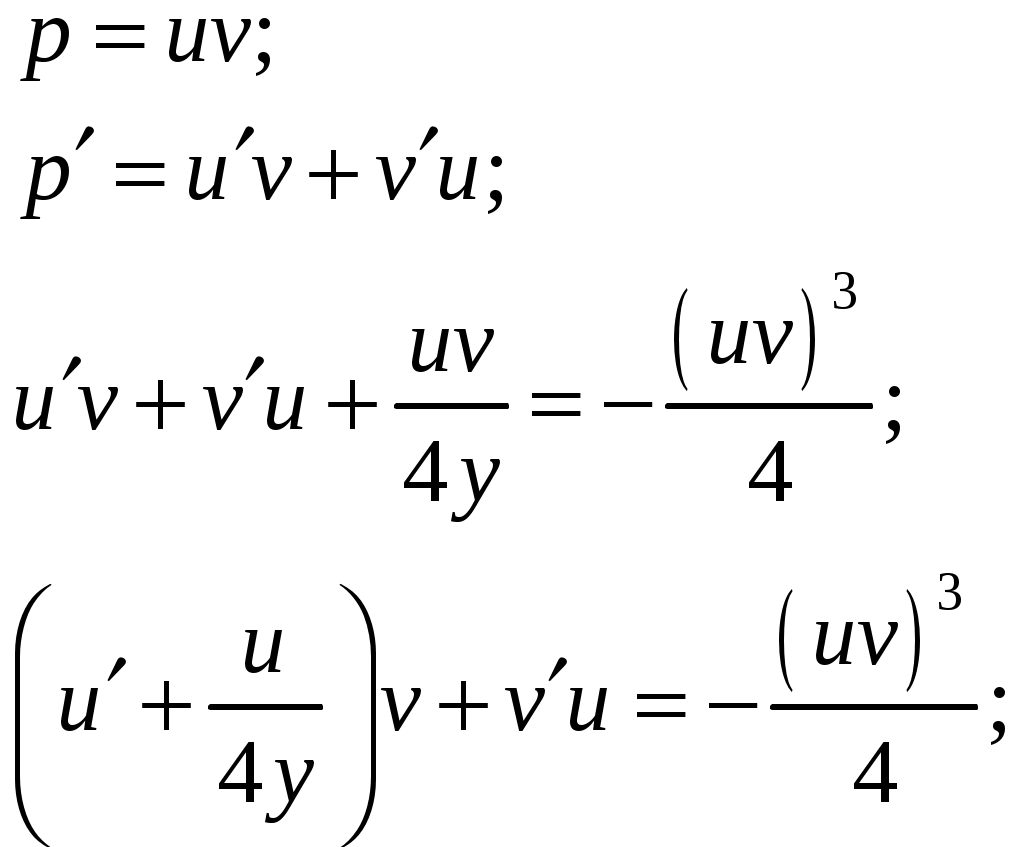
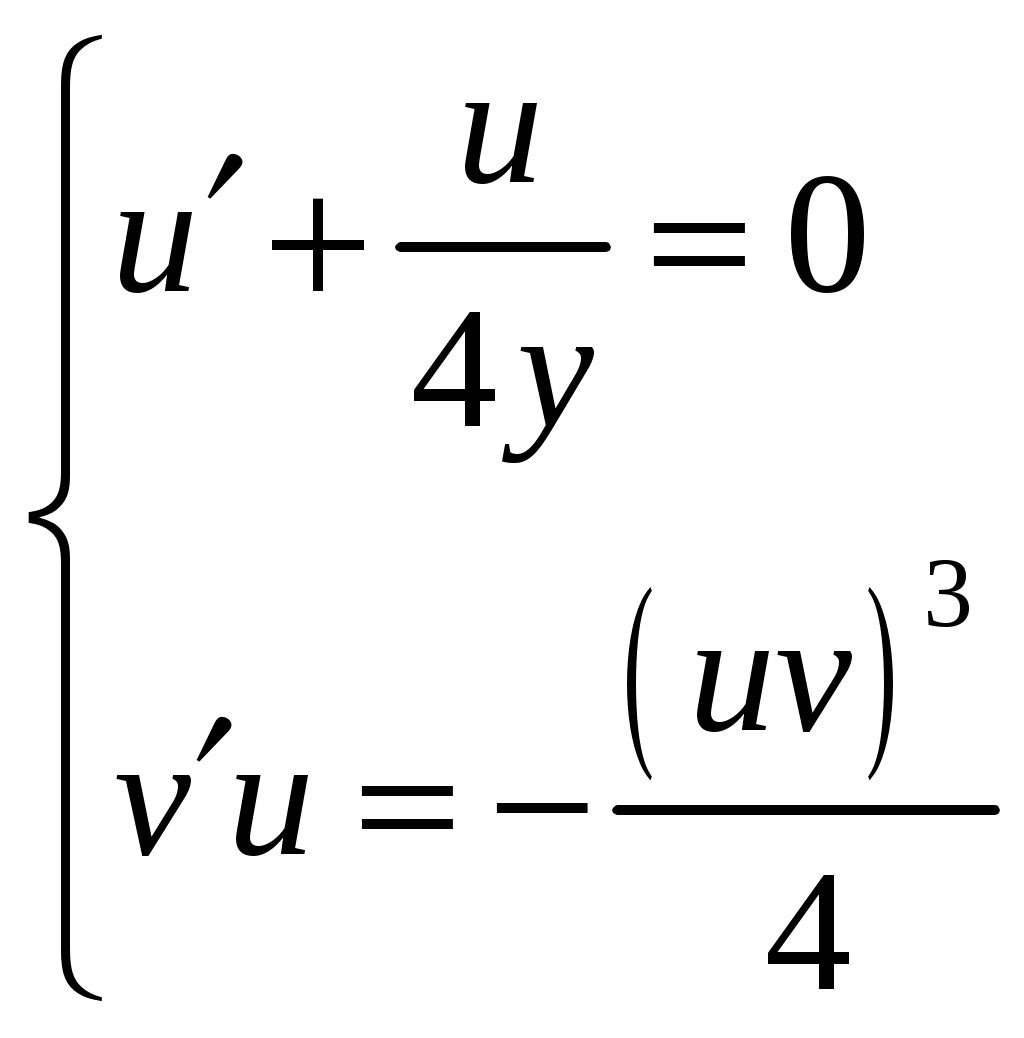
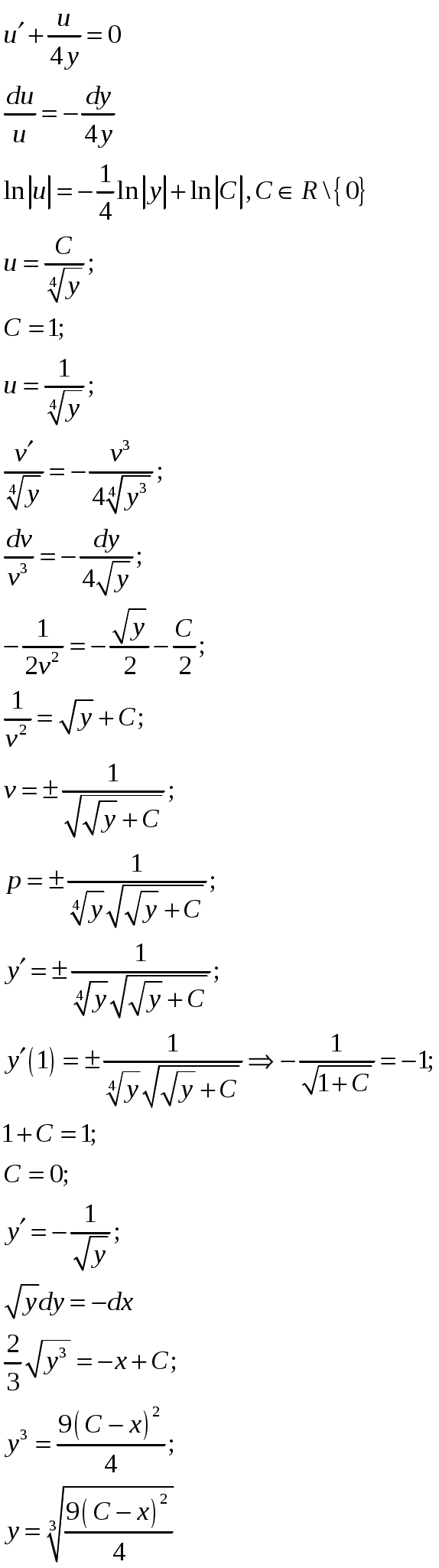
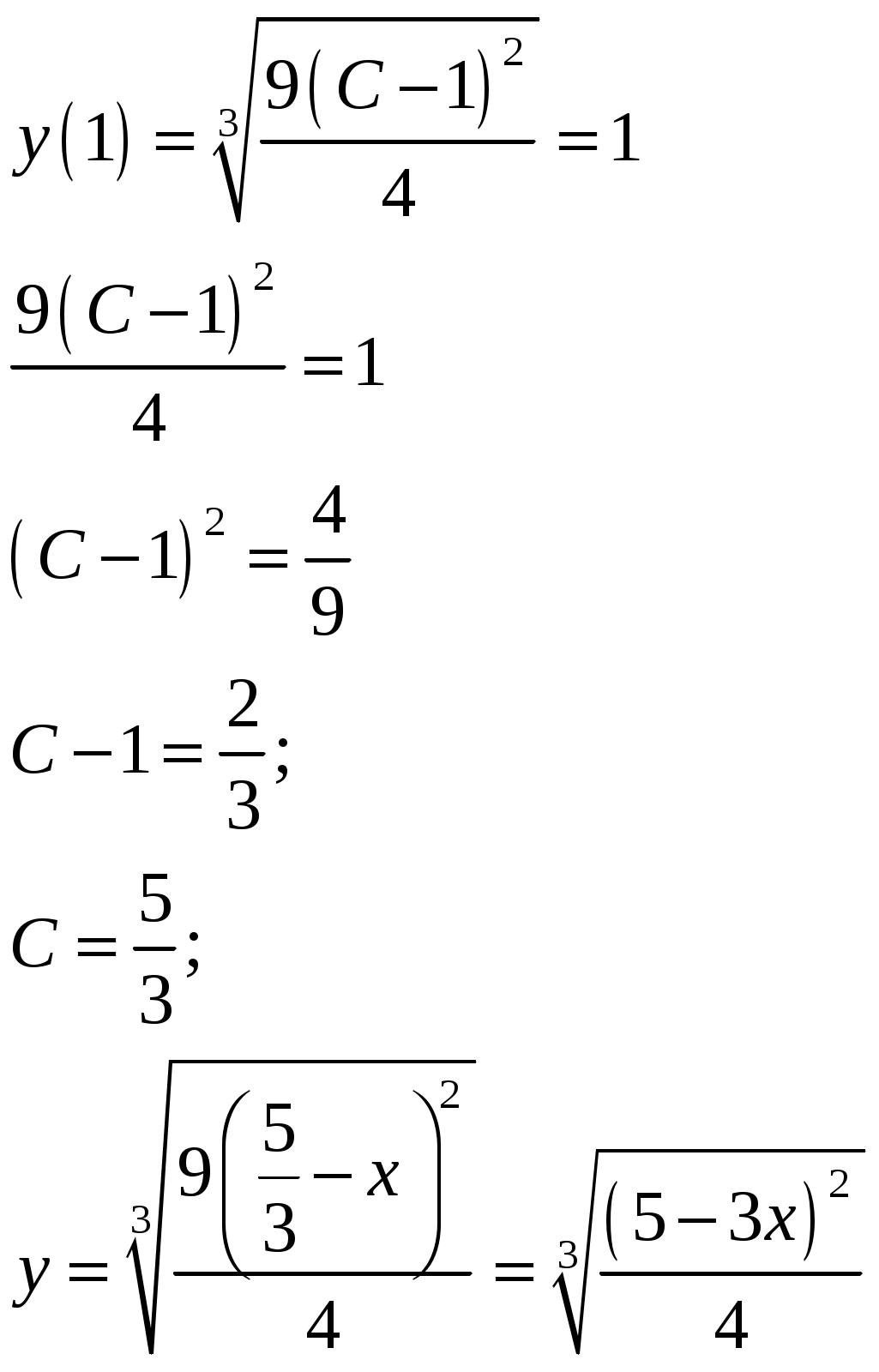
Задача №10
Найти общее действительное решение однородного дифференциального уравнения:
.
Решение:
Характеристическое уравнение:
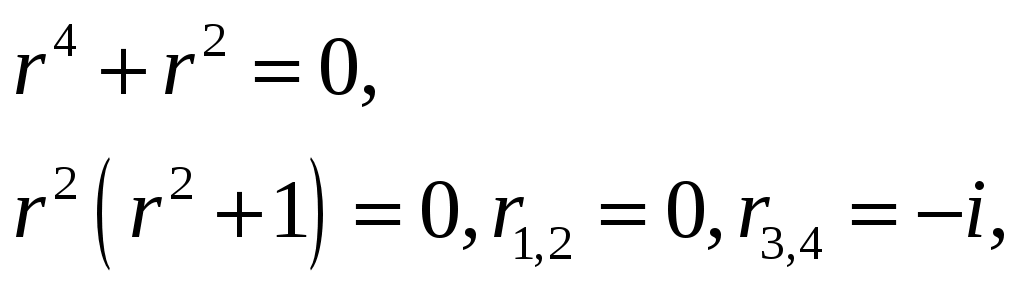
Общее решение однородного уравнения:
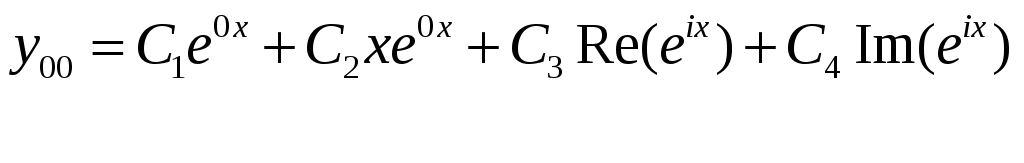
Т.к.
, 
, то общее действительное решение имеет вид: 
Задача №11
Два датчика посылают сигнал в общий канал связи, причем первый из них посылает вдвое больше сигналов, чем второй. Вероятность получить искаженный сигнал от первого датчика равна 0,06, от второго – 0,03. Какова вероятность получить искаженный сигнал в общем канале?
Решение:
Пусть х – количество сигналов второго датчика, 2ч-количество сигналов первого датчика, тогда:
P(A/H1)=0,01 - вероятность получить искаженный сигнал от 1
P(A/H2)=0,03 - вероятность получить искаженный сигнал от 2
P(H1)=2x/3x=2/3
P(H2)=1x/3x=1/3
По формуле полной вероятности, получаем:
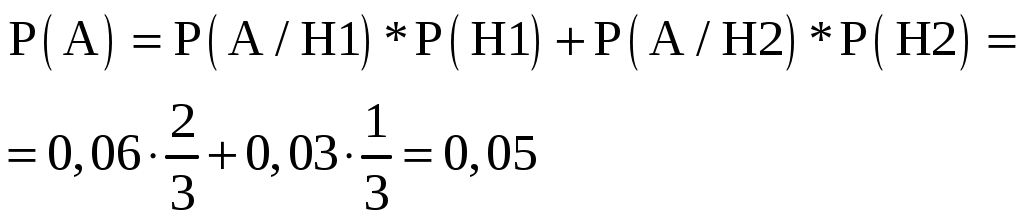
Задача №12
Семена содержат 0,1% сорняков. Оценить вероятность того, что при случайном отборе 10000 семян будет найдено от 10 до 13 сорняков.
Решение:
Применение локальной теоремы Лапласа, из-за малой вероятности р=0,001, приводит к значительному отклонению вероятности от точного значения
. Поэтому применяю асимптотическую формулу Пуассона:
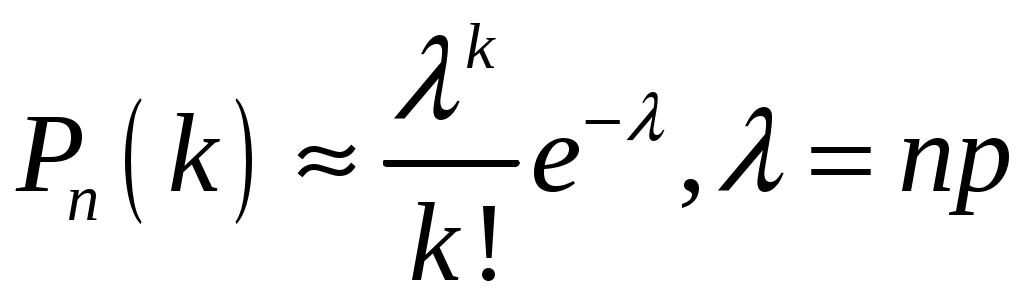
Эта формула используется при λ≤10. Чем меньше р и больше n, тем точнее результат. По условию задачи: р=0,001, n=10000,
. Тогда λ=10000·0,001=10,
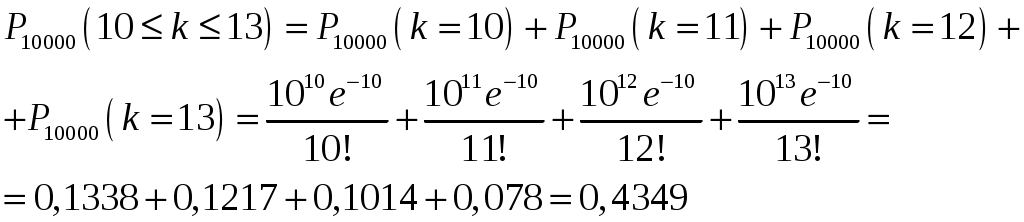
Задача №13
Случайная величина
