Файл: пензенский государственный университет политехнический институт.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Диссертация

Дисциплина: Не указана

Добавлен: 30.11.2023

Просмотров: 201

Скачиваний: 4

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Содержание

Введение

Основные положения, выносимые на защиту:

Эквивалентные преобразования моделей задач линейного программирования

Анализ моделей и алгоритмов решения задач о назначениях

Анализ эквивалентных преобразований моделей задач о назначениях

Выводы

Модель и алгоритм решения задачи с приоритетными назначениями

Выводы

Алгоритм решения простейшей линейной многокритериальной задачи о назначениях Многообразие многокритериальных задач в сочетании с отсутствием единого принципа оптимальности порождает огромное число методов их решению. Использование того или иного подхода к решению конкретной задачи может оказать существенное влияние на трудоемкость вычислений. Это относится особенно к специальным классам задач, для которых при скалярном критерии качества разработаны эффективные алгоритмы, использующие специфику ограничений и критериальной функции. Одной из таких задач является задача о назначениях.В основе подавляющего большинства методов решения многокритериальных задач лежит понятие веса критерия, характеризующего его сравнительную важность. Наиболее распространенные методы решения многокритериальных задач основаны на свертке набора исходных целевых функций (с учетом их веса) в один обобщенный скалярный критерий [71]. Такой подход позволяет получить оптимальное по Парето решение и при этом характеризуется вычислительной эффективностью. Использование свертки обеспечивает возможность применения для решения многокритериальной задачи о назначениях специально разработанные для однокритериального случая методы – венгерский и метод Мака.Свертка частных критериев разного смыслового содержания не позволяет интерпретировать значение взвешенного обобщенного критерия, поэтому в общем случае использование операторов свертки требует предварительного нормирования матриц затратСl,l 1, k, т.е. приведения их к единой безразмерной шкале. Часто используемый способ нормирования – минимакс-нормализация.Предлагается следующий алгоритм решения простейшей многокритериальной линейной задачи о назначениях (70) – (75). Нормировать матрицы затрат Сl, l 1, k: cl clсl ijmin . c  cijl maxlmin Составить целевые функции безразмерными коэффициентами: f1(X), f2 (X),..., fk(X) с n nlfl(X)  сijxij, l 1, ki1 j1 Составить вектор   (1, 2,..., k)весовых коэффициентов относительной важности целевых функцийf1(X), f2 (X),..., fk(X) ,l 0 , l 1.k, l 1. В том случае, если все критерии имеют одинаковуюl1 важность,l 1, l 1.k. Составить скалярную целевую функция (обобщенный критерий) g(X)   ) ,( f1(X), f2 (X),..., fk(X),где  – оператор свертки. Перейти к однокритериальной задаче о назначениях вида g(X)  min, (76) n xij 1, j 1, n,i1 (77) n xij 1, i 1, n,j1 (78) xij{0,1}, i, j 1, n. (79) Решить задачу (76) – (79) венгерским методом или методом Мака. Результатом является получение решения, оптимального по Парето. Решая задачу многократно и с изменением весовых коэффициентов, можно получить множество Парето-оптимальных решений. Вид свертки в каждом конкретном случае отражает приемлемую для ЛПР форму компромисса между частными критериями. Наиболее часто используемыми свертками являются линейная свертка, мультипликативная свертка и свертка на основе отклонения от идеальной точки. 1   ...   8   9   10   11   12   13   14   15   ...   21

Решение простейшей линейной многокритериальной задачи о назначениях с использованием свертки на основе отклонения от идеальной точки Под идеальной точкой в многокритериальной задаче о назначениях вида (71) – (76) понимают такой векторF*(X)  Rk, компоненты которого являются минимумами целевых функцийf1(X), f2 (X),..., fk(X) по отдельности, т.е.fl*(X)  min fl(X),XDl 1, k. В практических задачах идеальная точка является недостижимой [73]. Свертка на основе идеальной точкиF*(X)имеет вид: g(X)  (F(X), F*(X)) , где  – некоторая метрика вRk. Наиболее часто используются взвешенная чебышевская метрика g(X)  maxlfl(X)  fl* l (80) и взвешенная евклидова метрика kg(X)  ( fl(X)  fl*)2.l1 (81) Предлагается следующий алгоритм составления обобщенного скалярного критерия на основе идеальной точки: составить kоднокритериальных задач о назначениях вида n nlfl(X)  cijxij min,i1 j1n (82)  xij 1, j 1, n,i1n (83)  xij 1, i  1, n,j1 (84) xij{0,1}, i, j 1, n, (85) гдеl 1,k; найти X * – оптимальное решение l-й задачи вида (82) – (84) и lfl*  fl(X*) , l 1, k; lсоставить вектор F*(X)  ( f*, f*,..., f*) , гдеfl*  fl(X*) , l 1, k;1 2 k lсоставить свертку на основе отклонения от идеальной точки по формуле (80) или (81). Разработана программа для нахождения решения многокритериальной линейной задачи о назначениях с использованием свертки на основе отклонения от идеальной точки средствами математического пакета Mathcad, полный текст которой представлен в приложении E. На рисунке 20 приведены результаты применения свертки на основе отклонения от идеальной точки к многокритериальной задаче о назначениях, исходные данные которой совпадают с исходными данными задачи, решенной с использованием линейной свертки: Рисунок 20 – Результаты решения многокритериальной линейной задачи о назначениях с использованием свертки на основе отклонения от идеальной точки На рисунке 20 представлены матрица X – оптимальное по Парето решение, полученное с использованием чебышевской метрики, и матрица Y – оптимальное по Парето решение, полученное с использованием евклидовой метрики. Также программа находит для каждого оптимального по Парето решения значения соответствующего ему критериального вектора. Применяя алгоритм многократно с изменением весовых коэффициентов, можно построить множество точек Парето. Выбор конкретного решения из множества Парето-оптимальных осуществляется ЛПР.Следует отметить, что в некоторых прикладных задачах ЛПР за идеальную точку может принять реальное решение, соответствующее некоторым принятым стандартам или планируемым значениям. 1   ...   10   11   12   13   14   15   16   17   ...   21

Модель и алгоритм решения многокритериальной задачи о назначениях с целевыми функциями противоположного направления

Модель и алгоритм решения многокритериальной открытой задачи о назначениях Обобщим открытую задачу о назначениях на случай многокритериальности. Математическая модель такой задачи в предположенииm nимеет вид:

Модель и алгоритм решения многокритериальной задачи с порядком назначений Обобщим задачу с порядком назначений на случай многокритериальности. Математическая модель такой задачи имеет вид:nn f1(X)  c1 x min,(121) ijiji1 j1… nn k(X)  ckx min,n (122)  xij 1,n j 1, n, (123)  xij 1, i  1, n, (124) {0,1}, i1, n, j 1, n, , i1, n, j h1, n, j*  1, h. (126) f xij гдеP {1,2,.., h}пр.(i, j)  (i, j*)– подмножество индексов работ, распределяемых в первую очередь.В главе 2 показано, что однокритериальная задача с порядком назначений эквивалента совокупности двух последовательно решаемых задач – открытой и с недопустимыми назначениями. Аналогично, многокритериальная задача с порядком назначений эквивалента совокупности двух последовательно решаемых задач – многокритериальной открытой задаче и многокритериальной задаче с недопустимыми назначениями. Следовательно, можно описать алгоритм решения многокритериальной задачи с порядком назначений. Нормировать матрицы затрат Сl, l 1, k: cl clсl ijmin . c  cijl maxlmin Найти размер штрафа Ml 2n. Построить математическую модель назначения на работы из множества P :

Выводы

Заключение

Список использованных источников






Решение простейшей линейной задачи о назначениях в пакете

«Mathcad» осуществляется с помощью встроенной функции «Minimize», возвращающей матрицу искомых значений неизвестных, при которых исследуемая целевая функция имеет минимальное значение. При использовании функции «Minimize» автоматически определяется тип задачи математического программирования (линейная или нелинейная) и подбирается подходящий алгоритм оптимизации из группы доступных методов. Если задача линейная, как в приведенном случае, то применяется симплекс-метод. Результаты работы программы приведены на рисунке 1:



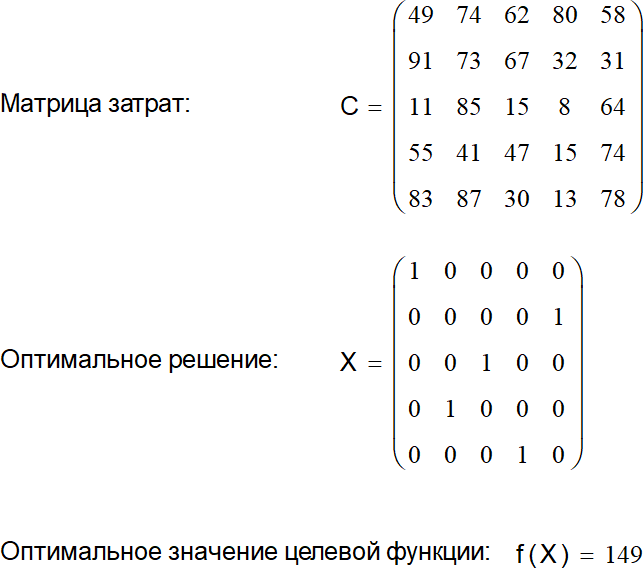
Рисунок 1 – Исходные данные и решение простейшей линейной задачи о назначениях
Достоинствами приведенного способа решения простейшей линейной задачи о назначениях является наглядность и несложность программирования при увеличении размерности задачи.
    1. 1   2   3   4   5   6   7   8   9   ...   21

Анализ моделей и алгоритмов решения задач о назначениях



Как правило, большинство модификаций и обобщений простейшей линейной задачи о назначениях вытекают из практических нужд. Следствием прикладной направленности задачи является многообразие ее моделей. Различные виды моделей задач о назначениях можно классифицировать по ряду признаков (рисунок 2).






Интервальные ЗОН
ЗОН на максимум
Нелинейные ЗОН
Числовые ЗОН

По направлению оптимизации
По виду целевой функции


По размерности неизвестных



Многокритериальные ЗОН

По количеству целевых функций
По мощности множеств индексов



По типу коэффициентов целевой функции






ЗОН с минимаксным критерием


Нечеткие ЗОН


Закрытые


ЗОН с максиминным критерием


Многоиндексные ЗОН


Рисунок 2 – Классификация задач о назначениях
По виду целевой функции можно выделить два основных класса задач:

  • линейные задачи о назначениях;

  • нелинейные задачи о назначениях.

Задача о назначениях с линейной целевой функцией широко применяется во многих областях практической деятельности и имеет множество интерпретаций: подбор кадрового персонала и трудоустройство населения [3, 4], отбор контрагентов на конкурсной основе [5, 6], раcпределение продавцов по торговым точкам [7], назначение транспорта на маршруты [8] и пр. Наиболее изученной является простейшая линейная задача, определяемая соотношениями (1) – (4), для которой разработаны многочисленные точные алгоритмы решения.

Среди нелинейных задач весьма широкие области приложения имеет класс задач с квадратичной целевой функцией. В одной из частых постановок она рассматривается как задача о размещении производственных объектов по локациям [9]. Для каждой пары локаций задано расстояние, для каждой пары производственных объектов задан вес или поток (например, количество продукции, перевозимой между двумя производствами). Требуется расставить производства по локациям таким образом, что сумма расстояний, умноженных на соответствующие потоки, будет минимальной, при этом два производства

нельзя размещать в одном месте. Задачи о назначениях с квадратичной целевой функцией возникают при проектировании и оптимизации логистической системы предприятий, размещении вычислительных задач в узлах распределенной вычислительной среды, проектировании генеральных планов предприятий, расчете оптимального расположения технологического оборудования в цехах и т.д.

Квадратичная задача о назначениях относится к классу NP-полных задач. Для точного решения задачи применяются модифицированные методы комбинаторного анализа и целочисленного программирования [10, 11, 12]. Разработан ряд эвристических алгоритмов, позволяющих найти субоптимальное решение, например, алгоритм «табу-поиска» [13, 14], итеративный локальный поиск [15, 16, 17], Для поиска решения часто используются генетические алгоритмы [18, 19, 20], муравьиный алгоритм [21, 22], алгоритмы на основе нейронных сетей [23]. Многие исследования связаны с разработкой алгоритмов решения квадратичной задачи о назначениях на графах и сетях. Постановка в терминах теории графов удобна, когда специфика прикладной задачи предполагает наличие специальных структур связей между объектами [24]. Показано, что если графы связей и расстояний являются изоморфными деревьями, то квадратичная задача о назначениях разрешима за полиномиальное время алгоритмом динамического программирования [10]. В [25] предложен алгоритм локальной оптимизации для задачи о назначениях на двудольных графах. В [26, 27] предложен ряд полиномиальных алгоритмов решения квадратичной задачи о назначениях для специальных видов графов и сетей. В частности, рассматривается размещение цепи и цикла на древовидной взвешенной сети. В [24] предложен параллельный алгоритм динамического программирования решения квадратичной задачи о назначениях с минисуммным критерием для графа связей общей структуры с произвольными весами ребер на древовидной сети с равными весами. Дальнейшее обобщение вида целевых функций приводит к кубическим и биквадратным (четвертые степени) задачам о назначениях [28, 29].

По направлению оптимизации можно выделить следующие классы задач:


  • задачи о назначениях с целевой функцией на минимум;

  • задачи о назначениях с целевой функцией на максимум;

  • задача о назначениях с минимаксным критерием;

  • задача о назначениях с максиминным критерием.

Направление оптимизации целевой функции зависит от того, что понимается под эффективностью выполнения работ в той или иной задаче. Во многих случаях, в том числе и в простейшей линейной постановке, задача о назначениях заключается в распределении работ по исполнителям с целью минимизации суммарных затрат. Если же эффективность выполнения работ оценивается приносимой прибылью, то за целевую функцию принимается суммарная прибыль, которую следует максимизировать. Обычно решение такой задачи основывается на переходе к матрице, эквивалентной исходной, коэффициенты которой имеют смысл потерь прибыли от максимально возможной и дальнейшей минимизации потери прибыли [30, 31].

Минимаксный критерий возникает, когда важно минимизировать максимальное из значений потерь [10]. Алгоритм решения минимаксной задачи, описанный в [32], представляет собой модификацию алгоритма Дейкстры. В [33] предложен алгоритм решения минимаксной задачи о назначениях на графах, который в случае открытой минимаксной задачи о назначениях является полиномиальным. В [34] описан алгоритм решения минимаксной задачи высокой размерности, результатом применения которого является получение множества решений, оптимальных по Парето. В [35] предложены использующие многокритериальные схемы компромисса алгоритмы решения максиминной задачи о назначениях.

По типу коэффициентов целевой функции можно выделить следующие классы задач:

  • детерминированные задачи о назначениях, в которых коэффициенты целевой функции являются числами;

  • интервальные задачи о назначениях, в которых коэффициенты целевой функции заданы числовыми интервалами;

  • нечеткие задачи о назначениях, в которых коэффициенты целевой функции являются нечетким числами (интервалами).

Подавляющее большинство задач о назначениях содержат целевую функцию с числовыми коэффициентами. Между тем, на практике встречаются такие задачи, коэффициенты целевых функции которых известны лишь с той или иной степенью неопределенности. Здесь возникают интервальные и нечеткие задачи о назначениях. В связи с естественной множественностью неточно поставленных целей, для таких задач нет единого подхода в определении понятия оптимальности решения, что обусловливает многообразие алгоритмов решения [36 – 42]. При этом наиболее часто используется детерминизационный подход к оптимизации интервальных или нечетко определенных функций.

По количеству целевых функций можно выделить:

  • однокритериальные задачи о назначениях;

  • многокритериальные задачи о назначениях.

Многокритериальность часто возникает при формализации различных прикладных проблем. Так, в [43] описана многокритериальная постановка задачи о назначениях на предфрактальном графе, формализующая задачу конкурсного отбора проектов со сложными связями между заказчиками и исполнителями, и предложен алгоритм выделения совершенного паросочетания. В [44] задача составления расписания учебных занятий с учетом дополнительных требований рассматривается как многокритериальная задача о назначениях. Для поиска решения такой задачи используется генетический алгоритм. В [45] представлена двухкритериальная модель задачи о назначениях с формализованным дополнительным требованием учета предпочтений соискателя вакансии при подборе места работы. Алгоритм решения такой задачи основан на использовании метода гарантированного результата с последующим переходом к двойственной задаче и применением алгоритма Удзавы.

Многие работы посвящены обоснованию используемой схемы компромисса [35, 46, 47, 48, 49]. Например, в [50] для определения назначе- ний при оперативном планировании в редакционном отделе крупного издательства с учетом интересов членов коллектива в качестве критерия решения задачи рассматривается выбор наиболее близких по своим векторным характеристикам пар «объект – субъект». Также известны работы, связанные с проблемой нормирования критериев [51].

Смотрите также файлы