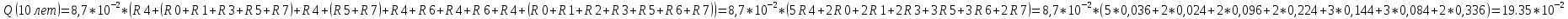Добавлен: 01.12.2023
Просмотров: 127
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
1.Особенности надёжности и безопасности СЖАТ
2.Показатели надёжности для невосстанавливаемых и восстанавливаемых систем
3.Методы расчёта показателей надёжности СЖАТ
3.1 Статистические оценки показателей надежности.
3.1.1 Построение функции распределения и функции плотности распределения по статистической выборке
3.1.2 Статистическая оценка параметров надежности восстанавливаемых устройств
3.2 Расчет надежности комбинационных схем
3.3 Расчет показателей надёжности восстанавливаемых систем методом Марковских процессов
3.4 Структурный метод расчёта надёжности
3.5 Топологический метод расчета надежности резервированных систем
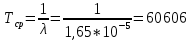
Данные для построения кривой на графике зависимости частоты отказов от количества:
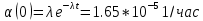
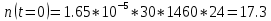
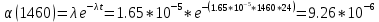
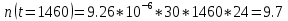
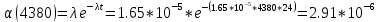
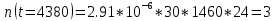
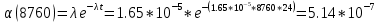
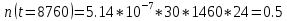
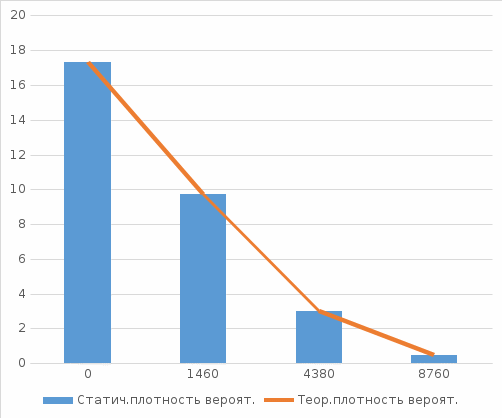
Рис.1 Гистограмма с нанесенной теоретической функцией частоты отказов
3.1.2 Статистическая оценка параметров надежности восстанавливаемых устройств

Рис.2.
Рисунок 2 – Заданный промежуток времени
Исходные данные, согласно варианту, приведены в таблице 2.
Таблица 2
| t1, мес | t2, мес | t3, мес | N0, шт | n01, шт | n12, шт | n23, шт | nв01, шт | nв12, шт | nв23, шт |
| 26 | 52 | 78 | 2600 | 78 | 78 | 104 | 52 | 78 | 104 |
Заданный промежуток Δ12=
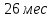 . За этот промежуток сгорело n02=78 лампочек, успели восстановить nв02=78 лампочек.
. За этот промежуток сгорело n02=78 лампочек, успели восстановить nв02=78 лампочек. Вероятность отказа:
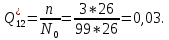
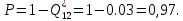
Частоту отказов можно найти по формуле:
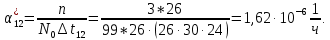
Интенсивность отказов находим по формуле:
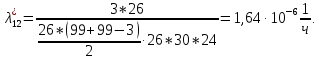
Среднее время наработки на отказ:
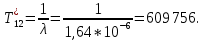
Далее найдем показатели ремонтопригодности.
Вероятность восстановления находим по формуле:
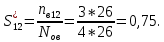
При этом считаем, что число, поставленных на восстановление устройств на начало промежутка N0В, равно числу неисправных устройств на всем рассматриваемом промежутке.
Частоту восстановления и интенсивность восстановления найдем по формуле:
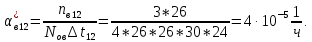
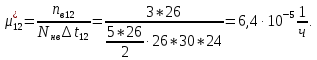
Коэффициент готовности:
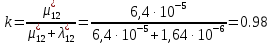
3.2 Расчет надежности комбинационных схем
Логическая функция в алгебраическом виде:
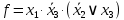
Используя правила синтеза, построим комбинационную схему на двухвходовых логических элементах:
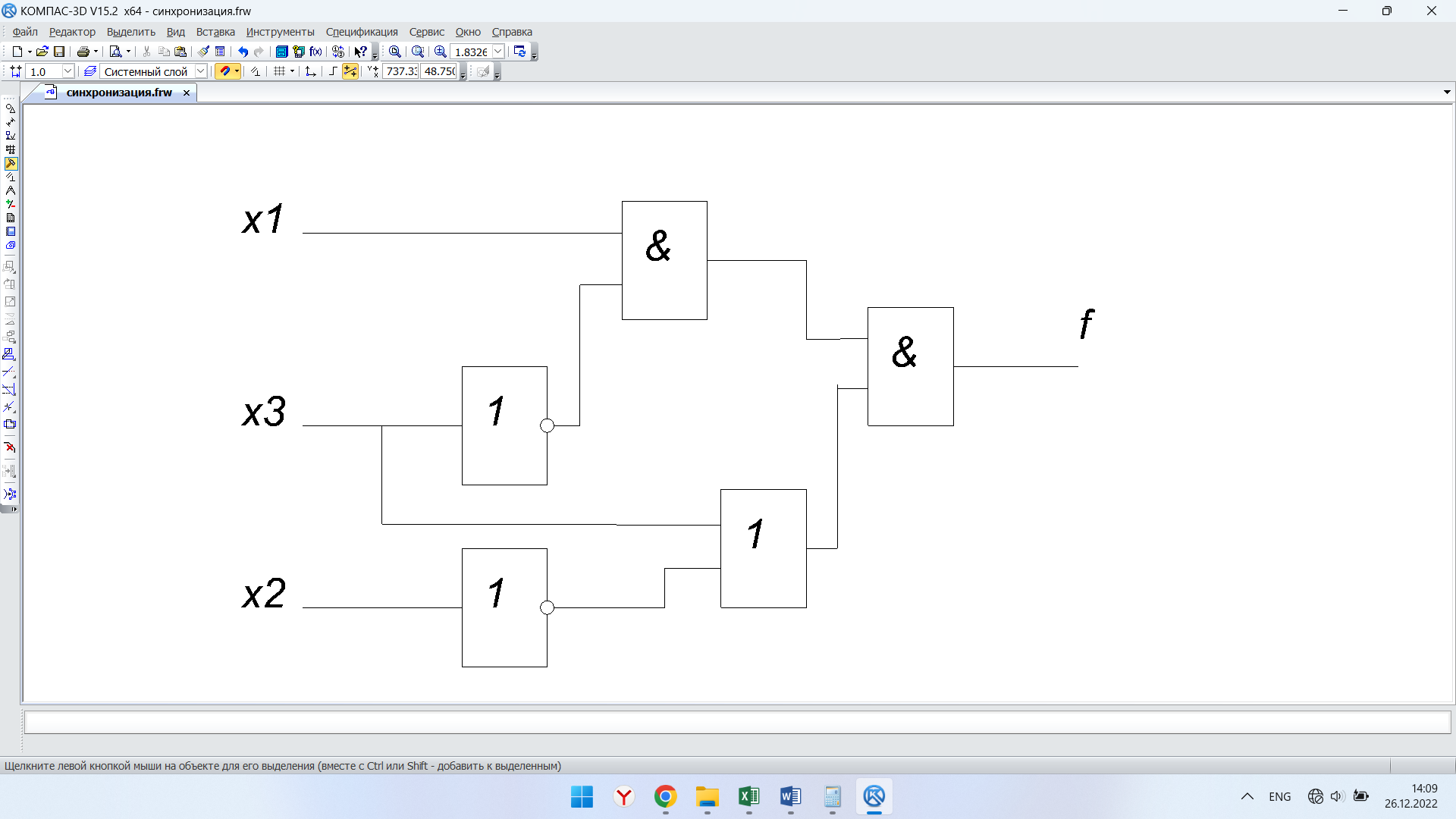
Рис.3. Комбинационная схема на логических элементах
Рассмотрим неисправности на выходе всех логических элементов, входящих в схему:
Таблица 3
| S | 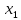 | 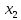 | 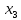 |  |  | 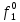 | 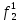 | 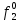 | 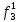 | 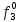 | 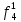 | 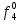 | 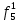 | 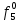 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 3 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 4 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 5 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 6 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 7 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| S |  |  |  |  | 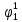 | 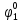 | 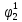 | 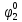 | 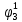 | 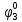 | 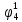 | 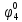 | 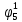 | 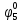 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 3 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 4 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 5 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 6 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 7 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
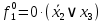
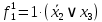
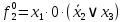
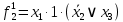
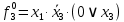
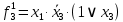
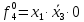
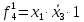
Вероятности появления входных переменных ????1= 0,6; ????2= 0,7; ????3= 0,8.
Определим вероятности Rk появления входных наборов и составим таблицу, отражающую полную группу событий на входе схемы:
Таблица 4
| S | X1 | X2 | X3 | f | Rk |
| 0 | 0 | 0 | 0 | 0 | R0=(1-0,6)*(1-0,7)*(1-0,8)=0,024 |
| 1 | 0 | 0 | 1 | 0 | R1=0,4*0,*0,8=0,096 |
| 2 | 0 | 1 | 0 | 0 | R2=0,4*0,7*0,2=0,056 |
| 3 | 0 | 1 | 1 | 0 | R3=0,4*0,7*0,8=0,324 |
| 4 | 1 | 0 | 0 | 1 | R4=0,6*0,3*0,2=0.036 |
| 5 | 1 | 0 | 1 | 0 | R5=0,6*0,3*0,8=0,144 |
| 6 | 1 | 1 | 1 | 0 | R6=0,084 |
| 7 | 1 | 1 | 1 | 0 | R7=0,336 |