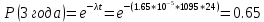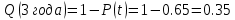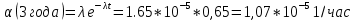Файл: Методы расчета показателей надежности сжат.docx

При разработке и обслуживании в процессе эксплуатации систем автоматики, телемеханики и связи инженер должен обеспечивать выполнение алгоритма функционирования и определённый уровень надёжности.

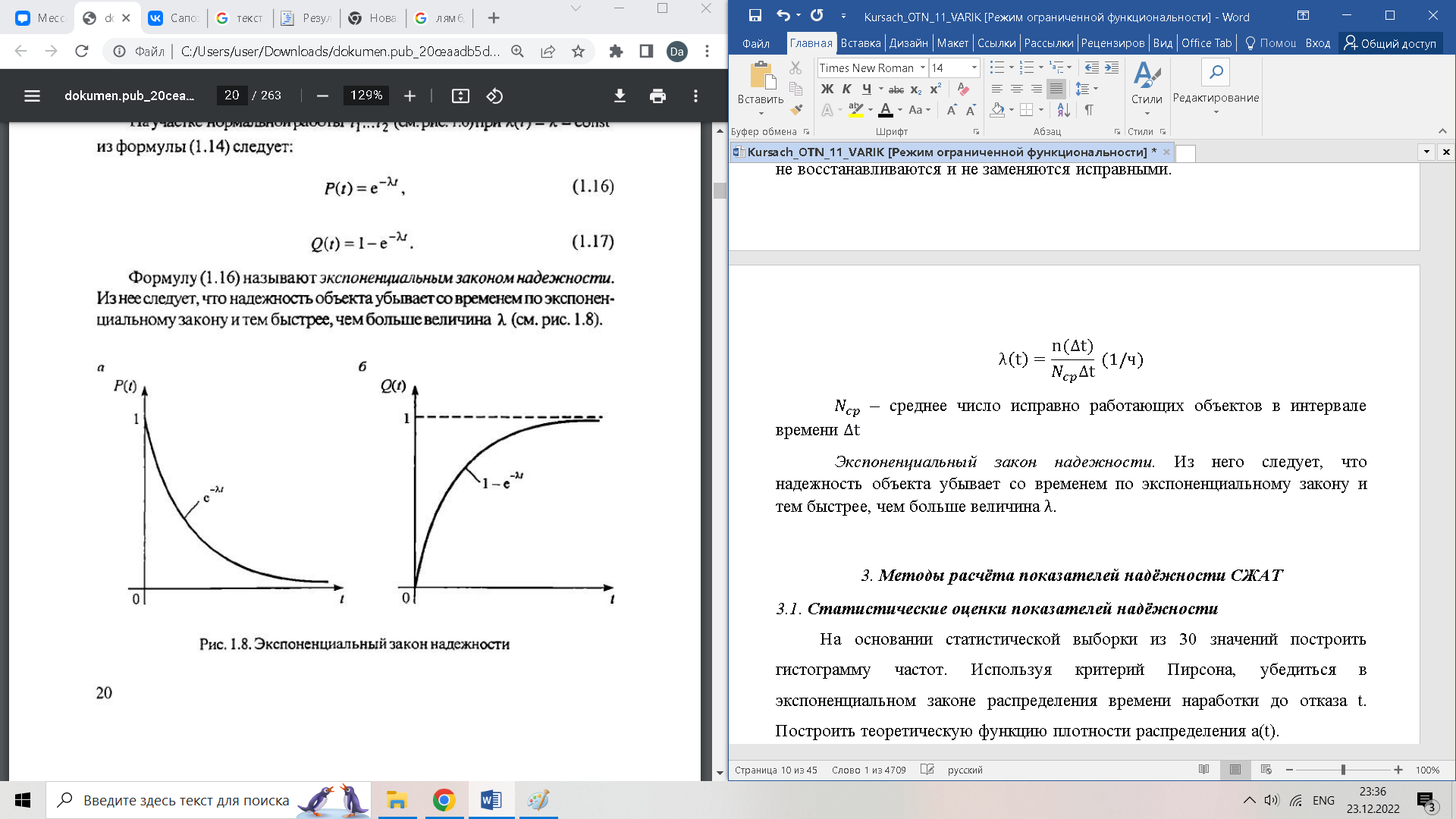
Надёжность важнейшая характеристика любого технического объекта, от которой зависит целесообразность его использования по назначению. При разработке и внедрении новой аппаратуры обычно определяют показатели её надёжности.

Надежность – свойство объекта сохранять во времени в установленных пределах значения всех параметров, характеризующих способность выполнять требуемые функции в заданных режимах и условиях применения, технического обслуживания, ремонта, хранения и транспортирования.

Надёжность объекта оценивается не только во время непосредственной эксплуатации, но и во время хранения, транспортировки и ремонта. Поэтому надёжность является сложным свойством и состоит из сочетания следующих свойств: безотказности, долговечности, ремонтопригодности и сохраняемости.

Надежность связана со всеми этапами проектирования, изготовления и использования изделия. Каждый из этих этапов вносит свою лепту в решение трудной задачи создание изделия требуемого уровня надёжности с наименьшими затратами времени и средств. При проектировании и расчёте изделия закладывается его надёжность. Она зависит от конструкции, применяемых материалов, методов защиты от различных вредных воздействий, системы смазки, приспособленности к ремонтам и обслуживанию и других конструктивных особенностей.

При изготовлении изделия обеспечивается его надёжность. Она зависит от качества изготовленных деталей, методов контроля выпускаемой продукции, возможностей управления ходом технологического процесса, от качества сборки изделия и его узлов, методов испытания готовой продукции и других показателей технологического процесса.

2.Показатели надёжности для невосстанавливаемых и восстанавливаемых систем

Невосстанавливаемые системы

Пусть некоторый исправный объект начинает работать в момент времени t=0, а в момент времени t происходит его первый отказ. Время t от начала эксплуатации до возникновения первого отказа называется наработкой до отказа. Наработка до отказа есть случайная величина.

---

Функцию распределения наработки до отказа Q(t) называют вероятностью отказа. Таким образом, Q(t) есть вероятность того, что наработка до отказа меньше t, или вероятность того, что за время t объект откажет. Основным показателем безотказности является вероятность безотказной работы Р(t) -вероятность того, что в пределах заданной наработки t отказ объекта не возникает (ГОСТ 27.002—89). Исправная работа и отказ в течение времени t являются несовместными событиями. Поэтому

Р(t)+ Q(t) =1

Функция Р(t) имеет следующие свойства:

1) Р(0) =1(это означает, что в начальный момент времени объект считается работоспособным);

2) 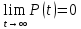(объект не может сохранять работоспособность неограниченно долго);

3) ;

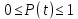4) 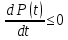(функция Р(t) является убывающей и истечением времени надежность невосстанавливаемого объекта не может возрастать).

Плотность распределения наработки до отказа называют частотой отказов:



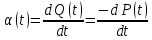
Интенсивностью отказов называется отношение числа отказавших объектов в единицу времени к среднему числу объектов, исправно работающих в данный отрезок времени при условии, что отказавшие объекты не восстанавливаются и не заменяются исправными.



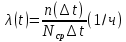
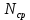– среднее число исправно работающих объектов в интервале времени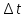

Экспоненциальный закон надежности. Из него следует, что надежность объекта убывает со временем по экспоненциальному закону и тем быстрее, чем больше величина .



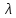Восстанавливаемые системы

Время эксплуатации восстанавливаемого объекта состоит из интервалов времени работы 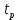, и интервалов времени восстановления

---

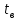, которые следуют друг за другом. Величины , , 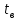и проявляются случайными. Поэтому показатели надежности делятся на три группы: показатели безотказности (характеризуют время ), показатели ремонтопригодности (характеризуют время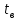 ) и комплексные показатели (характеризуют одновременно безотказность и ремонтопригодность).

В пределах отдельного интервала работы для восстанавливаемого объекта справедливы все показатели безотказности, рассмотренные в предыдущем разделе [Р(t), Q(t), 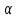(t), (t)] , если считать за начальный момент времени (t = 0) начало интервала.

Чтобы учесть факт отказа и восстановления объекта, вводят параметр потока отказов 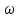(t) — отношение среднего числа отказов восстанавливаемого, объекта за произвольно малую его наработку к значению этой наработки: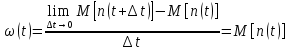


Где 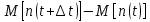– математическое ожидание отказов за время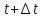

Статистически параметр потока отказов



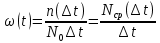
Средняя наработка на отказ



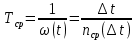
Этот показатель характеризует среднее время между соседними отказами восстанавливаемого объекта

Вероятность восстановления работоспособного состояния S(t)- вероятность того, что время восстановления работоспособного состояния объекта не превысит заданного времени t





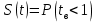
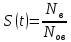
Где 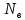-число объектов, восстановленных за время t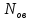

---

- число объектов, поставленных на восстановление

Частота восстановления



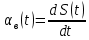
Интенсивность восстановления



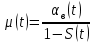
Коэффициент готовности



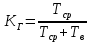
Коэффициент готовности – комплексный показатель надежности, который учитывает безотказность и ремонтопригодность объекта.

---

3.Методы расчёта показателей надёжности СЖАТ

3.1 Статистические оценки показателей надежности.

3.1.1 Построение функции распределения и функции плотности распределения по статистической выборке

Построение функции распределения и функции плотности распределения по статистической выборке.

Количество попаданий в интервалы. Таблица 1

ti	120	254	407	416	441	703	781	813	900	971	1152	1155	1225	1234	1375
К	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
ti	1379	1393	1505	1434	1839	2416	2531	3229	3674	4537	5216	8504	8692	8703	8703
К	1	1	2	2	2	2	2	3	3	4	4	6	6	6	6

Количество интервалов К:



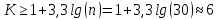
Интервалы :



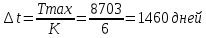
Находим n_i(∆t_i):

n1=6; n2=2; n3=1; n4=1.

Найдем показатели надежности за 1 год:

---