Добавлен: 03.12.2023
Просмотров: 62
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство цифрового развития и массовых коммуникаций
Российской Федерации
Ордена Трудового Красного Знамени федеральное государственное
бюджетное образовательное учреждение
высшего образования
«Московский технический университет связи и информатики»
(МТУСИ)
Кафедра Информатики
Отчет по лабораторной работе №4
по дисциплине «МЛиТА»
на тему:
«Минимизация логических выражений»
Выполнил: студент группы БСТ2205
Чёрный Станислав Дмитриевич
Вариант 14
Проверил:
Семин Валерий Григорьевич
Москва 2023
1 Задание
Написать минимальное выражение для заданной таблицы истинности и нарисовать по нему логическую схему.

Запишем минимальное выражение для заданной таблицы истинности посредством карт Карно.
-
Запись данных в таблицу
Таблица 2 – Составление карты Карно
 x3x4 x3x4x1x2 | 00 | 01 | 11 | 10 |
| 00 | f(0000) | f(0001) | f(0011) | f(0010) |
| 01 | f(0100) | f(0101) | f(0111) | f(0110) |
| 11 | f(1100) | f(1101) | f(1111) | f(1110) |
| 10 | f(1000) | f(1001) | f(1011) | f(1010) |
-
Составление Карты Карно
 x3x4 x3x4x1x2 | 00 | 01 | 11 | 10 |
| 00 | 0 | 1 | 1 | 1 |
| 01 | 0 | 0 | 1 | 1 |
| 11 | 1 | 1 | 0 | 0 |
| 10 | 1 | 0 | 1 | 0 |
-
Сцепление единиц
1 группа
 x3x4 x3x4x1x2 | 00 | 01 | 11 | 10 |
| 00 | 0 | 1 | 1 | 1 |
| 01 | 0 | 0 | 1 | 1 |
| 11 | 1 | 1 | 0 | 0 |
| 10 | 1 | 0 | 1 | 0 |
2 группа
 x3x4 x3x4x1x2 | 00 | 01 | 11 | 10 |
| 00 | 0 | 1 | 1 | 1 |
| 01 | 0 | 0 | 1 | 1 |
| 11 | 1 | 1 | 0 | 0 |
| 10 | 1 | 0 | 1 | 0 |
3 группа
 x3x4 x3x4x1x2 | 00 | 01 | 11 | 10 |
| 00 | 0 | 1 | 1 | 1 |
| 01 | 0 | 0 | 1 | 1 |
| 11 | 1 | 1 | 0 | 0 |
| 10 | 1 | 0 | 1 | 0 |
4 группа
 x3x4 x3x4x1x2 | 00 | 01 | 11 | 10 |
| 00 | 0 | 1 | 1 | 1 |
| 01 | 0 | 0 | 1 | 1 |
| 11 | 1 | 1 | 0 | 0 |
| 10 | 1 | 0 | 1 | 0 |
5 группа
 x3x4 x3x4x1x2 | 00 | 01 | 11 | 10 |
| 00 | 0 | 1 | 1 | 1 |
| 01 | 0 | 0 | 1 | 1 |
| 11 | 1 | 1 | 0 | 0 |
| 10 | 1 | 0 | 1 | 0 |
-
Считывание
1 группа: Объединяются ячейки с координатами 0011, 0010, 0111 и 0110. Следует взять
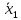 и
и 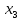 , а
, а 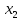 и
и 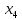 исключить, так как их значение изменяются и, следовательно, исчезают.
исключить, так как их значение изменяются и, следовательно, исчезают. Ответом будет являться –
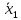
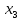 .
. 2 группа: Объединяются ячейки с координатами 1100 и 1101. Следует взять
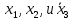 , а
, а 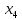 исключить, так как его значение изменяется и, следовательно, исчезает.
исключить, так как его значение изменяется и, следовательно, исчезает.
Ответом будет -
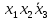 .
.3 группа: Объединяются ячейки с координатами 0001 и 0011. Следует взять
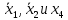 , а
, а  исключить, так как его значение изменяется и, следовательно, исчезает.
исключить, так как его значение изменяется и, следовательно, исчезает. Ответом будет -
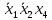 .
.4 группа: Объединяются ячейки с координатами 1011 и 0011. Следует взять
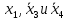 , а
, а  исключить, так как его значение изменяется и, следовательно, исчезает.
исключить, так как его значение изменяется и, следовательно, исчезает. Ответом будет -
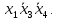
5 группа: Объединяются ячейки с координатами 1100 и 1000. Следует взять
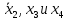 , а
, а 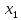 исключить, так как его значение изменяется и, следовательно, исчезает.
исключить, так как его значение изменяется и, следовательно, исчезает. Ответом будет -
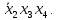
-
Составим МСДНФ
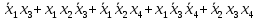
-
Реализуем схему функции на логических элементах
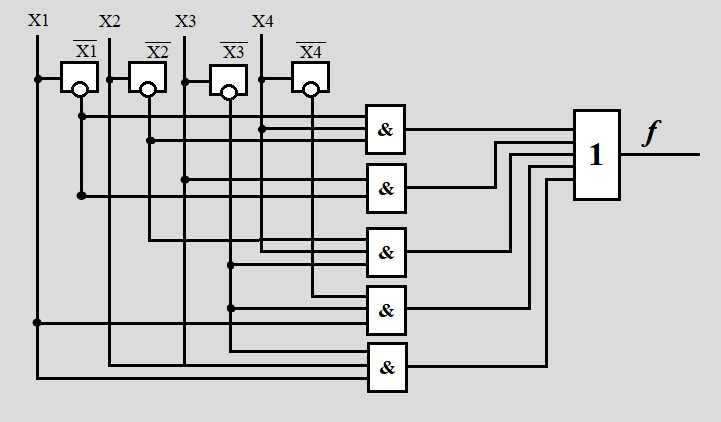
Рисунок 1 – Схема в базисе ИЛИ-НЕ
2 Задание
Для заданного логического выражения написать каноническую сумму минтермов и нарисовать минимальную логическую схему.
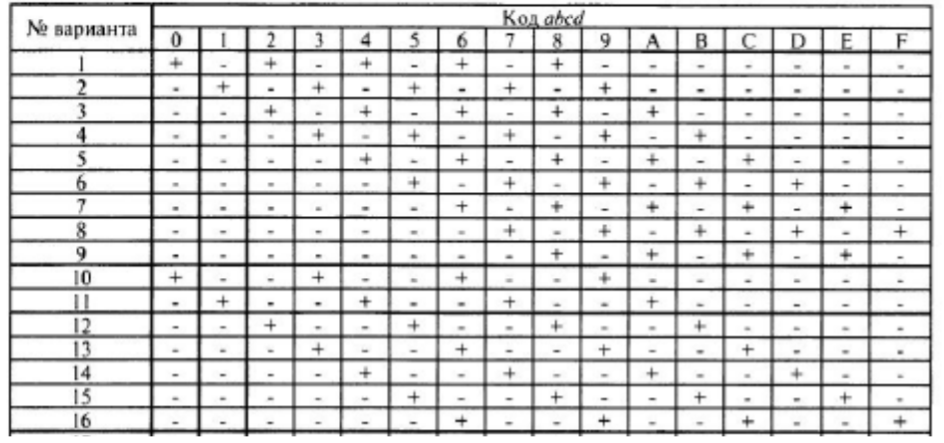
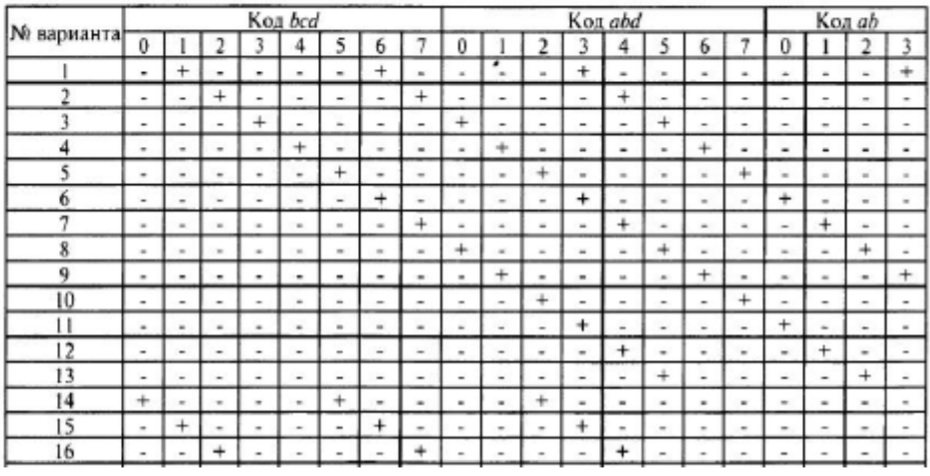
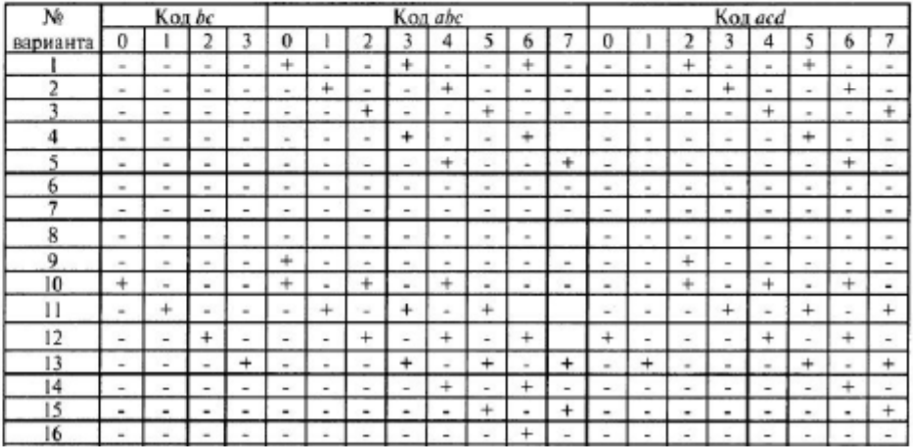
КСМ для первой таблицы
В первой таблице 14 варианта стоят плюсы под числами 4, 7, A, D.
Кодом всех этих чисел является код abcd. Следовательно, каждое число необходимо представить в виде тетрад в двоичной ССЧ и далее преобразовать числа так, как описано в 1 пункте. Полученные минтермы:
-
4 = 0100 =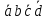 ;
; -
7 = 0111 =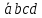 ;
; -
A = 1010 =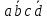 ;
; -
D = 1101 =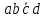 .
.
Каноническая сумма минтермов:
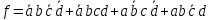
Минимальная логическая схема для первой таблицы представлена на рисунке 2.
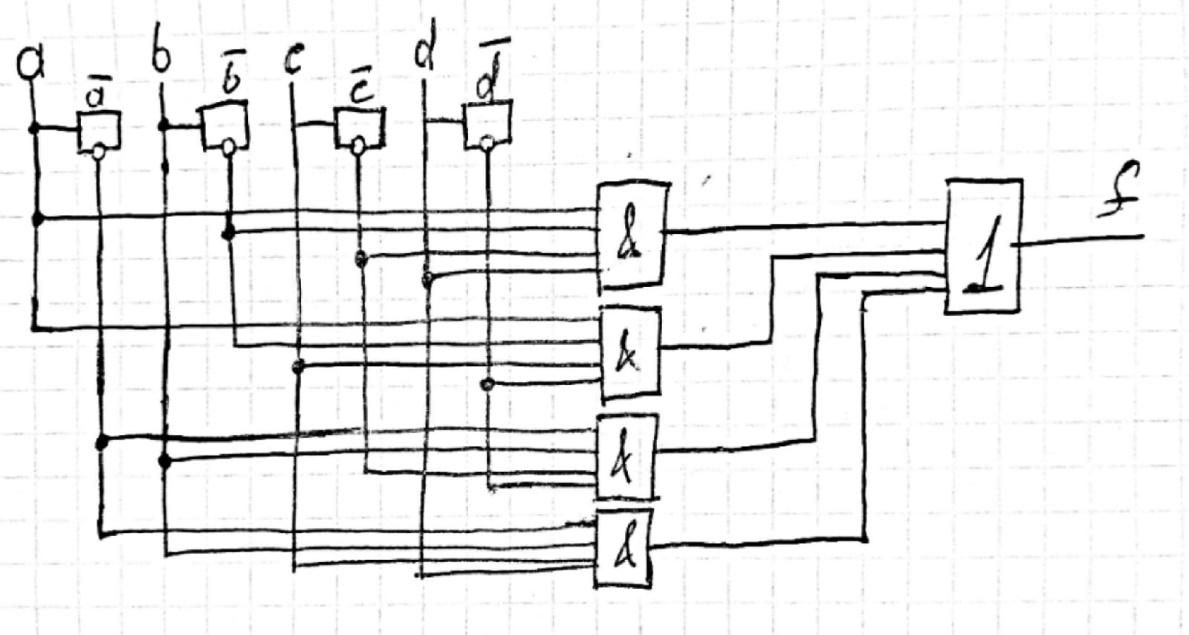
Рисунок 2 - Минимальная логическая схема для первой таблицы представлена
КСМ для второй таблицы
Во второй таблице под кодом bcd плюс стоит под числами 0 и 5, под кодом abd плюс стоит под числом 2.
Полученные минтермы:
Код bcd:
-
0 = 010 =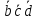 ;
; -
5 = 111 = .
.
Код abd:
-
2 = 010 =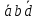 .
.
Каноническая сумма минтермов:
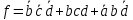
Минимальная логическая схема для второй таблицы представлена на рисунке 3.
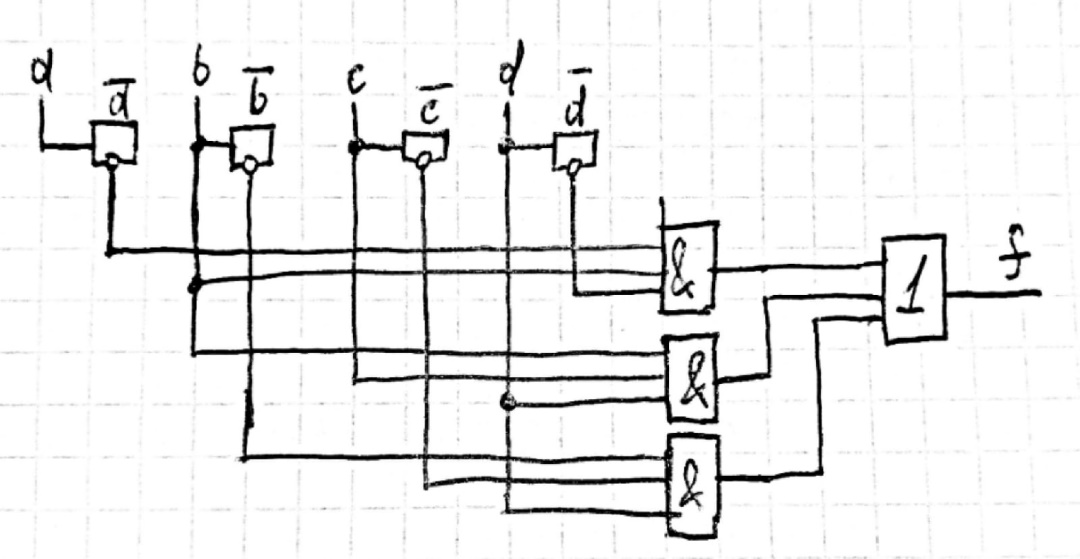
Рисунок 3 - Минимальная логическая схема для второй таблицы
КСМ для третьей таблицы
В третьей таблице под кодом abc плюс стоит под числами 4 и 6, под кодом acd плюс стоит под 6.
Полученная сумма минтермов:
Код abc:
4 = 100 =
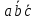
6 = 110 =
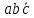 ;
;Код аcd:
6 = 110 =
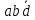
Каноническая сумма минтермов:
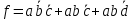
Минимальная логическая схема для третьей таблицы представлена на рисунке 4.
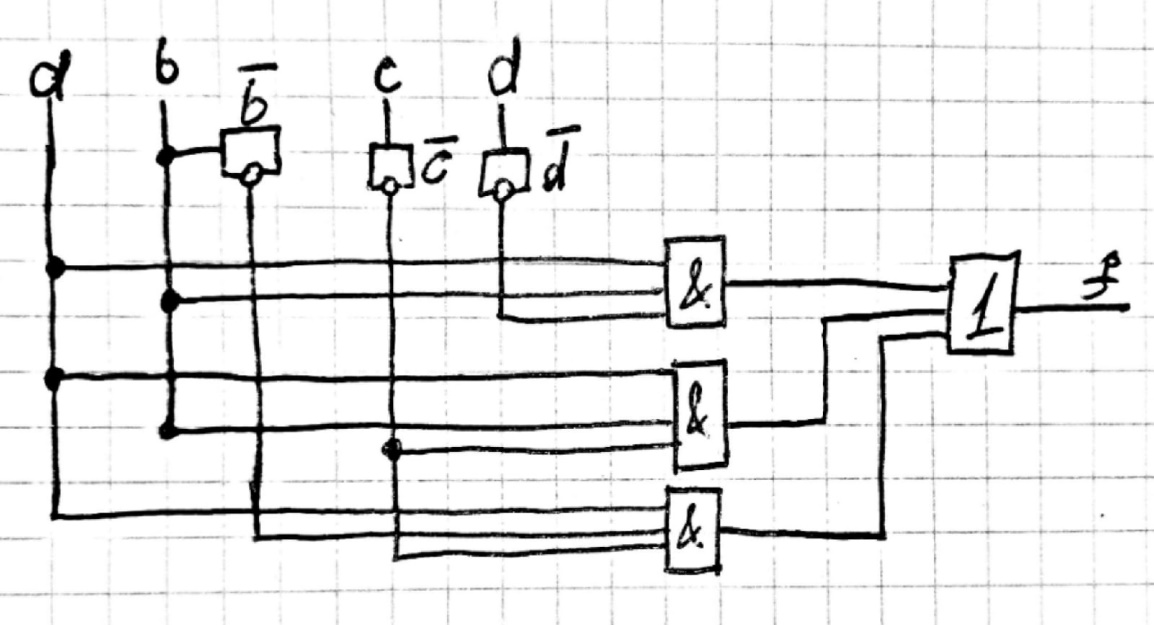
Рисунок 4 - Минимальная логическая схема для третьей таблицы
3 Задание
Минимизировать заданную логическую схему и написать соответствующую каноническую сумму минтермов.
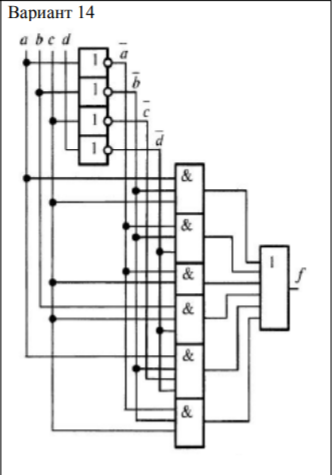
1) Составление логической функции