Файл: Быстрый переход Определение предела последовательности. Подпоследовательность. Частичный предел.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 04.12.2023

Просмотров: 81

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Быстрый переход: Определение предела последовательности. Подпоследовательность. Частичный предел. Критерий Коши. Свойство сходящихся последовательностей. Теорема о пределе промежуточной последовательности. Определение предела функции. Теорема о пределе промежуточной функции. Первый замечательный предел. Бесконечно малые функции. Теорема о связи бесконечно малых и бесконечно больших функций. (+ определение б/б функций limf(x) = ∞) Теорема о пределе произведения бесконечно малой и ограниченной функции Второй замечательный предел. Раскрытие неопределенностей Сравнение бесконечно малых. Эквивалентность бесконечно малых. Основные эквивалентности. Теорема о разности эквивалентных бесконечно малых. Теорема о замене эквивалентности в пределе отношения. Непрерывность функции в точке. Теорема о непрерывности арифметических действий. о непрерывности сложной функции. Непрерывность функции на отрезке. Свойства функций непрерывных на отрезке. Точки разрыва и их классификация Производная, ее геометрический и механический смысл Теорема о связи непрерывности и дифференцируемости Арифметические действия с производными Таблица производных Производные сложной и обратной функции Дифференциал, его связь с производной, геометрический смысл, инвариантность. Теорема Ролля, ее геометрический смысл Теорема Лагранджа, ее геометрический смысл. Теорема Коши. Правило Лопиталя. Многочлен Тейлора, формула Тейлора. Остаточный член формулы Тейлора в формах Пеано и Лагранджа Локальный экстремум функции одного переменного. Необходимое и достаточное условия экстремума. Геометрический смысл второй производной. Точки перегиба. Асимптоты графика функции. Существование наклонной асимптоты. Частные производные функции нескольких переменных. Теорема о равенстве смешанных производных. Дифференцируемость функции нескольких переменных. Дифференциал. Локальный экстремум функции нескольких переменных. Необходимое условие экстремума. Нахождение производных по определению 1Нахождение производных по определению 2<Справка>1. Определение предела последовательности. Подпоследовательность. Частичный предел. Предел числовой последовательности: Число   называется пределом последовательности   , если для любого   существует номер   такой, что для любого    выполняется неравенство   : Подпоследовательность: Пусть задана некоторая последовательность { } и есть строго возрастающая последовательность натуральных чисел. Тогда последовательность называется подпоследовательностью последовательности { }.Будем писать:   и говорить, что последовательность { } стремится к плюс бесконечности, если для каждого числа   найдется номер  , такой что   при любом  Аналогично даются определения для случая  , Частичный предел последовательности: Частичным пределом последовательности называется предел какой-нибудь сходящейся подпоследовательности. Частичным пределом последовательности называется предел какой-либо её подпоследовательности, если существует хотя бы одна подпоследовательность, имеющая предел. В противном случае, говорят, что у последовательности нет частичных пределов. Пример:Пусть  Эта последовательность расходится, но ее подпоследовательности   и   сходятся соответственно к 1 и -1.Таким образом эти числа являются частичными пределами последовательности   <Вернуться назад> 2. Критерий Коши. Свойство сходящихся последовательностей. Теорема о пределе промежуточной последовательности. Свойства фундаментальных последовательностей: Если последовательность   фундаментальная, тогда существует такой номер   , что в  -окрестности точки   содержатся все члены последовательности, начиная с этого номера.Последовательность   сходится тогда и только тогда, когда она ограниченная и верхний предел равен нижнему. <Вернуться назад>3. Определение предела функции. Теорема о пределе промежуточной функции.Первый замечательный предел. Предел: Пределпромежуточной функции Если имеет место соотношение   и  ,  , то и  или говорят: если функция F(х) заключена между двумя функциями s(х) и g(х), стремящимися к одному и тому же пределу, то она также стремится к этому пределу.Пример: Найти предел функции   в точке  , если известно, что имеет место соотношение:   и   ,  Решение: Найдем пределы заданных функций   и   при  : А тогда по теореме о предел промежуточной функции и Ответ.  Первый замечательный предел: Так как при α→0 имеем sinα→0, то говорят, что первый замечательный предел раскрывает неопределённость вида 0/0. Вместо переменной α под знаком синуса и в знаменателе может быть расположено любое выражение, если: Выражения под знаком синуса и в знаменателе одновременно стремятся к нулю, т.е. присутствует неопределенность вида 0/0. Выражения под знаком синуса и в знаменателе совпадают. Часто используются также следствия из первого замечательного предела: <Вернуться назад> 4. Бесконечно малые функции. Теорема о связи бесконечно малых и бесконечно больших функций. Бесконечно малые функции: Функция   называется бесконечно малой функцией (б.м или б/м) при   (или в точке   ), если Пример:Функция   является бесконечно малой (б.м) функцией при  .Основные свойства бесконечно малых функций:1)Сумма конечного числа б.м функций является функцией б.м. 2)Произведение б.м функции на ограниченную есть функция б.м. 3)Произведение двух б.м функций есть функция б.м. 4)Произведение б.м функции на константу является б.м функцией.5)Частное от деления б.м функции на функцию, предел которой не равен 0, есть функция б.м.6)Функция 1/f(x), обратная к б.м функции, есть функция бесконечно большая. Верно и обратное.Теорема:Пусть   - предел функции   в точке  :   . Тогда заданную функцию можно представить в виде  , где   - б.м. функция. Верно и обратное утверждение. Теорема о связи бесконечно малых и бесконечно больших функций: Если функция - функция бесконечно малая ( ), то функция есть бесконечно большая функция и наоборот.Доказательство:Пусть - бесконечно малая функция при , т.е. . Тогда для любого числа существует такое число , что для всех , удовлетворяющих неравенству , выполняется неравенство , т.е. , т.е. , где . А из этого следует, что функция - бесконечно большая.<Вернуться назад> 5. Теорема о пределе произведения бесконечно малой и ограниченной функции. Теорема: Произведение бесконечно малой функции a(x) на ограниченную функцию f(x) при x→a (или при x→∞) есть бесконечно малая функция. Доказательство: Так как функция f(x) ограничена, то существует число М такое, что при всех значениях x из некоторой окрестности точки a|f(x)|≤M. Кроме того, так как a(x) – бесконечно малая функция при x→a, то для произвольного ε>0 найдется окрестность точки a, в которой будет выполняться неравенство |α(x)|< ε/M. Тогда в меньшей из этих окрестностей имеем | αf|< ε/M= ε. А это и значит, что af – бесконечно малая. Для случая x→∞ доказательство проводится аналогично. Из доказанной теоремы вытекают: Следствие 1. Если и , то .Следствие 2. Если и c=const, то .<Вернуться назад> 6. Второй замечательный предел. Раскрытие неопределенностей Второй замечательный предел: Второй замечательный предел служит для раскрытия неопределенности 1∞ и выглядит следующим образом: Обратим внимание на то, что в формуле для второго замечательного предела в показателе степени должно стоять выражение, обратное тому, которое прибавляется к единице в основании (так как в этом случае можно ввести замену переменных и свести искомый предел ко второму замечательному пределу). <Вернуться назад>7. Сравнение бесконечно малых. Эквивалентность бесконечно малых. Основные эквивалентности. Таблица эквивалентных бесконечно малых: П усть - бесконечно малая при .Эквивалентность всех величин таблицы можно доказать, основываясь на равенстве .<Вернуться назад> 8. Теорема о разности эквивалентных бесконечно малых. Теорема о замене эквивалентности в пределе отношения. Теорема: Разность двух эквивалентных бесконечно малых функций есть бесконечно малая более высокого порядка, чем каждая из них. (См. 7. Сравнение бесконечно малых)Справедливо и обратное утверждение: если разность б.м.ф. α и ß есть бесконечно малая высшего порядка, чем α или ß, то α и ß — эквивалентные бесконечно малые.Действительно, так как т. е. Отсюда т. е. αß. Аналогично, если то α ß. Теорема о замене эквивалентности в пределе отношения: Числитель или знаменатель можно заменить на эквивалентные. Доказательство: Пусть в точке х = х0 имеем f(x)

Схема исследования функции на выпуклость, вогнутость

Виды асимптот:

Нахождение наклонной асимптоты

Геометрический смысл дифференциала





Так как при переходе через точку   производная сменила свой знак с "-" на "+", то в этой точке функция достигает минимума (или минимального значения), причем  .

Замечание. Также можно определить интервалы монотонности функции: так как на интервале  производная  , то на этом интервале функция   является убывающей; на интервале   производная  , значит заданная функция возрастает на нем.

Ответ. 

Теорема

(Второе достаточное условие экстремума)

Пусть для функции   выполнены следующие условия:

  1. она непрерывна в окрестности точки  ;

  2. первая производная   в точке  ;

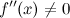  3.  в точке   .

Тогда в точке   достигается экстремум, причем, если  , то в точке   функция  имеет минимум; если  , то в точке   функция   достигает максимум.

<Вернуться назад>
24. Геометрический смысл второй производной. Точки перегиба.
Теорема

(Об условиях выпуклости или вогнутости графика функции)

Пусть функция   определена на интервале   и имеет непрерывную, не равную нулю в точке   вторую производную. Тогда, если   всюду на интервале  , то функция имеет вогнутость на этом интервале, если  , то функция имеет выпуклость.
Определение

Точкой перегиба графика функции   называется точка  , разделяющая промежутки выпуклости и вогнутости.

Теорема

(О необходимом условии существования точки перегиба)

Если функция   имеет перегиб в точке 
, то   или не существует.

Теорема

(О достаточном условии существования точки перегиба)

Если:

  1. первая производная   непрерывна в окрестности точки  ;

  2. вторая производная   или не существует в точке  ;

  3.  при переходе через точку   меняет свой знак,

тогда в точке   функция   имеет перегиб.

Схема исследования функции на выпуклость, вогнутость


  1. Найти вторую производную функции.

  2. Найти точки, в которых вторая производная равна нулю или не существует.

  3. Исследовать знак производной слева и справа от каждой найденной точки и сделать вывод об интервалах выпуклости и точках перегиба.

Пример

Задание. Найти интервалы выпуклости/вогнутости функции 

Решение. Найдем вторую производную заданной функции:



Находим точки, в которых вторая производная равна нулю, для этого решаем уравнение  :



Исследуем знак второй производной слева и справа от полученной точки:



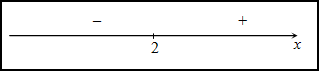
Так как на промежутке   вторая производная  , то на этом промежутке функция  выпукла; в силу того, что на промежутке   вторая производная   - функция вогнута. Так как при переходе через точку   вторая производная сменила знак, то эта точка является точкой перегиба графика функции.

Ответ. Точка   - точка перегиба графика функции.

На промежутке   функция выпукла, на промежутке   функция вогнута.
<Вернуться назад>
25. Асимптоты графика функции. Существование наклонной асимптоты.

Виды асимптот:


Определение

Прямая   называется вертикальной асимптотой графика функции  , если хотя бы одно из предельных значений   или   равно   или   .

Замечание. Прямая   не может быть вертикальной асимптотой, если функция непрерывна в точке   . Поэтому вертикальные асимптоты следует искать в точках разрыва функции.


Определение

Прямая   называется горизонтальной асимптотой графика функции  , если хотя бы одно из предельных значений   или   равно   .

Замечание. График функции может иметь только правую горизонтальную асимптоту или только левую.

Определение

Прямая   называется наклонной асимптотой графика функции  , если

Нахождение наклонной асимптоты


Теорема

(условиях существования наклонной асимптоты)

Если для функции   существуют пределы   и  , то функция имеет наклонную асимптоту   при   .

Замечание

Горизонтальная асимптота является частным случаем наклонной при   .

Замечание

Если при нахождении горизонтальной асимптоты получается, что  , то функция может иметь наклонную асимптоту.

Замечание

Кривая   может пересекать свою асимптоту, причем неоднократно.

Пример

Задание. Найти асимптоты графика функции 

Решение. Область определения функции:



а) вертикальные асимптоты: прямая   - вертикальная асимптота, так как



б) горизонтальные асимптоты: находим предел функции на бесконечности:




то есть, горизонтальных асимптот нет.

в) наклонные асимптоты  :







Таким образом, наклонная асимптота:   .

Ответ. Вертикальная асимптота - прямая   .

Наклонная асимптота - прямая   .

<Вернуться назад>
26. Частные производные функции нескольких переменных. Теорема о равенстве смешанных производных.




Теорема 1(для функции двух переменных)


Пусть функция f(x,y) определенна со своими частными производными fx,fy,fxy,fyx в некоторой окрестности точки (x0,y0), и при этом fxy и  fyx непрерывны в этой точке. Тогда  эти производные равны ( результат не зависит от порядка дифференцирования).

fxy(x0,y0)=fyx(x0,y0)

Теорема 2(обобщение)


Если у функции n переменных смешанные частные производные m-го порядка непрерывны в некоторой точке, а производные низших порядков непрерывны в окрестности этой точки, то частные производные порядка m  не зависят от порядка дифференцирования.
<Вернуться назад>
27. Дифференцируемость функции нескольких переменных. Дифференциал.
Обозначения:
 или   – частная производная по «икс»
 или   – частная производная по «игрек»

Полный дифференциал первого порядка функции двух переменных имеет вид:


И по неоднократным просьбам читателей, полный дифференциал второго порядка:

Пусть функция   дифференцируема в точке  , то есть приращение этой функции можно представить в виде суммы двух слагаемых: линейного относительно   и нелинейного членов:

Смотрите также файлы