Файл: Быстрый переход Определение предела последовательности. Подпоследовательность. Частичный предел.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 04.12.2023

Просмотров: 77

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Быстрый переход: Определение предела последовательности. Подпоследовательность. Частичный предел. Критерий Коши. Свойство сходящихся последовательностей. Теорема о пределе промежуточной последовательности. Определение предела функции. Теорема о пределе промежуточной функции. Первый замечательный предел. Бесконечно малые функции. Теорема о связи бесконечно малых и бесконечно больших функций. (+ определение б/б функций limf(x) = ∞) Теорема о пределе произведения бесконечно малой и ограниченной функции Второй замечательный предел. Раскрытие неопределенностей Сравнение бесконечно малых. Эквивалентность бесконечно малых. Основные эквивалентности. Теорема о разности эквивалентных бесконечно малых. Теорема о замене эквивалентности в пределе отношения. Непрерывность функции в точке. Теорема о непрерывности арифметических действий. о непрерывности сложной функции. Непрерывность функции на отрезке. Свойства функций непрерывных на отрезке. Точки разрыва и их классификация Производная, ее геометрический и механический смысл Теорема о связи непрерывности и дифференцируемости Арифметические действия с производными Таблица производных Производные сложной и обратной функции Дифференциал, его связь с производной, геометрический смысл, инвариантность. Теорема Ролля, ее геометрический смысл Теорема Лагранджа, ее геометрический смысл. Теорема Коши. Правило Лопиталя. Многочлен Тейлора, формула Тейлора. Остаточный член формулы Тейлора в формах Пеано и Лагранджа Локальный экстремум функции одного переменного. Необходимое и достаточное условия экстремума. Геометрический смысл второй производной. Точки перегиба. Асимптоты графика функции. Существование наклонной асимптоты. Частные производные функции нескольких переменных. Теорема о равенстве смешанных производных. Дифференцируемость функции нескольких переменных. Дифференциал. Локальный экстремум функции нескольких переменных. Необходимое условие экстремума. Нахождение производных по определению 1Нахождение производных по определению 2<Справка>1. Определение предела последовательности. Подпоследовательность. Частичный предел. Предел числовой последовательности: Число   называется пределом последовательности   , если для любого   существует номер   такой, что для любого    выполняется неравенство   : Подпоследовательность: Пусть задана некоторая последовательность { } и есть строго возрастающая последовательность натуральных чисел. Тогда последовательность называется подпоследовательностью последовательности { }.Будем писать:   и говорить, что последовательность { } стремится к плюс бесконечности, если для каждого числа   найдется номер  , такой что   при любом  Аналогично даются определения для случая  , Частичный предел последовательности: Частичным пределом последовательности называется предел какой-нибудь сходящейся подпоследовательности. Частичным пределом последовательности называется предел какой-либо её подпоследовательности, если существует хотя бы одна подпоследовательность, имеющая предел. В противном случае, говорят, что у последовательности нет частичных пределов. Пример:Пусть  Эта последовательность расходится, но ее подпоследовательности   и   сходятся соответственно к 1 и -1.Таким образом эти числа являются частичными пределами последовательности   <Вернуться назад> 2. Критерий Коши. Свойство сходящихся последовательностей. Теорема о пределе промежуточной последовательности. Свойства фундаментальных последовательностей: Если последовательность   фундаментальная, тогда существует такой номер   , что в  -окрестности точки   содержатся все члены последовательности, начиная с этого номера.Последовательность   сходится тогда и только тогда, когда она ограниченная и верхний предел равен нижнему. <Вернуться назад>3. Определение предела функции. Теорема о пределе промежуточной функции.Первый замечательный предел. Предел: Пределпромежуточной функции Если имеет место соотношение   и  ,  , то и  или говорят: если функция F(х) заключена между двумя функциями s(х) и g(х), стремящимися к одному и тому же пределу, то она также стремится к этому пределу.Пример: Найти предел функции   в точке  , если известно, что имеет место соотношение:   и   ,  Решение: Найдем пределы заданных функций   и   при  : А тогда по теореме о предел промежуточной функции и Ответ.  Первый замечательный предел: Так как при α→0 имеем sinα→0, то говорят, что первый замечательный предел раскрывает неопределённость вида 0/0. Вместо переменной α под знаком синуса и в знаменателе может быть расположено любое выражение, если: Выражения под знаком синуса и в знаменателе одновременно стремятся к нулю, т.е. присутствует неопределенность вида 0/0. Выражения под знаком синуса и в знаменателе совпадают. Часто используются также следствия из первого замечательного предела: <Вернуться назад> 4. Бесконечно малые функции. Теорема о связи бесконечно малых и бесконечно больших функций. Бесконечно малые функции: Функция   называется бесконечно малой функцией (б.м или б/м) при   (или в точке   ), если Пример:Функция   является бесконечно малой (б.м) функцией при  .Основные свойства бесконечно малых функций:1)Сумма конечного числа б.м функций является функцией б.м. 2)Произведение б.м функции на ограниченную есть функция б.м. 3)Произведение двух б.м функций есть функция б.м. 4)Произведение б.м функции на константу является б.м функцией.5)Частное от деления б.м функции на функцию, предел которой не равен 0, есть функция б.м.6)Функция 1/f(x), обратная к б.м функции, есть функция бесконечно большая. Верно и обратное.Теорема:Пусть   - предел функции   в точке  :   . Тогда заданную функцию можно представить в виде  , где   - б.м. функция. Верно и обратное утверждение. Теорема о связи бесконечно малых и бесконечно больших функций: Если функция - функция бесконечно малая ( ), то функция есть бесконечно большая функция и наоборот.Доказательство:Пусть - бесконечно малая функция при , т.е. . Тогда для любого числа существует такое число , что для всех , удовлетворяющих неравенству , выполняется неравенство , т.е. , т.е. , где . А из этого следует, что функция - бесконечно большая.<Вернуться назад> 5. Теорема о пределе произведения бесконечно малой и ограниченной функции. Теорема: Произведение бесконечно малой функции a(x) на ограниченную функцию f(x) при x→a (или при x→∞) есть бесконечно малая функция. Доказательство: Так как функция f(x) ограничена, то существует число М такое, что при всех значениях x из некоторой окрестности точки a|f(x)|≤M. Кроме того, так как a(x) – бесконечно малая функция при x→a, то для произвольного ε>0 найдется окрестность точки a, в которой будет выполняться неравенство |α(x)|< ε/M. Тогда в меньшей из этих окрестностей имеем | αf|< ε/M= ε. А это и значит, что af – бесконечно малая. Для случая x→∞ доказательство проводится аналогично. Из доказанной теоремы вытекают: Следствие 1. Если и , то .Следствие 2. Если и c=const, то .<Вернуться назад> 6. Второй замечательный предел. Раскрытие неопределенностей Второй замечательный предел: Второй замечательный предел служит для раскрытия неопределенности 1∞ и выглядит следующим образом: Обратим внимание на то, что в формуле для второго замечательного предела в показателе степени должно стоять выражение, обратное тому, которое прибавляется к единице в основании (так как в этом случае можно ввести замену переменных и свести искомый предел ко второму замечательному пределу). <Вернуться назад>7. Сравнение бесконечно малых. Эквивалентность бесконечно малых. Основные эквивалентности. Таблица эквивалентных бесконечно малых: П усть - бесконечно малая при .Эквивалентность всех величин таблицы можно доказать, основываясь на равенстве .<Вернуться назад> 8. Теорема о разности эквивалентных бесконечно малых. Теорема о замене эквивалентности в пределе отношения. Теорема: Разность двух эквивалентных бесконечно малых функций есть бесконечно малая более высокого порядка, чем каждая из них. (См. 7. Сравнение бесконечно малых)Справедливо и обратное утверждение: если разность б.м.ф. α и ß есть бесконечно малая высшего порядка, чем α или ß, то α и ß — эквивалентные бесконечно малые.Действительно, так как т. е. Отсюда т. е. αß. Аналогично, если то α ß. Теорема о замене эквивалентности в пределе отношения: Числитель или знаменатель можно заменить на эквивалентные. Доказательство: Пусть в точке х = х0 имеем f(x)

Схема исследования функции на выпуклость, вогнутость

Виды асимптот:

Нахождение наклонной асимптоты

Геометрический смысл дифференциала





где   при  .

Определение

Дифференциалом функции называется линейная относительно   часть приращения функции. Она обозначается как   или  . Таким образом:



Замечание

Дифференциал функции составляет основную часть ее приращения.

Замечание

Наряду с понятием дифференциала функции вводится понятие дифференциала аргумента. По определению дифференциал аргумента есть приращение аргумента:

Замечание

Формулу для дифференциала функции можно записать в виде:



Отсюда получаем, что



Итак, это означает, что производная может быть представлена как обыкновенная дробь - отношение дифференциалов функции и аргумента.

Геометрический смысл дифференциала


Дифференциал функции в точке   равен приращению ординаты касательной, проведенной к графику функции в этой точке, соответствующему приращению аргумента  .
<Вернуться назад>
28. Локальный экстремум функции нескольких переменных. Необходимое условие экстремума.
Локальный экстремум функции двух переменных 

     Необходимое условие локального экстремума дифференцируемой функции 

     Если   - точка экстремума функции f, то

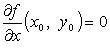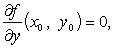 и   или 



     Достаточные условия локального экстремума дважды дифференцируемой функции 

     Обозначим   

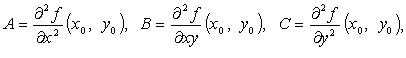
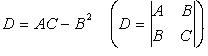
(Также принято обозначать: D-M1,2,3 ; A,B,C – Uxx, Uxy, …)

     Если D > 0, A > 0, то   - точка минимума.

     Если D > 0, A < 0, то   - точка максимума.

     Если D < 0, экстремума в точке   нет.

     Если D = 0, необходимы дополнительные исследования.

Пример от 3х переменных:

Решение 
Найдем стационарные точки заданной функции, то есть точки, в которых выполняется необходимое условие существования экстремума. Для функции трех переменных   стационарные точки (координаты точек) находятся из системы 
Для заданной функции  ,  ,   

и система примет вид 
Решениями системы являются   и 
Получили две стационарные точки   и  .
Для проверки достаточных условий экстремума в стационарной точке необходимо определить знаки определителей  , 
 и 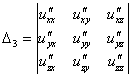  в этой точке.
Найдем  ,  ,  ,  ,  ,  .
Для точки    ,

, 
.

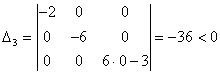Так как  ,  ,  , то в точке   функция имеет максимум, при этом 
.
Для точки    ,

,

.

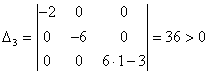Так как  ,  ,  , то в точке   функция не имеет экстремума.
<Вернуться назад>

Справка

1. Q: Как перейти по ссылке на определенный вопрос?

A: Нажать на ссылку, потом - на появившуюся ссылку под ней:


Или “ctrl + ЛКМ”.
2. Q: Как добавить закладку?

A: Выделить фрагмент текста, на который будет сделана закладка, нажать в верхнем меню “Вставка” -> “Закладка”

3. Q: Как добавить ссылку на закладку?

A: Выделить текст будущей ссылки, нажать сочетание “ctrl + K”, кликнуть в появившеся меню “Закладки >” и выбрать нужную закладку.
4. Q: Как вставить разделитель после вопроса, чтобы следующий всегда был на новой странице?

A: Нажать ctrl + Enter

Спасибо!

Всем, кто писал ответы на вопросы:

  1. Линар Саитов

  2. Арсений Автомонов

  3. Хитров Николай



<Вернуться назад>

By IKBO-08-16 & IKBO-13-17

2016-2018
©mirea


Смотрите также файлы