Файл: Управление системами и процессами технической эксплуатации летательных аппаратов.docx
Добавлен: 05.12.2023
Просмотров: 184
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
1.Управление объемами запасных частей для замены отказавших изделий.
2. УПРАВЛЕНИЕ ТЕХНИЧЕСКИМ СОСТОЯНИЕМ ИЗДЕЛИЙ, ПОДВЕРЖЕННЫХ ИЗНОСУ И СТАРЕНИЮ
3. МОДЕЛИ УПРАВЛЯЕМЫХ СОСТОЯНИЙ ПРОЦЕССА ТЕХНИЧЕСКОЙ ЭКСПЛУАТАЦИИ ЛА
3.1 Определение параметров модели управляемого состояния использования по назначению
4.1 Определение параметров закона распределения Вейбулла наработки изделия до отказа
4.2 Оценка параметров функции затрат на техническое обслуживание и ремонт ЛА
4.3 Определение оптимальной периодичности технического обслуживания и ремонта ЛА.
4.4 Управление режимами технического обслуживания и ремонта изделий ЛА.
4.3 Определение оптимальной периодичности технического обслуживания и ремонта ЛА.
Предположив, что время жизни изделия стремится к бесконечности определим время работы ЛА без восстановления (периодичность обслуживания)
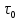 :
: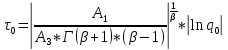
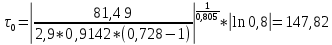
 Проверим условие бесконечного времени жизни ЛА:
Проверим условие бесконечного времени жизни ЛА: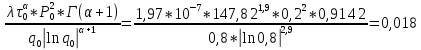
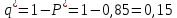
Т.к. условие бесконечного времени жизни изделия выполняется, то периодичность ТОиР τ0=147.82 ч – является оптимальной.
4.4 Управление режимами технического обслуживания и ремонта изделий ЛА.
Рассчитаем оптимальное времени ТОиР (τ0) варьируя параметром полного
восстановления («качества восстановления» P0)
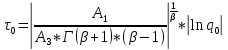
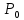 | 0,16 | 0,18 | 0,2 | 0,22 | 0,24 |
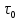 | 115,50 | 131,46 | 147,82 | 164,59 | 181,80 |
Исходя из полученных данных строим график зависимости оптимального времени ТОиР от параметра восстановления (рис.4.1)

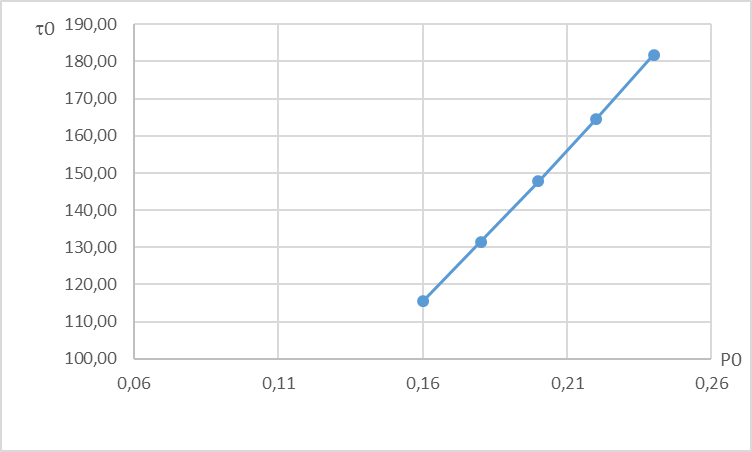
Рис.4.1. Зависимость оптимального времени ТОиР от параметра восстановления
Вывод по задаче №4: Рассчитанные показатели изделия, с учетом затрат на его ТО позволяют оценить время жизни изделия. Чем выше вероятность полного восстановления изделия, тем больше время его жизни в эксплуатационном периоде.
 Общий вывод
Общий вывод
В данной курсовой работе, были выполнены следующие задачи:
-
Определено потребное количество запасных изделий для эксплуатации -
парка ЛА- N=160 запасных частей; -
Определена возможная длительность эксплуатации изделий для парка ЛА с учетом замены отказавших; -
Определили зависимость параметра изделия от наработки для математического ожидания и среднего квадратического отклонения при двух фиксированных значения наработки; -
Определена зависимость параметра изделия от наработки для математического ожидания и среднего квадратического отклонения при трех фиксированных значения наработки; -
Определены параметры модели управляемого состояния использования по назначению; -
Выявлены параметры управляемого состояния ТОиР с детерминированной периодичностью и переменным объемом работ. -
Рассчитаны параметры закона распределения Вейбулла наработки изделия до отказа; -
Произведена оценка параметров функции затрат на техническое обслуживание и ремонт ЛА; -
Определена оптимальная периодичность технического обслуживания и ремонта изделий ЛА;
 ПРИЛОЖЕНИЕ
ПРИЛОЖЕНИЕ
Таблица П.1.1
Значения коэффициента Стьюдента
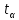
| | | | |||||
| 0.8 | 0.9 | 0.95 | 0.98 | 0.99 | 0.995 | 0.999 | |
| 2 | 1.886 | 2.920 | 4.303 | 6.965 | 9.925 | 14.09 | 31.60 |
| 3 | 1.638 | 2.353 | 3.182 | 4.541 | 5.841 | 7.453 | 12.92 |
| 4 | 1.533 | 2.132 | 2.776 | 3.747 | 4.604 | 5.595 | 8.610 |
| 5 | 1.476 | 2.015 | 2.571 | 3.365 | 4.032 | 4.773 | 6.869 |
| 6 | 1.440 | 1.943 | 2.447 | 3.143 | 3.707 | 4.317 | 5.959 |
| 7 | 1.415 | 1.895 | 2.365 | 2.998 | 3.500 | 4.029 | 5.408 |
| 8 | 1.397 | 1.860 | 2.306 | 2.897 | 3.355 | 3.833 | 5.041 |
| 9 | 1.383 | 1.833 | 2.262 | 2.821 | 3.250 | 3.690 | 4.781 |
| 10 | 1.372 | 1.813 | 2.228 | 2.764 | 3.169 | 3.581 | 4.587 |
| 11 | 1.363 | 1.796 | 2.201 | 2.718 | 3.106 | 3.497 | 4.437 |
| 12 | 1.356 | 1.782 | 2.179 | 2.681 | 3.055 | 3.428 | 4.318 |
| 13 | 1.350 | 1.771 | 2.160 | 2.650 | 3.012 | 3.373 | 4.221 |
| 14 | 1.345 | 1.761 | 2.145 | 2.625 | 2.977 | 3.326 | 4.141 |
| 15 | 1.341 | 1.753 | 2.131 | 2.603 | 2.947 | 3.286 | 4.073 |
| 16 | 1.337 | 1.746 | 2.120 | 2.584 | 2.921 | 3.252 | 4.015 |
| 17 | 1.333 | 1.740 | 2.110 | 2.567 | 2.898 | 3.222 | 3.965 |
| 18 | 1.330 | 1.734 | 2.101 | 2.552 | 2.878 | 3.197 | 3.922 |
| 19 | 1.328 | 1.729 | 2.093 | 2.540 | 2.861 | 3.174 | 3.883 |
| 20 | 1.325 | 1.725 | 2.086 | 2.528 | 2.845 | 3.153 | 3.850 |
| 22 | 1.321 | 1.717 | 2.074 | 2.508 | 2.819 | 3.119 | 3.792 |
| 24 | 1.318 | 1.711 | 2.064 | 2.492 | 2.797 | 3.091 | 3.745 |
| 26 | 1.315 | 1.706 | 2.056 | 2.479 | 2.779 | 3.067 | 3.707 |
| 28 | 1.313 | 1.701 | 2.048 | 2.467 | 2.763 | 3.047 | 3.674 |
| 30 | 1.310 | 1.697 | 2.042 | 2.457 | 2.750 | 3.030 | 3.646 |
| 40 | 1.303 | 1.684 | 2.021 | 2.423 | 2.705 | 2.971 | 3.551 |
| 50 | 1.299 | 1.676 | 2.009 | 2.403 | 2.678 | 2.936 | 3.496 |
| 60 | 1.296 | 1.671 | 2.000 | 2.390 | 2.660 | 2.915 | 3.460 |
| 80 | 1.292 | 1.664 | 1.990 | 2.374 | 2.639 | 2.887 | 3.416 |
| 100 | 1.290 | 1.660 | 1.984 | 2.364 | 2.626 | 2.871 | 3.391 |
| 150 | 1.287 | 1.655 | 1.976 | 2.352 | 2.609 | 2.849 | 3.357 |
| 200 | 1.286 | 1.653 | 1.972 | 2.345 | 2.601 | 2.839 | 3.340 |
| 300 | 1.284 | 1.650 | 1.968 | 2.339 | 2.592 | 2.828 | 3.323 |
| 500 | 1.283 | 1.648 | 1.965 | 2.334 | 2.586 | 2.82 | 3.310 |
 | 1.282 | 1.645 | 1.960 | 2.326 | 2.576 | 2.807 | 3.291 |
Таблица П.1.2
 Значения
Значения 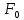 (x)
(x)| X | | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 0 | 0 | 5000 | 5040 | 5080 | 5120 | 5160 | 5199 | 5239 | 5279 | 5319 |
| 0.1 | 0 | 5398 | 5438 | 5478 | 5517 | 5557 | 5596 | 5636 | 5675 | 5714 |
| 0.2 | 0 | 5793 | 5832 | 5871 | 5910 | 5948 | 5987 | 6026 | 6064 | 6103 |
| 0.3 | 0 | 6179 | 6217 | 6255 | 6293 | 6331 | 6368 | 6406 | 6443 | 6480 |
| 0.4 | 0 | 6554 | 6591 | 6628 | 6664 | 6700 | 6736 | 6772 | 6808 | 6844 |
| 0.5 | 0 | 6915 | 6950 | 6985 | 7019 | 7054 | 7088 | 7123 | 7157 | 7190 |
| 0.6 | 0 | 7257 | 7291 | 7324 | 7357 | 7389 | 7422 | 7454 | 7486 | 7517 |
| 0.7 | 0 | 7580 | 7611 | 7642 | 7673 | 7704 | 7344 | 7764 | 7794 | 7823 |
| 0.8 | 0 | 7881 | 7910 | 7939 | 7967 | 7995 | 8023 | 8051 | 8078 | 8106 |
| 0.9 | 0 | 8159 | 8186 | 8212 | 8238 | 8264 | 8289 | 8315 | 8340 | 8365 |
| 1 | 0 | 8413 | 8438 | 8461 | 8485 | 8508 | 8531 | 8554 | 8577 | 8599 |
| 1.1 | 0 | 8643 | 8665 | 8686 | 8708 | 8729 | 8749 | 8770 | 8790 | 8810 |
| 1.2 | 0 | 8849 | 8869 | 8888 | 8907 | 8925 | 8944 | 8962 | 8980 | 8997 |
| 1.3 | 0.9 | 0320 | 0490 | 0658 | 0824 | 0988 | 1149 | 1308 | 1466 | 1621 |
| 1.4 | 0.9 | 1924 | 2073 | 2220 | 2364 | 2507 | 2647 | 2785 | 2922 | 3056 |
| 1.5 | 0.9 | 3319 | 3448 | 3574 | 3699 | 3822 | 3943 | 4062 | 4179 | 4295 |
| 1.6 | 0.9 | 4520 | 4630 | 4738 | 4845 | 4950 | 5053 | 5154 | 5254 | 5352 |
| 1.7 | 0.9 | 5543 | 5637 | 5728 | 5818 | 5907 | 5994 | 6080 | 6164 | 6246 |
| 1.8 | 0.9 | 6407 | 6485 | 6562 | 6637 | 6712 | 6784 | 6856 | 6926 | 6995 |
| 1.9 | 0.9 | 7128 | 7193 | 7257 | 7320 | 7381 | 7441 | 7500 | 7558 | 7615 |
| 2 | 0.9 | 7725 | 7778 | 7831 | 7882 | 7932 | 7982 | 8030 | 8077 | 8124 |
| 2.1 | 0.9 | 8214 | 8257 | 8300 | 8341 | 8382 | 8422 | 8461 | 8500 | 8537 |
| 2.2 | 0.9 | 8610 | 8645 | 8679 | 8713 | 8745 | 8778 | 8809 | 8840 | 8870 |
| 2.3 | 0.9 | 8928 | 8956 | 8983 | 9010 | 9036 | 9061 | 9086 | 9111 | 9134 |
| 2.4 | 0.99 | 1802 | 2024 | 2240 | 2451 | 2656 | 2857 | 3053 | 3244 | 3431 |
| 2.5 | 0.99 | 3790 | 3963 | 4132 | 4297 | 4457 | 4614 | 4766 | 4915 | 5060 |
| 2.6 | 0.99 | 5339 | 5473 | 5603 | 5731 | 5855 | 5975 | 6093 | 6207 | 6319 |
| 2.7 | 0.99 | 6533 | 6636 | 6736 | 6833 | 6928 | 7020 | 7110 | 7197 | 7282 |
| 2.8 | 0.99 | 7445 | 7523 | 7599 | 7673 | 7744 | 7814 | 7882 | 7948 | 8012 |
| 2.9 | 0.99 | 8134 | 8193 | 8250 | 8305 | 8359 | 8411 | 8462 | 8511 | 8559 |
| 3 | 0.99 | 8650 | 8694 | 8736 | 8777 | 8817 | 8856 | 8893 | 8930 | 8965 |
 Таблица П.1.2 (продолжение)
Таблица П.1.2 (продолжение)Значения
 (x)
(x)| X | | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3.0 | 0.99 | 8650 | 8694 | 8736 | 8777 | 8817 | 8856 | 8893 | 8965 | 8999 |
| 3.1 | 0.93 | 0324 | 0646 | 0957 | 1260 | 1553 | 1836 | 2112 | 2636 | 2886 |
| 3.2 | 0.93 | 3129 | 3363 | 3590 | 3810 | 4024 | 4230 | 4429 | 4810 | 4991 |
| 3.3 | 0.93 | 5166 | 5335 | 5499 | 5658 | 5811 | 5959 | 6103 | 6376 | 6505 |
| 3.4 | 0.93 | 6631 | 6752 | 6869 | 6982 | 7091 | 7197 | 7299 | 7493 | 7585 |
| 3.5 | 0.93 | 7674 | 7760 | 7842 | 7922 | 7999 | 8074 | 8146 | 8282 | 8347 |
| 3.6 | 0.93 | 8409 | 8469 | 8527 | 8583 | 8637 | 8689 | 8739 | 8834 | 8879 |
| 3.7 | 0.93 | 8922 | 8964 | 9004 | 9043 | 9080 | 9116 | 9150 | 9216 | 9247 |
| 3.8 | 0.94 | 2765 | 3052 | 3327 | 3593 | 3848 | 4094 | 4331 | 4777 | 4988 |
| 3.9 | 0.94 | 5190 | 5385 | 5573 | 5753 | 5926 | 6092 | 6252 | 6554 | 6696 |
| 4.0 | 0.94 | 6833 | 6964 | 7090 | 7211 | 7327 | 7439 | 7546 | 7748 | 7843 |
| 4.1 | 0.94 | 7934 | 8022 | 8106 | 8186 | 8264 | 8338 | 8409 | 8542 | 8605 |
| 4.2 | 0.94 | 8665 | 8723 | 8778 | 8832 | 8882 | 8931 | 8978 | 9066 | 9107 |
| 4.3 | 0.95 | 1460 | 1837 | 2198 | 2544 | 2876 | 3193 | 3497 | 4066 | 4332 |
| 4.4 | 0.95 | 4588 | 4832 | 5065 | 5288 | 5502 | 5706 | 5902 | 6268 | 6439 |
| 4.5 | 0.95 | 6602 | 6759 | 6908 | 7051 | 7187 | 7318 | 7442 | 7675 | 7784 |
| 4.6 | 0.95 | 7888 | 7987 | 8081 | 8172 | 8258 | 8340 | 8419 | 8566 | 8634 |
| 4.7 | 0.95 | 8699 | 8761 | 8821 | 8877 | 8931 | 8983 | 9032 | 9124 | 9166 |
| 4.8 | 0.96 | 2067 | 2554 | 2822 | 3173 | 3508 | 3827 | 4131 | 4696 | 4958 |
| 4.9 | 0.96 | 5208 | 5446 | 5673 | 5888 | 6094 | 6289 | 6475 | 6821 | 6981 |
| 5.0 | 0.96 | 7134 | 7278 | 7416 | 7548 | 7672 | 7791 | 7904 | 8113 | 8210 |
| 5.1 | 0.96 | 8302 | 8389 | 8472 | 8551 | 8626 | 8698 | 8765 | 8891 | 8949 |
| 5.2 | 0.97 | 004 | 056 | 105 | 152 | 197 | 240 | 280 | 354 | 388 |
| 5.3 | 0.97 | 421 | 452 | 481 | 509 | 539 | 560 | 584 | 628 | 648 |
| 5.4 | 0.97 | 667 | 685 | 702 | 718 | 734 | 748 | 762 | 787 | 799 |
| 5.5 | 0.97 | 810 | 821 | 831 | 840 | 849 | 857 | 865 | 880 | 886 |
| 5.6 | 0.97 | 893 | 899 | 905 | 910 | 915 | 920 | 924 | 933 | 936 |
| 5.7 | 0.98 | 40 | 44 | 47 | 50 | 53 | 55 | 58 | 63 | 65 |
| 5.8 | 0.98 | 67 | 69 | 71 | 72 | 74 | 75 | 77 | 79 | 81 |
| 5.9 | 0.98 | 82 | 83 | 84 | 85 | 86 | 87 | 87 | 89 | 90 |
| 6.0 | 0.98 | 90 | - | - | - | - | - | - | - | - |
Таблица П.1.3
 Коэффициенты для распределения Вейбулла
Коэффициенты для распределения Вейбулла| | | | |
| 0.2 | 120 | 1900 | 15.83 |
| 0.3 | 8.86 | 46.9 | 5.29 |
| 0.4 | 3.32 | 10.4 | 3.14 |
| 0.5 | 2 | 4.47 | 2.24 |
| 0.6 | 1.50 | 2.61 | 1.74 |
| 0.7 | 1.27 | 1.86 | 1.46 |
| 0.8 | 1.13 | 1.43 | 1.26 |
| 0.9 | 1.05 | 1.17 | 1.11 |
| 1 | 1.00 | 1.00 | 1.00 |
| 1.1 | 0.965 | 0.878 | 0.910 |
| 1.2 | 0.941 | 0.787 | 0.837 |
| 1.3 | 0.924 | 0.716 | 0.775 |
| 1.4 | 0.911 | 0.659 | 0.723 |
| 1.5 | 0.903 | 0.612 | 0.678 |
| 1.6 | 0.897 | 0.574 | 0.640 |
| 1.7 | 0.892 | 0.540 | 0.605 |
| 1.8 | 0.889 | 0.512 | 0.575 |
| 1.9 | 0.887 | 0.485 | 0.547 |
| 2 | 0.886 | 0.463 | 0.523 |
| 2.1 | 0.886 | 0.441 | 0.489 |
| 2.2 | 0.886 | 0.425 | 0.480 |
| 2.3 | 0.886 | 0.409 | 0.461 |
| 2.4 | 0.887 | 0.394 | 0.444 |
| 2.5 | 0.887 | 0.380 | 0.428 |
| 3 | 0.893 | 0.326 | 0.365 |
| 3.5 | 0.900 | 0.285 | 0.316 |
| 4 | 0.906 | 0.255 | 0.281 |