Файл: Курсовая работа по дисциплине Теория вероятностей и математическая статистика.docx
Добавлен: 05.12.2023
Просмотров: 264
Скачиваний: 15
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
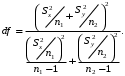
В данном случае t-статистику, используем для проверки нулевой гипотезы о равенстве средних величин при различных неизвестных дисперсиях, называют критерием Фишера-Беренса.
| сред.N | 67,73487 | 72,22808 |
| сред.D | 228,1546 | 224,3688 |
| наблюдение | 100 | 100 |
| | | |
| S^2 | 114,0773 |
| S | 14,69199228 |
| t одинаковые дисперсии | -1,529343091 |
| bf | 198 |
| t(разные дисперсии) | -1,486081773 |
| bf | 99,0065579 |
Рисунок 14. Расчет данных
Используем «Двухвыборочный t-тест с различными дисперсиями» Анализ данных MS Exсel.
| Двухвыборочный t-тест с различными дисперсиями | | |
| | | |
| | Переменная 1 | Переменная 2 |
| Среднее | 67,73486772 | 72,22808031 |
| Дисперсия | 230,4591532 | 226,6351319 |
| Наблюдения | 100 | 100 |
| Гипотетическая разность средних | 0 | |
| df | 198 | 198 |
| t-статистика | -2,101619412 | -2,101619412 |
| P(T<=t) одностороннее | 0,018425712 | 0,018425712 |
| t критическое одностороннее | 1,652585784 | 1,652585784 |
| P(T<=t) двухстороннее | 0,036851425 | 0,036851425 |
| t критическое двухстороннее | 1,972017478 | 1,972017478 |
Рисунок 15. Двухвыборочный t-тест с различными дисперсиями
В данном случае t-статистику, используемую для проверки нулевой гипотезы о равенстве средних величин при различных неизвестных дисперсиях, называют критерием Фишера-Беренса.
Вывод: t расч. < t критич. Следовательно, гипотеза о равенстве средних значений при неизвестной дисперсии подтверждается.
Список литературы
1. Гмурман, В.Е. Теория вероятностей и математическая статистика: учеб. пособие для вузов / В.Е. Гмурман. – 10-е изд., стер. – М.: Высш. шк., 2004. – 479 с.
2. Ветров, А.Н. Статистические программные системы: учебное
пособие ⁄ А.Н. Ветров, А.Л. Борисов, Ю.Г. Козлова. – Тверь: Тверской
государственный технический университет, 2014. – 152 с.
3. Ветров, А.Н. Методические указания и задания к курсовой работе по дисциплине Теория вероятностей и статистика / А.Н. Ветров. – Тверь: ТвГТУ, 2017. – 25 с.
5. Дисперсионный двухфакторный анализ [Электронный ресурс] // refdb.ru: сайт. – Режим доступа: https://refdb.ru/look/1210036.html
5. Шеффе, Г. Дисперсионный анализ / Г. Шеффе. – М.: Наука, 1980. 512 с.