Файл: Курсовая работа по дисциплине Теория вероятностей и математическая статистика.docx
Добавлен: 05.12.2023
Просмотров: 258
Скачиваний: 15
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство науки и высшего образования Российской Федерации
Тверской государственный технический университет
Кафедра информационных систем
КУРСОВАЯ РАБОТА
по дисциплине «Теория вероятностей и математическая статистика»
Студент 2 курса ФИТ факультета
Б.ИСТ.РВС.21.35 группы заочного отделения
Калашников М.С
Проверил: к.т.н. Ветров А.Н.
Тверь
2022
ОГЛАВЛЕНИЕ
1.РАСЧЕТ ОСНОВНЫХ ПОКАЗАТЕЛЕЙ СТАТИСТИКИ 4
2. Построение гистограммы 8
3. Проверка соответствия закона распределения наблюдаемым данным 9
4. Проверка гипотезы о равенстве средних величин при известной дисперсии 11
5. Проверка гипотезы о равенстве дисперсий 12
6. Проверка гипотезы о равенстве средних величин при неизвестной дисперсии 13
Список литературы 16
Введение
Курсовая работа выполнена в системе EXCEL с использованием статистических функций и пакета анализа.
Данная работа состоит из 9 разделов:
-
Расчет основных показателей статистики. -
Построение гистограммы. -
Проверка соответствия закона распределения наблюдаемым данным. -
Проверка гипотезы о равенстве средних величин при известной дисперсии. -
Проверка гипотезы о равенстве средних величин при неизвестной дисперсии. -
Проверка гипотезы о равенстве дисперсий. -
Однофакторный дисперсионный анализ. -
Двухфакторный дисперсионный анализ без повторений и с повторениями. -
Простая линейная регрессия.
Работа выполнялась в табличном процессоре MS Excel с использованием статистических функций и пакета анализа.
Статистическая информация для выполнения заданий генерируется самостоятельно с помощью инструмента анализа «Генерация» пакета EXCEL в соответствии с вариантом задания.
В соответствии с вариантом задания установлены следующие значения:
1. Математическое ожидание mx = 70;
2. Стандартное отклонение σx = 14.
-
РАСЧЕТ ОСНОВНЫХ ПОКАЗАТЕЛЕЙ СТАТИСТИКИ
Показатели описательной статистики делятся на несколько групп.
1. Показатели положения описывают положение данных на числовой оси. Примеры таких показателей: средняя арифметическая,
средняя гармоническая, медиана и другие характеристики.
2. Показатели разброса описывают степень разброса данных относительно своего центра. К этой группе относятся: дисперсия, стандартное отклонение, размах выборки, эксцесс и т.п. Эти показатели определяют, насколько кучно основная масса данных группируется около центра.
3. Показатели асимметрии характеризуют симметрию распределения данных около своего центра. К ним можно относятся коэффициент асимметрии, положение медианы относительно среднего и т.п.
4. Показатели, описывающие закон распределения, дают представление о законе распределения данных. К ним относятся таблицы частот, средняя арифметическая, медиана, дисперсия, стандартное отклонение, гистограмма.
Задание:
1. Сгенерировать 100 значений нормально распределенной случайной величины с параметрами mx, σx
2. Рассчитать значения показателей описательной статистики.
3. Рассчитанные значения свести в таблицу вида
Ход работы:
1. Генерируем 100 значений нормально распределенной случайной величины с параметрами mx, σx
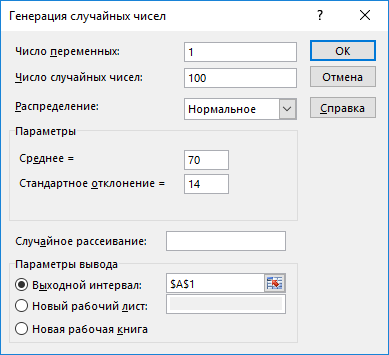
Рисунок 1. Генерация случайных чисел
Рассчитаем значения показателей описательной статистики
1. Среднее.
Функция СРЗНАЧ рассчитывает значение средней арифметической величины по формуле
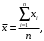
где xi – i-ое значение выборки, n – число наблюдаемых значений выборки.
2. Медианой называется значение признака, приходящееся на середину упорядоченной совокупности. Используется функция МЕДИАНА.
3. Модой называется чаще всего встречающаяся варианта или то значение признака, которое соответствует максимальной точке теоретической кривой распределения. Используется функция МОДА.
4. Выборочная дисперсия рассчитывается по выборочным данным. Для
этого используется выражение, где
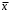 – среднее арифметическое выборки.
– среднее арифметическое выборки.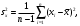
Используется функция ДИСП.
5. Выборочное стандартное отклонение оценивает разброс возможных значений случайной величины вокруг её среднего. Формула для расчета стандартного отклонения
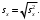
Для определения в Excel использовалась функция СТАНДОТКЛОН.
6. Стандартная (средняя) ошибка повторной собственно-случайной выборки определяется по формуле
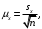
где sx – выборочная дисперсия, n – число наблюдаемых значений выборки.
7. Эксцесс характеризует так называемую «крутость», т.е. островершинность или плосковершинность кривой распределения.
Для определения в Excel используется функция ЭКСЦЕСС, которая рассчитывает значение эксцесса как для симметричных, так и для асимметричных распределений.
8. Симметричным является распределение, в котором частоты любых двух вариант, равноотстоящих в обе стороны от центра распределения, равны между собой. Для симметричных распределений средняя арифметическая, мода и медиана равны между собой. С учетом этого показатель асимметрии основан на соотношении показателей центра распределения: чем больше разница между х, Mo, Me, тем больше асимметрия ряда. При этом если Mo < Me, асимметрия правосторонняя, если Mo > Me – асимметрия левосторонняя.
Функция СКОС определяет величину асимметрии по выборочной совокупности. При этом если As > О – асимметрия правосторонняя (положительная), если As < О — асимметрия левосторонняя
9. Функции МИН и МАКС используются для определения минимального и максимального значений признака в выборке.
10. Интервалрассчитываются как разность между наибольшим (хmах) и наименьшим (хmin) значениями выборки, т.е. и называется размах вариации.
R = xmax– xmin
11. Функция СЧЕТ используется для определения величины
n.
12. Функции НАИБОЛЬШИЙ и НАИМЕНЬШИЙ определяют k-ое максимальное и минимальное значения в выборке.
13. Уровень надёжности. Предельная ошибка выборки связана со средней ошибкой выборки соотношением
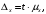
где t – коэффициент доверия, который определяется в зависимости от того, с какой доверительной вероятностью нужно гарантировать результаты выборочного обследования.
В Excel коэффициент доверия t рассчитывался через функцию СТЬЮДРАСПОБР, в которой в качестве аргументов задаются уровень значимости и число степеней свободы df.
Число степеней свободы df зависит от объема выборки n и связано с ним выражением df = n – 1.
Границы доверительного интервала для математического ожидания находятся из выражения
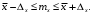
-
Рассчитанные значения вставляем в таблицу. -
| 67,92443027 | средние значение | 1 |
| 67,88264176 | медиана | 2 |
| #Н/Д | мода | 3 |
| 218,0349869 | дисперсия | 4 |
| 14,69199228 | отклонение | 5 |
| 1,469199228 | ошибка(дисп/кор n) | 6 |
| 0,16673091 | эксцес | 7 |
| 0,246254297 | ассеметрия | 8 |
| 36,07413777 | минимум | 9 |
| 113,9133146 | максимум | 10 |
| 77,83917681 | интервал(макс/мин) | 11 |
| 100 | величина n | 12 |
| 74,04219463 | наибольшее | 13 |
| 0,062865953 | уровень надежности | 14 |
Рисунок 2. Расчет показателей описательной статистики