Файл: Курсовая работа по дисциплине Теория вероятностей и математическая статистика.docx

Рисунок 10. Двухвыборочный Z-тест для средних

Вывод: z расч. < z крит., следовательно, гипотеза о равенстве средних значений при известной дисперсии принимается.

---

5. Проверка гипотезы о равенстве дисперсий

Задание:

Используя данные задания 4 проверить гипотезу о равенстве дисперсий

Ход работы:

В математической статистике доказывается, что если гипотеза о равенстве дисперсий двух случайных величин выполняется: H₀: 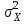= 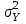, то величина 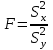распределена в соответствии с законом распределения Фишера.

Это отношение F называют дисперсионным отношением Фишера и используют в качестве критерия проверки нулевой гипотезы.

Распределение Фишера характеризуется наличием степеней свободы, которые вычисляются по формулам:



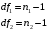
Поскольку величина F – неотрицательная, то критическая область данной величины будет принадлежать интервалу (0;+¥).

Альтернативными являются гипотезы:

Н₁: 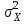> 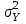при >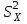

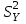
Н₂: 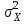< 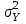при <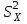

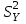
_{Используем «}Двух выборочный F-тест для дисперсии» Анализ данных MS Exсel.

Двухвыборочный F-тест для дисперсии
	Переменная 1	Переменная 2
Среднее	67,73486772	72,22808031
Дисперсия	230,4591532	226,6351319
Наблюдения	100	100
df	99	99
F	1,01687303	1,01687303
P(F<=f) одностороннее	0,466913235	0,466913235
F критическое одностороннее	1,394061257	1,394061257

---

Рисунок 11. Двух выборочный F-тест для дисперсии

Вывод: Удвоенное значение р (уровень для одностороннего критерия P(F<=f)) будет больше, чем уровень значимости (0,05), следовательно, нулевая гипотеза о равенстве дисперсий не отклоняется.

6. Проверка гипотезы о равенстве средних величин при неизвестной дисперсии

Задание:

Требуется для вашего варианта проверить гипотезу H₀: m_x=m_y, предположив, что соответствующие генеральные совокупности имеют нормальное распределение

1. 
   с одинаковыми дисперсиями;
   
2. 
   с различными дисперсиями.
   

Ход работы:

Для проверки гипотезы о равенстве средних (математических ожиданий) двух независимых нормальных распределений с неизвестными дисперсиями и используется t-тест

Относительно дисперсий и можно выдвинуть следующие два предположения:

1) Обе дисперсии неизвестны, но предполагается, что они равны между собой, т.е. = .

2) Обе дисперсии неизвестны и предполагается, что они не равны между собой, т.е. ≠ .

В случае, когда обе дисперсии неизвестны, но предполагается, что они равны между собой, мы имеем дело с двумя оценками и одной и той же дисперсии = .

То в этом случае строится объединённая оценка:

---

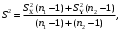
Где S² – это объединённая оценка дисперсии = = .

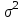В математической статистике доказывается, что если нулевая гипотеза о равенстве математических ожиданий H₀: m_x=m_yвыполняется, то величина tвычисляется по формуле:



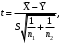
Где 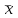и 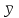– средние арифметические величины, n₁ – число наблюдений в первой выборке, n₂ – число наблюдений во второй выборке, S – выборочное стандартное отклонение.

Статистика tимеет распределение Стьюдента. Число степеней свободы определяется по формуле:



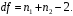
Эту t-статистику и используем в качестве критерия при проверке нулевой гипотезы о равенстве математических ожиданий. Схема проверки аналогична проверке при использовании Z-теста.

сред.N		67,73487			72,22808
сред.D		228,1546			224,3688
наблюдение		100			100
S^2	114,0773
S	14,69199228
t одинаковые дисперсии	-1,529343091
bf	198
t(разные дисперсии)	-1,486081773
bf	99,0065579

---

Рисунок 12. Расчет данных

Используем «Двухвыборочный t-тест с одинаковыми дисперсиями» Анализ данных MS Exсel.

Двухвыборочный t-тест с одинаковыми дисперсиями
	Переменная 1	Переменная 2
Среднее	67,73486772	72,22808031
Дисперсия	230,4591532	226,6351319
Наблюдения	100	100
Объединенная дисперсия	228,5471425
Гипотетическая разность средних	0
df	198	198
t-статистика	-2,101619412	-2,101619412
P(T<=t) одностороннее	0,018425712	0,018425712
t критическое одностороннее	1,652585784	1,652585784
P(T<=t) двухстороннее	0,036851425	0,036851425
t критическое двухстороннее	1,972017478	1,972017478

Рисунок 13. Двухвыборочный t-тест с одинаковыми дисперсиями

В случае, когда дисперсии неизвестны и предполагается, что они равны, используем аналог Z-теста с заменой дисперсий их оценками.

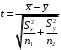- это распределение близко к распределению Стьюдента.

Число степеней свободы вычисляем по следующей формуле:

---