Файл: Курсовая работа по дисциплине Теория вероятностей и математическая статистика.docx

2. Построение гистограммы

Задание:

1. 
   Сгенерировать 100 значений нормально распределенной случайной величины с параметрами m_x, σ_x
   
2. 
   Построить гистограмму
   
3. 
   Построить нормированную эмпирическую функцию распределения
   

Ход работы:

1. 
   Берем из 1 задания 100 значений нормально распределенной случайной величины с параметрами m_x, σ_x.
   
2. 
   Строим гистограмму частот и гистограмму относительны частот.
   

построение гистограмма
№	границы интеграла		частоты	накопленные частоты
1	36,07414	45,93	5	5
2	45,92624	55,39	17	23
3	55,39053	65,15	21	44
4	65,15124	75,30	25	69
5	75,29594	85,08	22	91
6	85,07540	98,48	6	97
7	98,47872	113,91	3	99

Рисунок 3. Расчет показателей

интервал	частоты	относительные частоты
36,07-45,93	5	5%
45,93-55,39	17	23%
55,39-65,15	21	44%
65,15-75,30	25	69%
75,30-85,08	22	91%
85,08-98,48	6	97%
98,48-113,91	3	99%

---

Рисунок 4. Частоты и относительные частоты



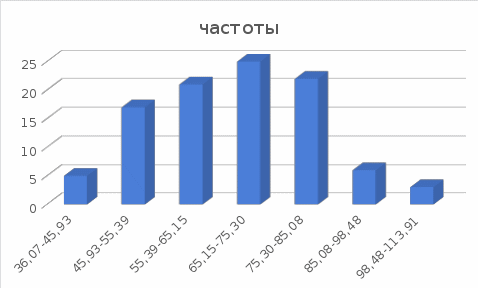
Рисунок 5. Гистограмма частот



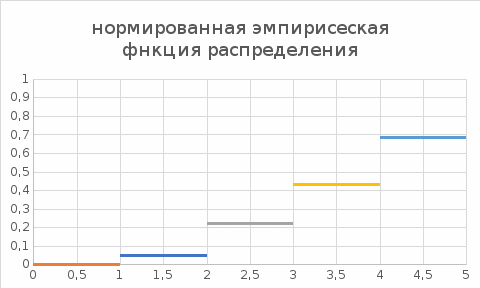
Рисунок 6. Нормированная эмпирическая функция распределения

3. 1   2   3   4   5

---

Проверка соответствия закона распределения наблюдаемым данным

Ход работы:

1. Определяем число значений признака, попадающих в j – ый интервал 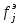и среднее значение признака 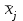для каждого интервала.

2. Вычисляем среднее значение вариационного ряда x.

3. Вычисляем выборочную дисперсию 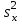и стандартное отклонение 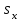вариационного ряда.

4. Вычисляем значения функции плотности нормального распределения для каждого интервала по формуле p_j = НОРМРАСП(), в качестве x используем среднее значение на интервале, параметр ИНТЕГРАЛЬНАЯ = 0.

5. Рассчитываем теоретические частоты нормального распределения по формуле

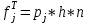где h – длина интервала, n – общее число наблюдаемых значений признака.

6. Рассчитываем значение критерия c² по формуле

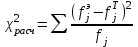
j	границы интервала		эмпирическая частота	середина интервала	p(j)x….0	теоретическая частота	x**2
1	36,07414	45,92624	5	41,00019	0,002768613	1,938028765		0,093756678
2	45,92624	55,39053	17	50,65838	0,00955042	6,685294		1,063931599
3	55,39053	65,15124	21	60,27088	0,020612839	14,42898744		0,431782061
4	65,15124	75,29594	25	70,22359	0,028098162	19,66871358		0,284226149
5	75,29594	85,07540	22	80,18567	0,023332674	16,33287176		0,321163425
6	85,07540	98,47872	6	91,77706	0,010065227	7,045658925		0,010934026
7	98,47872	113,91331	3	106,19602	0,001663142	1,164199685		0,033701628
						Храс		2,239495566
						Хкри		9,487729037

---

Рисунок 7. Проверка соответствия закона распределения

Вывод: Так как 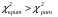, то гипотеза о нормальности распределения СВ принимается.

---

4. Проверка гипотезы о равенстве средних величин при известной дисперсии

Задание:

1. Сгенерировать 2 нормально распределенные переменные. Первая переменная генерируется в соответствии с Вашим вариантом. При генерации второй переменной математическое ожидание увеличивается на 2, а стандартное отклонение в 1,5 раза.

2. Проверить гипотезу о равенстве средних величин

Ход работы 1:

1. 
   Вычисляем статистику Z.
   

сред.X	67,73487
сред.Y	72,22808
дисп.X	228,1546
дисп.Y	224,3688
N.x	100
N.y	100

Рисунок 8. Статистика Z

2. 
   Задаёмся уровнем значимости .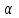
   

Z	-2,11221
a	0,05

Рисунок 9. Уровень значимости

3. 
   Определяем критические точки.
   

Сравниваем рассчитанное в пункте 1 значение Zсо значением критических точек

Двухвыборочный z-тест для средних
	Переменная 1	Переменная 2
Среднее	67,73486772	72,22808031
Известная дисперсия	228,1546	224,3688
Наблюдения	100	100
Гипотетическая разность средних	0
z	-2,112206847
P(Z<=z) одностороннее	0,017334356
z критическое одностороннее	1,644853627
P(Z<=z) двухстороннее	0,034668711
z критическое двухстороннее	1,959963985

---