Файл: Курсовая работа Расчёт сборных железобетонных конструкций многоэтажного производственного здания Студент гр. 181 Сильченко М. К.docx

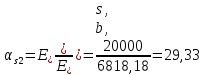
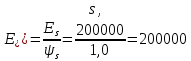МПа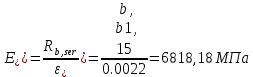



где: значение относительных деформаций бетона при продолжительном действии нагрузки, ε_b1,red=0,0022 (при относительной влажности воздуха 40-75%) принимается по таблице 5.6 [4].



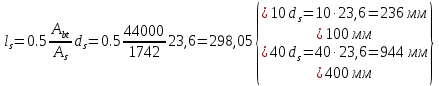
где: A_bt - площадь сечения растянутого бетона.



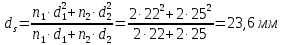
Высота растянутой зоны бетона 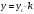; y должна быть не менее 2aи не более 0, 5h.





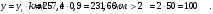
к - поправочный коэффициент, равный: для прямоугольных и тавровых сечений с полкой в сжатой зоне - 0,9;

Так как y=231,66 мм > 0,5h= 0,5∙400=200мм. Принимаем y = 200мм.

A_bt = 220∙200 = 44000 мм².

a_crc,2 - ширина раскрытия трещин от непродолжительного действия всей нагрузки.




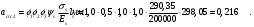
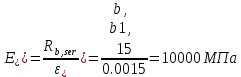
где: значение относительных деформаций бетона при непродолжительном действии нагрузки, ε_b1,red = 0,0015 по п. 5.1.19 [4]








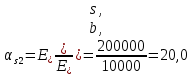
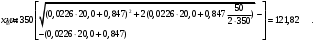
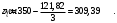
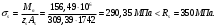
Определение a_crc,3 - ширины раскрытия трещин от непродолжительного действия постоянной и временной длительной нагрузки.



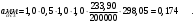
Из расчёта a_crc2: x_m=121,82мм, z_s=309,39 мм;



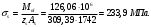
Непродолжительная ширина раскрытия трещин составит:

---

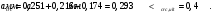
1.3.3 Расчёт плиты по прогибам

Полная кривизна для участков с трещинами в растянутой зоне определяется по формуле 7.3.8 [4]:

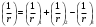, а полный прогиб плиты: 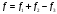где: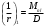

- кривизна от продолжительного действия постоянной и длительной нагрузки

Из расчёта a_crc1: E_bred =E_b1= 6818,18 МПа, α_s1 = 29,33, x_m = 147,24 мм.





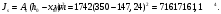
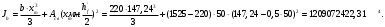
Момент инерции приведённого сечения без учёта растянутого бетона:





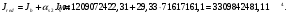
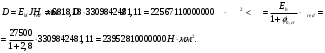
где: 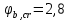- коэффициент ползучести бетона для бетона В20.

Принято:





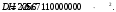
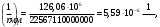
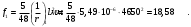
Кривизна от непродолжительного действия всей нагрузки:

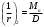, где М_n =156,49 кН∙м

Из расчёта a_crc2: E_bred =E_b1= 10000 МПа, α_s2 = 20,0, x_m = 121,82 мм.













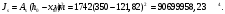
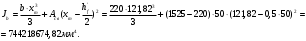
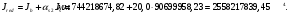
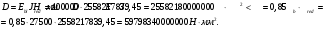
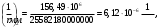
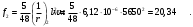
Кривизна от непродолжительного действия постоянной и длительной нагрузки:

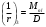, где M_nl = 126,06 кН∙м

Из расчёта a_crc2, (так как нагрузка носит непродолжительный характер): E_bred =E_b1= 10000 МПа, α_s

---

₂ = 20,0, x_m = 121,82 мм,

.







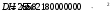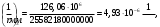
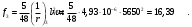
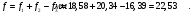
Плита удовлетворяет требованиям таблицы 19 [2]:

а) эстетико-психологическим



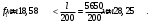
б) конструктивным



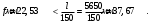
Вывод: плита удовлетворяет требованиям по второй группе предельных состояний.

2. Расчёт сборного ригеля поперечной рамы

Для сборного железобетонного перекрытия, план и разрез которого представлены на рис. 1, требуется рассчитать сборный ригель, используя данные и результаты расчёта плиты. Сетка колонн ll_к = 6,1 х6,2 м. Для ригеля среднего пролета необходимо построить эпюры моментов от нагрузки и его несущей способности.

Армирование ригеля представлено на рисунке 8: ригель с двумя продольными каркасами и двух рядным расположение стержней.



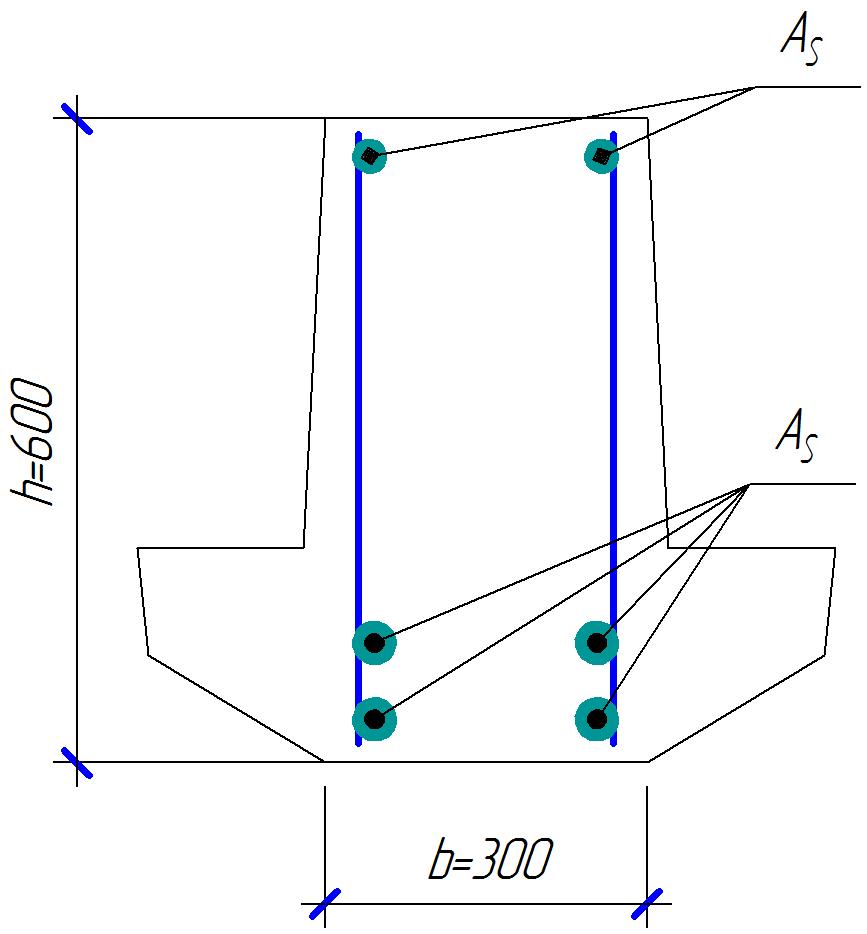
Рисунок 8 – Поперечное сечение ригеля

2.1 Вариант ригеля с двумя каркасами

Данные для расчёта: бетон тяжелый, класс бетона B15, коэффициент работы бетона γ_b1 = 1,0. Расчётные сопротивления бетона с учетом γ_b1 = 1,0 равны: R_b = 1,0∙8,5 = 8,5 МПа; R_bt = 1,0∙0,75 = 0,75 МПа. Продольная и поперечная арматура – класса A500. Коэффициент снижения временной нагрузки к₁ = 0,9.

2.1.1 Расчётные нагрузки

Нагрузка на ригель собирается с грузовой полосы (представленной на рисунке 1) шириной l_к = 6,2 м, равной расстоянию между осями ригелей (по l_к/2 с каждой стороны от оси ригеля).

а) постоянная нагрузка (с γ_n = 1,0 и γ_ƒ = 1,1):

• 
  вес железобетонных плит с заливкой швов g_n = 3,0кН/м² принят по данным типовой серии ИИ 24-1 данных плит:
  

1,0∙1,1∙3,0∙6,2 = 20,46 кН/м;

• 
  вес пола и перегородок:
  

1,0∙1,1∙2,5∙6,2 = 17,05 кН/м;

собственный вес ригеля с приведённой шириной b = 0,4м и высотой h = 0,6 м (размеры предварительные)

1,0∙1,1∙0,4∙0,6∙25 = 6,6 кН/м;

Итого постоянная нагрузка g = 44,11 кН/м.

б) Временная нагрузка с коэффициентом снижения

---

к₁ = 0,9, γ_n = 1,0 и γ_ƒ = 1,2:

p = 1,0∙0,9∙1,2∙20∙6,2 = 133,92 кН/м.

Полная расчетная нагрузка: q = g + p= 44,11+ 133,92 = 178,03 кН/пм.

2.1.2 Расчётные пролёты ригеля

При поперечном сечении колонн 400400 мм (h_c = 400 мм) и вылете консолей l_c = 350 мм расчётные пролёты ригеля равны (см. рис. 9):

• 
  крайний пролет l₁ = l – 1,5h_c - 2l_c = 6,1 – 1,5*0,4 – 2 ∙ 0,35 = 4,8 м.
  
• 
  средний пролет l₂ = l - h_c - 2l_c = 6,1 – 0,4 – 2 ∙ 0,35 = 5,0 м.
  

2.1.3 Расчетные изгибающие моменты

В крайнем пролёте:



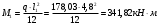
На крайней опоре:



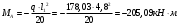
В средних пролетах и на средних опорах:



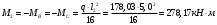
Отрицательные моменты в пролетах при p/g = 133,92/ 44,11= 3,04:

в крайнем пролёте для точки «4» при β = -0,025

M₄=β (g+p) l­₁² = -0,025∙178,03∙4,8 ² = - 102,55 кН∙м.

в среднем пролёте для точки «6» при β = -0,028

M₆=β (g+p) l₂² = -0,028∙178,03∙5,0 ² = - 124,62 кН∙м.

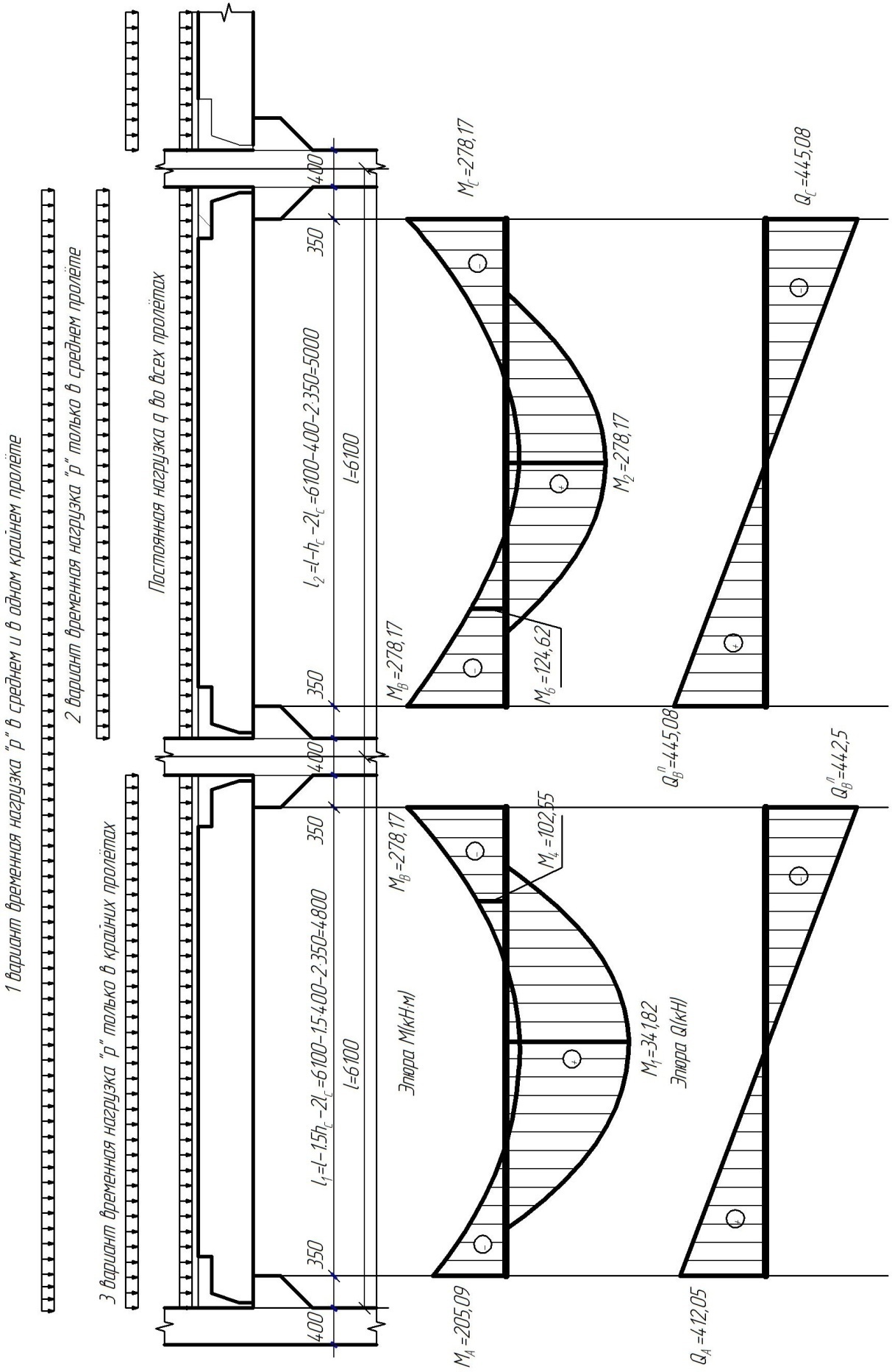Рисунок 9 - К расчёту многопролётного ригеля

2.1.4 Расчетные поперечные силы

Поперечная сила в каждом пролёте определяется как для простой балки с опорными моментами на концах.

На крайней опоре:

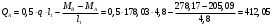кН

На опоре B слева:

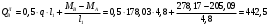кН
На опоре B справа и на средних опорах:

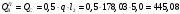кН

2.1.5 Расчет ригеля на прочность по нормальным сечениям

Для арматуры класса A500 ξ_R = 0,493 . Ширина сечения ригеля b = 300мм. Высота ригеля определяется по моменту в крайнем пролёте 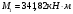, задаваясь значением ξ = 0,35 < ξ_R = 0,493. Откуда α_m = ξ (1 – 0,5ξ) = 0,35(1 – 0,5∙0,35) = 0,289. Сечение рассчитывается как прямоугольное по формуле:

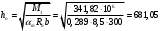мм

h

---

= h₀+a = 585,5 + 70 = 751,05 мм;

принимаем h = 600 мм (h_пл+ 200мм), что соответствует предварительно принятой величине. Пересчёт нагрузки и усилий не требуется.

Расчёт арматуры

Расчётное сопротивление арматуры класса A500 R_s = 435 МПа

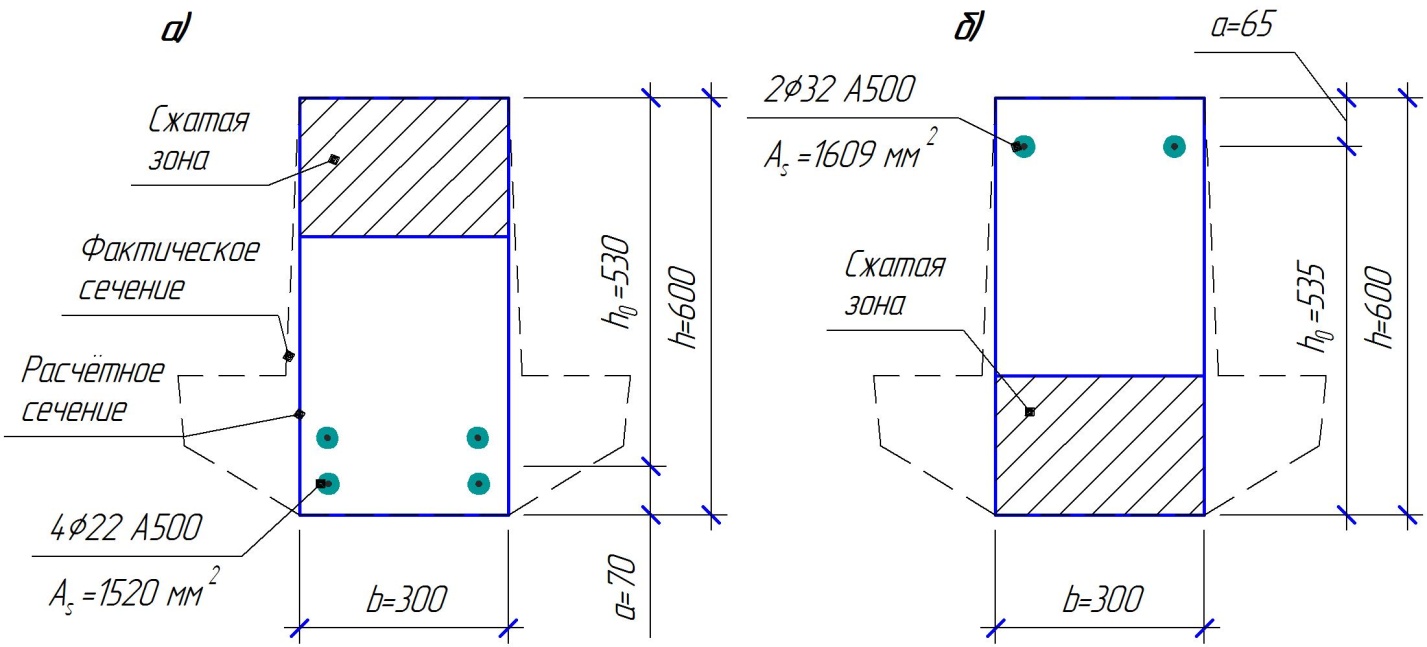
а) Крайний пролёт. M₁ = 341,82 кН∙м; b = 300 мм; h= 600 мм; а=70 мм (предварительно), тогда h₀ = h - a = 600 – 70 = 530 мм. Расчётное сечение представлено на рисунке 10.

;

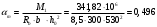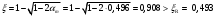, т.к. ξ> ξ_R и разрушение произойдет по сжатой зоне бетона, что недопустимо! Принимаем бетон класса В20. R_b = 1,0∙11,5 = 11,5 МПа; R_bt = 1,0∙0,9 = 0,9 МПа.

;





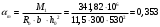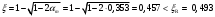
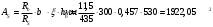
Принято 4Ø25A500 с А_S = 1963 мм² (+2,1%).

a = 30+27/2+60/2 = 73,5 мм (где 30мм - толщина закладной детали, к которой привариваются продольные стержни; 60мм - расстояние между стержнями диаметром 25 мм принимается по приложению К; 27 мм диаметр арматуры 25 по рифам принимается по приложению И), пересчёт а не требуется.
б) Крайняя опора. M_A= -205,09кН∙м;b = 300 мм; h = 600 мм; а=65 мм (предварительно), тогда h₀ = h - a = 600 – 65 = 535 мм (арматура расположена в один ряд по высоте).

;

;



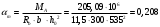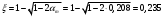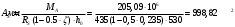
принято 228 A500 с A_s = 1232 мм² (+18,9%). В этом случае h₀ = h - a = 600 – (80 – d/2) = 600 – (80 – 30/2) = 535 мм (где 80мм - расстояние от верха ригеля до низа арматурного стержня), что соответствует предварительно принятому.

в) Верхняя пролетная арматура крайнего пролета по моменту в сечении «4»

M₄ = -102,55 кН∙м; h₀ = h - a = 600 - 65 = 535 мм (однорядная арматура).

;

;

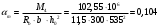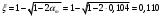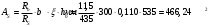принято 218 A400 с A_s= 509 мм² (+8,4 %),

---