ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 14
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ФЕДЕРАЛЬНОЕ Государственное АВТОНОМНОЕ образовательное учреждение Высшего образования
«БЕЛГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ НАЦИОНАЛЬНЫЙ
ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ»
(НИУ «БелГУ»)
ИНСТИТУТ НАУК О ЗЕМЛЕ
Кафедра прикладной геологии и горного дела
Доклад на тему:
"Плоская система сил"
студента очной формы обучения
специальность 21.05.02 Прикладная геология
2 курса группы 08002105
| | Проверил: Проф. Пелипенко Николай Андреевич |
| | |
Дёминой Ксении Дмитриевны
БЕЛГОРОД 2023
Содержание
ВВЕДЕНИЕ 3
1. Теорема о приведении системы сил 4
2. Уравнение равновесия 5
ВВЕДЕНИЕ
Плоская система сил – система сил, расположенных в одной плоскости. Система сил приводится к одной силе – главному вектору и к паре сил, момент которой равен главному моменту. Момент пары сил направлен перпендикулярно к плоскости, в которой лежат силы. В плоских системах нет необходимости использовать векторное представление момента. Теорема Вариньона – если плоская система сил приводится к равнодействующей, то ее момент относительно какой-либо точки равен алгебраической (т.е. с учетом знака) сумме моментов всех сил относит. той же точки.
1. Теорема о приведении системы сил
Любая система сил, действующих на абсолютно твердое тело, может быть заменена одной силой R, равной главному вектору этой системы сил и приложенной к произвольно выбранному центру О, и одной парой сил с моментом LO, равным главному моменту системы сил относительно центра О.
Такая эквивалентная замена данной системы сил силой R и парой сил с моментом LO называют приведением системы сил к центу О.
Рассмотрим здесь частный случай приведения плоской системы сил к центру О, лежащему в той же плоскости (Рисунок 1). В этом случае система сил заменяется одной силой и одной парой сил, лежащих в плоскости действия сил системы. Момент этой пары сил можно рассматривать как алгебраическую величину L
O и изображать на рисунках дуговой стрелкой (алгебраический главный момент плоской системы сил).
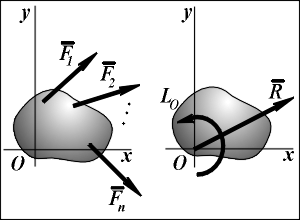
Рисунок 1 – Приведение системы сил к полюсу
В результате приведения плоской системы сил к центру возможны следующие случаи:
-
Если R = 0, LO = 0, то заданная система является равновесной; -
Если хотя бы одна из величин R или LO не равна нулю, то система сил не находится в равновесии. При этом: -
Eсли R = 0 и LO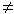 0, то система сил приводится к одной паре сил с моментом LO, причем в этом случае величина момента LO не зависит от выбора центра О.
0, то система сил приводится к одной паре сил с моментом LO, причем в этом случае величина момента LO не зависит от выбора центра О. -
Eсли R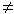 0, то при любом значении LO система сил приводится к равнодействующей силе.
0, то при любом значении LO система сил приводится к равнодействующей силе.
2. Уравнение равновесия
Для равновесия твердрго тела, находящегося под действием плоской системы сил,необходимо и достаточно, чтобы главный вектор этой системы сил и ее алгебраический главный момент были равны нулю, то есть R = 0, LO = 0, где О - любой центр, расположенный в плоскости действия сил системы.
Вытекающие отсюда аналитические условия равновесия (уравнения равновесия) плоской системы сил можно сформулировать в следующих трех формах:
-
Основная форма уравнений равновесия:
для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую из координатных осей и сумма их алгебраических моментов относительно любого центра, лежащего в плоскости действия сил, были равны нулю:
-
Вторая форма уравнений равновесия:
для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы алгебраических моментов всех сил относительно двух центров А и В и сумма их проекций на ось Ox, не перпендикулярную оси Ox, были равны нулю:
-
Третья форма уравнений равновесия (уравнения трех моментов):
для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы алгебраических моментов всех сил относительно любых трех центров А, В и С, не лежащих на одной прямой, были равны нулю:
Уравнения равновесия в форме (I) считаются основными, так как при их использовании нет никаких ограничений на выбор координатных осей и центра моментов.