ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.01.2024
Просмотров: 42
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Тема 1. Работа с матрицами
План
Операции над матрицами 2
Свойства операций над матрицами 3
Работа с матрицами в Excel 4
Матрицей размерности
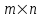 называется таблица чисел, расположенных в
называется таблица чисел, расположенных в 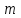 строках и
строках и 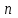 столбцах:
столбцах: 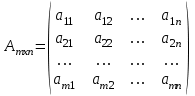 ,
, Матрицы обозначаются латинскими буквами А, В, С, …
Числа, составляющие матрицу, называются ее элементами.
Каждый элемент
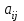 матрицы А имеет два индекса
матрицы А имеет два индекса 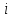 - номер строки,
- номер строки, 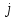 - номер столбца, на пересечении которых стоит элемент
- номер столбца, на пересечении которых стоит элемент 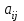 .
. Для матриц используют обозначение
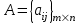 или
или 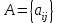 ,
, 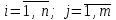 .
. Пример 1. Матрицы
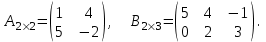
Матрица-строка:
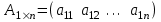 .
.Матрица-столбец:
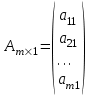 .
.Матрица, у которой число строк равно числу столбцов (
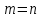 ), называется квадратной, иначе матрица называется прямоугольной.
), называется квадратной, иначе матрица называется прямоугольной. Элементы квадратной матрицы
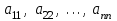 , для которых
, для которых 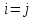 , называются диагональными, а диагональ матрицы, на которой они находятся, - главной диагональю.
, называются диагональными, а диагональ матрицы, на которой они находятся, - главной диагональю. Единичной матрицей называется квадратная матрица, у которой элементы, стоящие на главной диагонали, равны
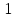 , а остальные элементы равны
, а остальные элементы равны 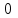 :
: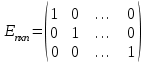 .
.Квадратная матрица, у которой все элементы, кроме диагональных, равны 0, называется диагональной:
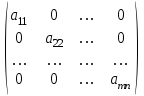 .
.Операции над матрицами
1. Равенство матриц.
Матрица
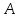 называется равной матрице
называется равной матрице 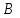 , если они одинаковой размерности и их соответствующие элементы равны.
, если они одинаковой размерности и их соответствующие элементы равны.2. Транспонирование матриц.
Если элементы каждой строки матрицы
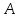 строки записать в том же порядке в столбцы матрицы
строки записать в том же порядке в столбцы матрицы 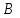 , то матрица
, то матрица 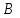 называется транспонированной матрицей. Она обозначается
называется транспонированной матрицей. Она обозначается 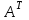 .
. 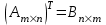 .
.Пример 2. Дана матрица
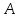 . Получить матрицу
. Получить матрицу 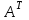 .
.Решение.
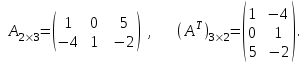
3. Сложение (вычитание) матриц.
Суммой (разностью) матриц
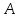 и
и 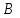 одинаковой размерности называется матрица
одинаковой размерности называется матрица 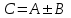 , которая имеет ту же размерность, каждый элемент
, которая имеет ту же размерность, каждый элемент 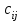 которой равен сумме (разности) соответствующих элементов матриц
которой равен сумме (разности) соответствующих элементов матриц 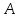 и
и 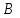 :
: 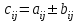 .
.4. Умножение матрицы на число.
Произведением матрицы
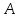 любой размерности на произвольное число
любой размерности на произвольное число 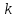 называется матрица
называется матрица 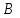
той же размерности, у которой каждый элемент
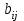 равен произведению элементов
равен произведению элементов  на число
на число  :
: 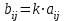 .
. Пример 3. Дана матрица
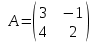 . Найти
. Найти 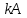 , если
, если 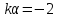 .
. Решение.
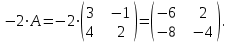
Матрица
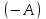 называется противоположной для матрицы
называется противоположной для матрицы  .
.5. Умножение матриц.
Произведением матрицы
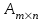 на матрицу
на матрицу 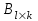 называется матрица
называется матрица 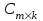 , удовлетворяющая следующим условиям:
, удовлетворяющая следующим условиям:-
матрица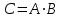 существует, если число столбцов первой матрицы
существует, если число столбцов первой матрицы  равно числу строк второй матрицы
равно числу строк второй матрицы  ;
; -
число строк матрицы
матрицы 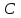 равно числу строк
равно числу строк  матрицы
матрицы  , а число столбцов
, а число столбцов  матрицы
матрицы 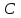 равно числу столбцов
равно числу столбцов  матрицы
матрицы  ;
; -
каждый элемент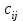 матрицы
матрицы 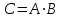 равен сумме произведений элементов
равен сумме произведений элементов  -ой строки матрицы
-ой строки матрицы  на элементы
на элементы  -ого столбца матрицы
-ого столбца матрицы  :
:
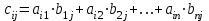 .
.Пример 4. Даны матрицы
 и
и  . Найти произведение
. Найти произведение 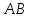 .
.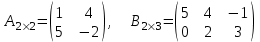
Решение.
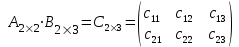

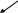
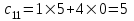
№ строки
 № столбца
№ столбца 
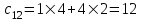 , и так далее.
, и так далее.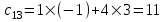 ,
, 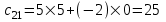 ,
,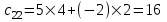 ,
,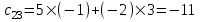 .
.Итак, матрица
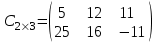 .
.Операции деления для матриц нет.
6. Возведение матрицы в степень.
 -ой степенью матрицы
-ой степенью матрицы  называется такая матрица, которая получена умножением матрицы саму на себя
называется такая матрица, которая получена умножением матрицы саму на себя  раз:
раз: 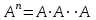 .
. Свойства операций над матрицами
Свойства операции транспонирования матриц.
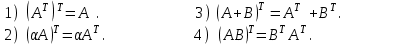
Свойства операции сложения матриц
-
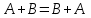 - коммутативность.
- коммутативность.
-
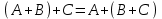 - ассоциативность.
- ассоциативность.
-
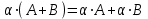 – дистрибутивность относительно сложения матриц.
– дистрибутивность относительно сложения матриц.
-
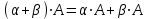 – дистрибутивность относительно сложения чисел.
– дистрибутивность относительно сложения чисел.
Свойства умножения матрицы на число
-
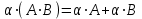 ;
;
-
 ;
;
-
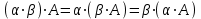 ;
;
-
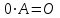 .
.
Свойства операции умножения матриц
-
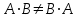 - матрицы не перестановочны относительно умножения, даже если определены оба произведения
- матрицы не перестановочны относительно умножения, даже если определены оба произведения  и
и 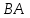 . Перестановочными могут быть только квадратные матрицы одного и того же порядка.
. Перестановочными могут быть только квадратные матрицы одного и того же порядка. -
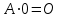 ,
,
-
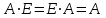 ,
,
-
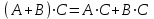 дистрибутивность.
дистрибутивность.
-
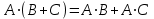 дистрибутивность.
дистрибутивность.
-
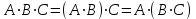 ассоциативность.
ассоциативность. -
Если определено произведение , то определено и произведение
, то определено и произведение 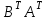 и выполняется равенство
и выполняется равенство 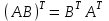 , где индексом
, где индексом 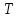 обозначается транспонированная матрица.
обозначается транспонированная матрица.
Работа с матрицами в Excel
В Excel матрицы рассматриваются как массивы.
Массивы можно использовать для создания формул, которые возвращают некоторое множество результатов или оперируют на множестве значений, а не на отдельных значениях, а не на отдельных значениях.
Массивы могут быть одномерные или двумерные. Нельзя использовать объемный массив с использованием нескольких листов книги.
Формула массива действует на нескольких множествах значений, называемых массивами аргументов, и возвращает одно или несколько значений.
Диапазон массива