ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.01.2024
Просмотров: 40
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
- это блок ячеек, который имеет общую формулу массива.
Правила для формул массива:
Если действия выполнены правильно, EXCEL заключает формулу в фигурные скобки, указывая тем самым, что она является формулой массива. Не вводить фигурные скобки самим, т.к. EXCEL расценит это как ввод текстового значения.
Если удерживать нажатой только клавишу SHIFT, формула будет введена как обычная формула в активную ячейку.
Если удерживать нажатой только клавишу CTRL, формула будет введена как обычная формула во все выделенные ячейки.
Для изменения или чистки массива выделить весь массив и активизировать строку формул, при этом фигурные скобки вокруг формулы исчезнут. Изменить или очистить формулу, затем нажать CTRL+SHIFT+ENTER.
Чтобы выделить весь массив, щелкнуть по любой ячейке в массиве и нажать CTRL + /
Чтобы переместить содержимое диапазона массива, выделить весь массив, CTRL +X, затем выделить новый диапазон, CTRL +C, или перетащить выделенный диапазон в новое место.
Можно:
Пример 1. Сложить матрицы А1:С3 и Е1:G3
Аналогично выполняется вычитание матриц.
Пример 2. Умножение матрицы А1:С3 на коэффициент 1,5
Функции работы с матрицами
Категория Математические
МУМНОЖ(массив1,массив2,…) - умножение матриц
МОБР(массив) - нахождение обратной матрицы
МОПРЕД(массив) - вычисление определителя матрицы
Категория Ссылки и массивы
ИНДЕКС(массив) - извлечение из матрицы элемента по номеру строки и столбца
ЧСТРОК(массив), ЧИСЛСТОЛБ(массив) - определение числа строк и столбцов
ТРАНСП(массив) - транспонирование матрицы
Этапы выполнения умножения матриц с помощью МУМНОЖ:
В віделенной области появится результат произведения 2 матриц.
ТРАНСП - вместо матриц можно обрабатывать таблицы, включая заголовки. При выделении области для результата необходимо помнить, что число строк должно быть равно числу столбцов исходной матрицы, а число столбцов - числу строк исходной матрицы.
Решение системы линейных уравнений
Общий вид системы уравнений:
a11x1+a12x2+….+a1nxn=b1
………………………………
am1x1+am2x2+…amnxn=bm
Обозначим:
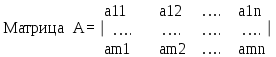
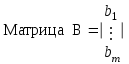
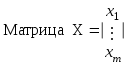
тогда можно записать систему уравнений в матричной форме:
А*Х=В,
для нахождения матрицы Х:
А-1*А*Х=А-1*В
т.е.
Х=А-1*В,
где А-1 - матрица, обратная матрице А.
Порядок решения системы уравнений:
Пример.
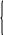
2х1 + 3х2 + 4х3 = 5
3х1 + 4х2 - х3 = 3
4х1 + 5х2 - 2х3 = 3
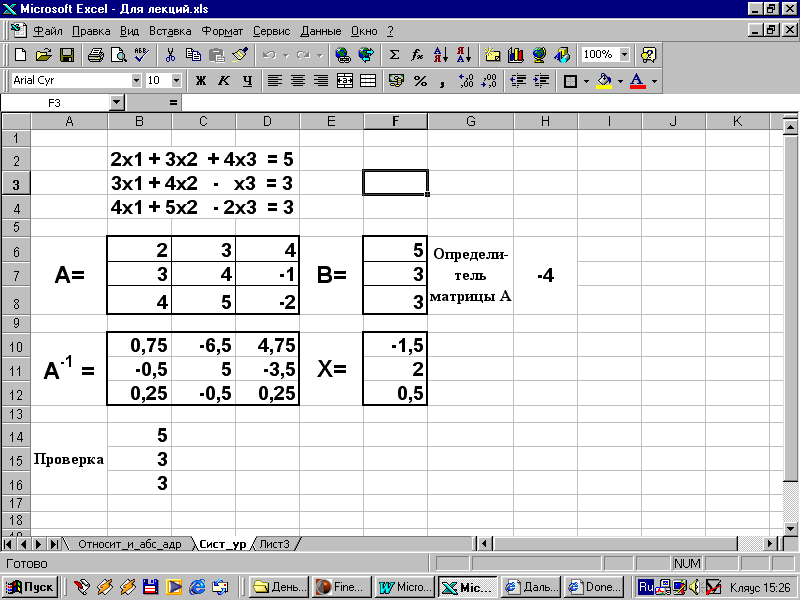
Решение системы линейных уравнений методом Крамера
Теперь рассмотрим решение системы линейных уравнений методом Крамера на примере следующей системы:
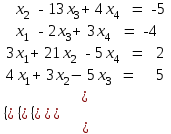 .
.
В этом случае матрица коэффициентов А и вектор свободных членов b имеют вид:
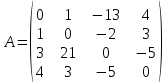 ,
, 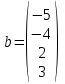 ,
,
Введём матрицу А и вектор b на второй рабочий лист. Кроме того, сформируем четыре матрицы из матрицы A заменой соответствующего столбца вектором b. Рабочий лист примет следующий вид:
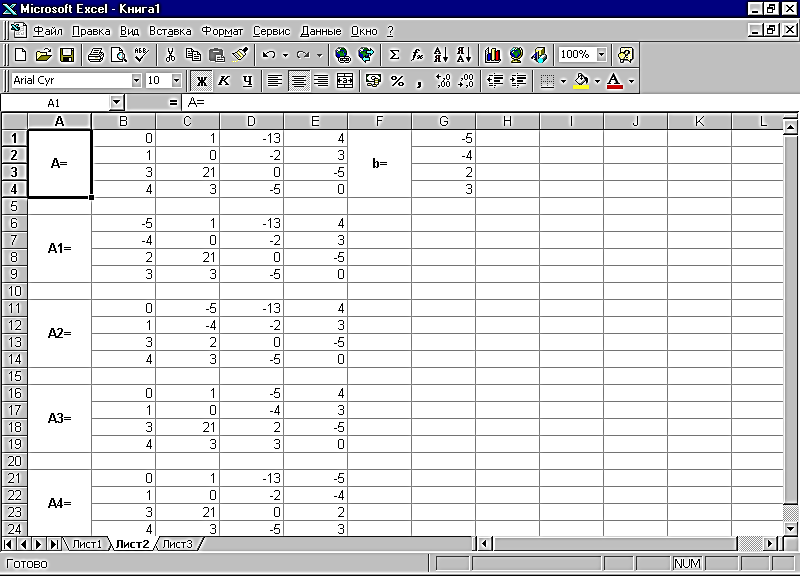
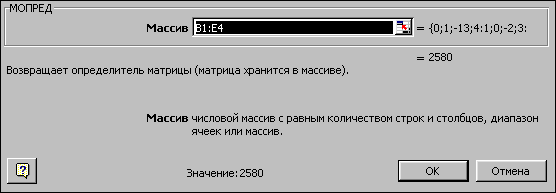
Теперь необходимо вычислить определители матриц A, A1 ,A2 ,A3 и A4. Определители в нашем случае будем хранить в ячейках I10–I14. Переведём курсор в ячейку I10 и обратимся к мастеру функций. В категории Математические выберем функцию МОПРЕД (это функция вычисления определителя матрицы), перейдём ко второму шагу мастера функций. В качестве параметра Массив укажем интервал B1:E4, где хранится матрица
A. В ячейки I11–I14 просто введем соответствующие формулы МОПРЕД(B6:E9), МОПРЕД(B11:E14), МОПРЕД(B16:E19), МОПРЕД(B21:E24).
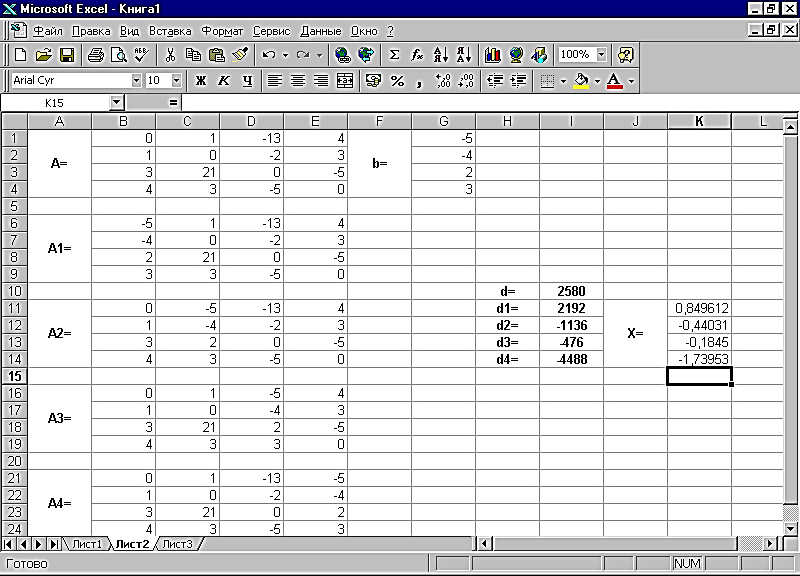
В результате мы вычислили все необходимые для решения системы определители. Осталось только разделить вспомогательные определители на основной, и мы решим систему уравнений. В ячейку K11 введём формулу =I11/$I$10. Затем скопируем её содержимое в ячейки K12, K13 и K14. Система решена. В результате рабочий лист имеет вид
Специальная вставка (пункт меню ПРАВКА)
Замена формулы ее значением


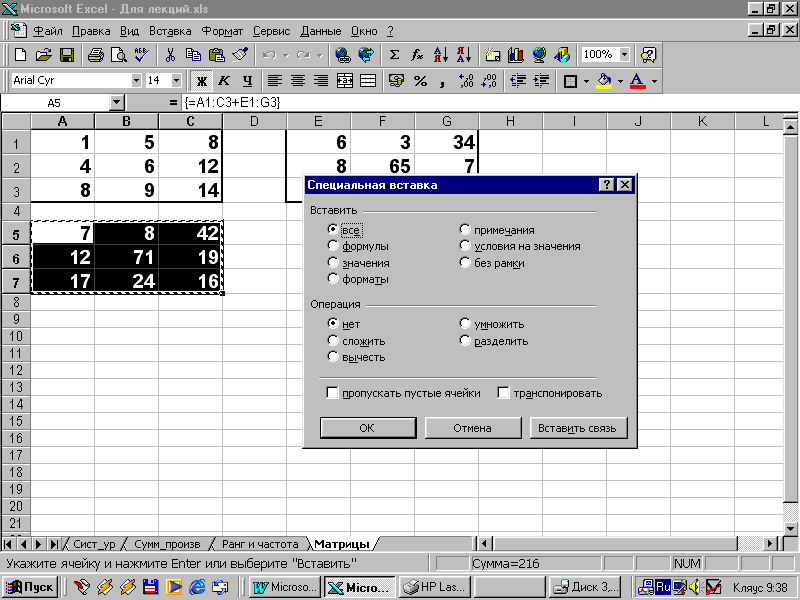
Формула заменится значением.
Используя Специальную вставку можно транспонировать данные.
Правила для формул массива:
-
Чтобы ввести формулу массива, сначала выделяется ячейка или диапазон ячеек, который будет содержать результат. -
Ввести формулу. Убедиться, что каждая ячейка аргумента содержит значение, которое должно быть использовано для вычисления операции или функции. -
Нажать CTRL+SHIFT+ENTER для фиксации ввода формулы массива. Необходимо удерживать нажатыми CTRL и SHIFT при нажатии ENTER.
Если действия выполнены правильно, EXCEL заключает формулу в фигурные скобки, указывая тем самым, что она является формулой массива. Не вводить фигурные скобки самим, т.к. EXCEL расценит это как ввод текстового значения.
Если удерживать нажатой только клавишу SHIFT, формула будет введена как обычная формула в активную ячейку.
Если удерживать нажатой только клавишу CTRL, формула будет введена как обычная формула во все выделенные ячейки.
-
Нельзя: редактировать, очищать или перемещать отдельные ячейки в диапазоне массива, а также вставлять или удалять ячейки. Ячейки в диапазоне массива рассматриваются как единое целое и редактировать их нужно все сразу.
Для изменения или чистки массива выделить весь массив и активизировать строку формул, при этом фигурные скобки вокруг формулы исчезнут. Изменить или очистить формулу, затем нажать CTRL+SHIFT+ENTER.
Чтобы выделить весь массив, щелкнуть по любой ячейке в массиве и нажать CTRL + /
Чтобы переместить содержимое диапазона массива, выделить весь массив, CTRL +X, затем выделить новый диапазон, CTRL +C, или перетащить выделенный диапазон в новое место.
Можно:
-
назначать разные форматы отдельным ячейкам в массиве -
копировать ячейки из диапазона массива и вставлять их в другие области рабочего листа
-
При работе с несколькими наборами массивов каждый набор должен иметь такое же число строк, как аргумент с наибольшим числом строк, и такое же число столбцов, как аргумент с наибольшим числом столбцов.
Пример 1. Сложить матрицы А1:С3 и Е1:G3
-
Выделить область под результат А5:С7 -
Ввести формулу = А1:С3 + Е1:G3 и нажать CTRL+SHIFT+ENTER
Аналогично выполняется вычитание матриц.
Пример 2. Умножение матрицы А1:С3 на коэффициент 1,5
-
Выделить область под результат А5:С7 -
Ввести формулу = 1,5*(А1:С3) и нажать CTRL+SHIFT+ENTER
Функции работы с матрицами
Категория Математические
МУМНОЖ(массив1,массив2,…) - умножение матриц
МОБР(массив) - нахождение обратной матрицы
МОПРЕД(массив) - вычисление определителя матрицы
Категория Ссылки и массивы
ИНДЕКС(массив) - извлечение из матрицы элемента по номеру строки и столбца
ЧСТРОК(массив), ЧИСЛСТОЛБ(массив) - определение числа строк и столбцов
ТРАНСП(массив) - транспонирование матрицы
Этапы выполнения умножения матриц с помощью МУМНОЖ:
-
Каждая из исходных матриц только в смежных ячейках -
Выделить диапазон ячеек для результирующей матрицы. При этом число строк результирующей матрицы равно числу строк первой матрицы, а число столбцов - числу столбцов второй матрицы. -
Вызвать мастер функций: Категория Математическая МУМНОЖ -
В окне диалога в поля аргументов ввести интервал ячеек, в которых располагаются матрицы (для каждого интервала - свое поле аргументов) -
Щелкнуть в строке формул или F2 и CTRL+SHIFT+ENTER.
В віделенной области появится результат произведения 2 матриц.
ТРАНСП - вместо матриц можно обрабатывать таблицы, включая заголовки. При выделении области для результата необходимо помнить, что число строк должно быть равно числу столбцов исходной матрицы, а число столбцов - числу строк исходной матрицы.
Решение системы линейных уравнений
Общий вид системы уравнений:
a11x1+a12x2+….+a1nxn=b1
………………………………
am1x1+am2x2+…amnxn=bm
Обозначим:
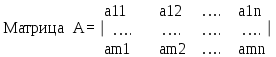
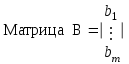
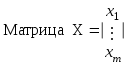
тогда можно записать систему уравнений в матричной форме:
А*Х=В,
для нахождения матрицы Х:
А-1*А*Х=А-1*В
т.е.
Х=А-1*В,
где А-1 - матрица, обратная матрице А.
Порядок решения системы уравнений:
-
Выписать коэффициенты при неизвестных в виде матрицы (матрица А), столбец свободных членов - в виде матрицы-столбца (матрица В) -
Найти определитель матрицы А с помощью МОПРЕД. Если определитель не равен нулю - есть решение системы уравнений -
Найти матрицу, обратную матрице А, с помощью МОБР:
-
Выделить ячейки для обратной матрицы (столько, сколько в матрице А). -
Мастер функций - Математические - МОБР (аргумент - ячейки матрицы А) и нажать CTRL+SHIFT+Enter (или нажать Ok, затем F2 и CTRL+SHIFT+Enter). Проверка правильности результата - перемножить обратную матрицу и матрицу А, результат - единичная матрица.
-
Умножить полученную обратную матрицу на матрицу В. Результат - матрица - столбец найденных неизвестных Х:
-
Выделить ячейки для матрицы Х (строк столько, сколько в матрице А, столбцов - сколько в матрице В). -
Мастер функций - Математические - МУМНОЖ (аргумент1 - ячейки обратной матрицы, аргумент 2 - матрица В) и нажать CTRL+SHIFT+Enter (или нажать Ok, затем F2 и CTRL+SHIFT+Enter).
-
Проверка правильности результата - перемножить матрицу А и матрицу Х, результат - матрица В.
Пример.
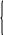
2х1 + 3х2 + 4х3 = 5
3х1 + 4х2 - х3 = 3
4х1 + 5х2 - 2х3 = 3

Решение системы линейных уравнений методом Крамера
Теперь рассмотрим решение системы линейных уравнений методом Крамера на примере следующей системы:
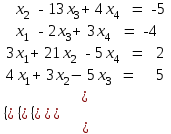 .
. В этом случае матрица коэффициентов А и вектор свободных членов b имеют вид:
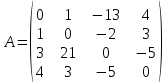 ,
, 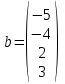 ,
,Введём матрицу А и вектор b на второй рабочий лист. Кроме того, сформируем четыре матрицы из матрицы A заменой соответствующего столбца вектором b. Рабочий лист примет следующий вид:

Теперь необходимо вычислить определители матриц A, A1 ,A2 ,A3 и A4. Определители в нашем случае будем хранить в ячейках I10–I14. Переведём курсор в ячейку I10 и обратимся к мастеру функций. В категории Математические выберем функцию МОПРЕД (это функция вычисления определителя матрицы), перейдём ко второму шагу мастера функций. В качестве параметра Массив укажем интервал B1:E4, где хранится матрица
A. В ячейки I11–I14 просто введем соответствующие формулы МОПРЕД(B6:E9), МОПРЕД(B11:E14), МОПРЕД(B16:E19), МОПРЕД(B21:E24).

В результате мы вычислили все необходимые для решения системы определители. Осталось только разделить вспомогательные определители на основной, и мы решим систему уравнений. В ячейку K11 введём формулу =I11/$I$10. Затем скопируем её содержимое в ячейки K12, K13 и K14. Система решена. В результате рабочий лист имеет вид

Специальная вставка (пункт меню ПРАВКА)
Замена формулы ее значением
-
Выделить исходные данные Буфер обмена Копировать



-
Буфер обмена Специальная вставка

-
Установить переключатель Значения

Формула заменится значением.
Используя Специальную вставку можно транспонировать данные.
-
Выделить исходные данные Буфер обмена Копировать -
Выделить одну ячейку, с которой начинается результирующий массив Буфер обмена Специальная вставка Транспонировать. -
Если исходные данные содержали формулы, установить переключатель Значения.