Файл: Расчет и проектирование вала, работающего в условиях многоциклового характера нагружения.docx

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования
«Пермский национальный исследовательский

политехнический университет»


Аэрокосмический факультет

кафедра «Механика композиционных материалов и конструкций»

направление 24.05.02 «Проектирование авиационных и ракетных двигателей»

О Т Ч Е Т

по курсовой работе на тему:
«Расчет и проектирование вала, работающего в условиях

многоциклового характера нагружения»

Вариант 0.7

Выполнил студент гр. АД-16-2с
Петров Кирилл Олегович
___________________________________________

(подпись)
Проверили:
доцент Макарова Елена Юрьевна

___________ _________________________

(оценка) (подпись)

_____________

(дата)
Пермь 2018

Содержание

Введение

Целью данной курсовой работы является расчёт вала на прочность при изгибе с кручением и на сопротивление многоцикловой усталости. В процессе выполнения проверяются навыки студента в расчёте вала, построении эпюр, способности оценивать полученные результаты с последующим применением их. Данная работа охватывает все темы, изученные за курс, поэтому следует повторить их. Вторая часть содержит материал, который подлежит самостоятельному изучению с использованием книг и других источники.

Полученные навыки являются базой инженера для проектирования конструкций типа стержень. При создании машин и узлов особо важно исключить ещё на этапе подготовки материала преждевременное разрушение детали. Для этого проводятся расчёты модели. Кроме того, ухудшению механических свойств материала могут способствовать участки деталей с концентрацией напряжений (резкое изменение сечения детали, технологические дефекты, в том числе дефекты материала металлургического происхождения, риски, царапины и т.п.), эксплуатация в недопустимых температурных режимах.

---

Разрушение деталей, работающих в условиях многократного циклического нагружения, происходит при напряжениях значительно меньших, чем при статическом нагружении. В настоящее время повышение предела выносливости достигается легированием и термической обработкой, а также улучшением конструктивных форм детали, повышением чистоты обработки поверхности и различными методами поверхностного упрочнения. Чем больше предел прочности детали, тем большее значение имеет повышение чистоты обработки поверхности и тем резче сказываются на уменьшении предела выносливости концентраторы напряжений: надрезы, резкие переходы сечений и др. Весьма значительное влияние на сопротивление усталости оказывают остаточные напряжения. В качестве методов поверхностного упрочнения для повышения предела выносливости находят широкое применение дробеструйный наклёп, обкатка роликами, химико-термическая обработка (цементизация, азотирование) и методы поверхностной закалки [1].

Исключив на этапе расчётов детали опасные сечения их упрочнением или выбором другого материала, можно существенно сократить расходы на разработку. Также при появлении новых материалов в машиностроении следует просчитать их механические свойства, чтобы дать оценку применимости. Данная работа не теряет своей актуальности с выходом на рынок новых программных пакетов для моделирования, так как в их основе лежат те же алгоритмы и расчёты, инженер должен знать, как они осуществляются.

1. Изгиб с кручением

Изгиб с кручением – частный случай сложного сопротивления, который может рассматриваться как сочетание чистого кручения и поперечного изгиба.

Основным критерием выбора материала является прочность. Прочность – это способность материала выдерживать определённую нагрузку не разрушаясь. Но также при создании учитываются и другие свойства. Для каждой детали, работающей в конкретных условиях, подбирается материал, отвечающий заданным параметрам. Расчёт осуществляется с начальными условиями, включающими в себя действующие силы, крутящие и изгибающие моменты, условия закрепления. Исходя из этого, строится модель и рассчитывается. При изгибе в поперечном сечении стержня действуют изгибающие моменты, плоскость действия которых перпендикулярна плоскости поперечного сечения. Эти моменты могут располагаться как в вертикальной, так и в горизонтальной плоскости, каждый случай считается отдельно, затем находится равнодействующий момент. Моменты, лежащие в плоскости сечения, называются крутящими. Если они возникают в поперечных сечениях стержня, то он испытывает кручение. Расчёт вала на прочность, подверженного действию моментов в трёх плоскостях, предстоит в данной работе.

---

К механическим характеристикам прочности относятся:

• 
  предел пропорциональности σ_пп (напряжение, до которого справедлив закон Гука);
  
• 
  предел упругости σ_у (напряжение, до которого материал работает упруго);
  
• 
  предел текучести σ_т (напряжение, при котором происходит рост деформации без увеличения силы);
  
• 
  предел прочности σ_пч (пороговая величина);
  
• 
  напряжение на разрыве.
  

1. 
   
   

Стержни, работающие на кручение, есть валы. По гипотезе Бернулли каждое поперечное сечение поворачивается на некоторый угол как жёсткое целое. Поэтому при кручении стержня в поперечных сечениях действуют только касательные напряжения, напряжённое состояние представляет собой чистый сдвиг. Крутящий момент сечения численно равен алгебраической сумме внешних скручивающих моментов, действующих по одну сторону от сечения. На оси стержня нагрузки нет: касательные напряжения прямопропорциональны расстоянию от центра тяжести сечения.

Характер распределения касательных напряжений по сечению устанавливается из геометрической картины деформации вала при кручении. Опыт показывает, что расстояния между сечениями скручиваемого вала не изменяются, а продольные линии предварительно нанесённой сетки принимают винтовую форму. При этом прямые углы искажаются, как и в случае чистого сдвига. Согласно экспериментальным данным, сечения плоские до деформации вала, остаются плоскими и после деформации, поворачиваясь одно относительно другого на некоторый угол. В этом смысл гипотезы плоских сечений, на основании которой строится вся элементарная теория кручения стержней [2].

При решении такого типа задач следует сначала определить все силы, действующие на вал, изгибающие и скручивающие моменты. Проверить правильность расчётов из условий, что суммы сил и моментов в каждой плоскости равны нулю. Составить схему нагружения. Разделить стержень на участки и построить эпюры действующих сил и моментов. Собственно, произвести расчёты.

Метод сечений используется для определения внутренних усилий. В данной работе с помощью него находятся реакции опор, а также строятся эпюры.

Этапы:

1. 
   Рассечь тело перпендикулярно его оси;
   
2. 
   Мысленно отбрасываем одну из частей;
   
3. 
   Прикладываем к сечению внутренние усилия;
   
4. 
   Записываем уравнения равновесия: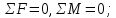
   
5. 
   Из уравнений находим неизвестные силы.
   

---

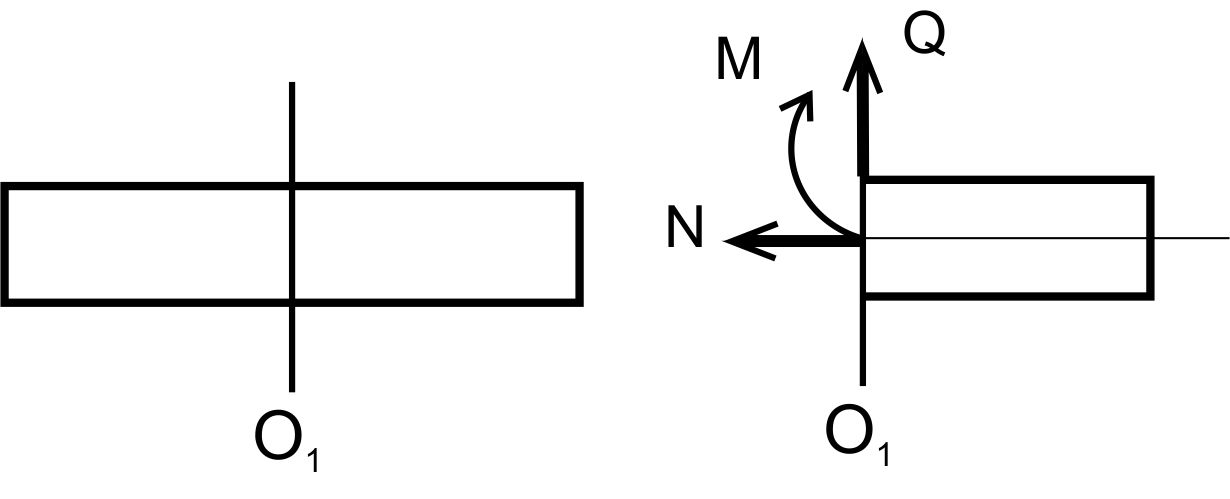
Рис. 1 - Метод сечений

Для расчёта требуемого диаметра следует выбрать опасное сечение вала. Опасными точками в сечении будут являться точки наиболее удаленные от нейтральной оси (для круглого сечения – линии, перпендикулярной плоскости действия результирующего изгибающего момента). При этом в точках сечения будет возникать плоское напряженное состояние, а потому расчет на прочность необходимо проводить с привлечением известных теорий прочности. Опасное сечение при кручении с изгибом устанавливается из совместного анализа эпюр крутящего M_z и полного изгибающего M_И моментов. Опасным будет считаться то сечение, где оба момента достигают своей максимальной величины. Если моменты достигают максимума в разных сечениях, необходимо проверить все сечения, в которых эти внутренние усилия достаточно велики.

Расчет на прочность вала при изгибе с кручением

Для ведущего вала прямозубой цилиндрической передачи редуктора с двумя зубчатыми колесами (рис. 4, а), передающего мощность Р, кВт, при

угловой скорости ω, рад/с,

1) определить вертикальные и горизонтальные составляющие реакций

подшипников;

2) построить эпюру крутящих моментов;

3) построить эпюры изгибающих моментов в вертикальной и горизонтальной

плоскостях;

4) определить диаметр вала из условия прочности, полагая Fr₁ = 0,4F₁; Fr₂ =

= 0,4F₂.

Исходные данные:

• 
  Марка стали – 40Х;
  
• 
  Допускаемый коэффициент запаса прочности [n] =1,8;
  
• 
  мощность, Р – 10 кВт;
  
• 
  угловая скорость, ω – 20 рад/с;
  
• 
  качество обработки поверхности – тонкое точение;
  
• 
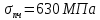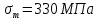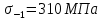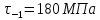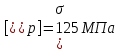  , , , , [1].
  

Решение.

1. 
   Составляем расчетную схему вала, приводя действующие на вал нагрузки к оси (рис. 4, б). При равномерном вращении вала M₁ = M₂, где M₁ и M₂ — скручивающие пары, которые добавляются при переносе сил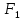 и 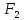на ось вала.
   
2. 
   Определяем вращающий момент, действующий на вал:
   

---

M₁=M₂=P/ω=10 ·10³H ·м / 20 рад/с = 0,5 кН·м.

3. 
   Вычислим нагрузки, приложенные к валу:
   

M=F·r, где F – приложенная сила, r – радиус колеса.

4. 
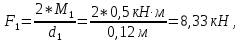
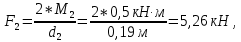
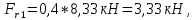
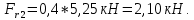
   Определяем реакции опор в вертикальной плоскости (рис. 4, б):
   

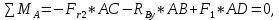
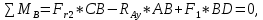
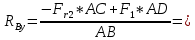
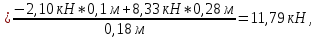
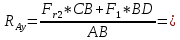
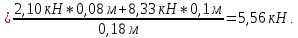
Выполним проверку:



,

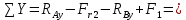
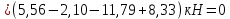следовательно, вертикальные реакции найдены верно:





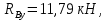
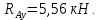
Направления сил указаны на схеме (рис. 4, б).

Определяем реакции опор в горизонтальной плоскости (рис. 4, б):










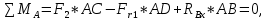
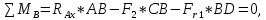
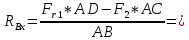
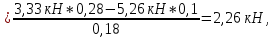
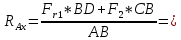
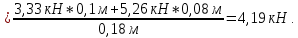
Выполним проверку:



,

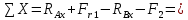
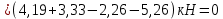следовательно, вертикальные реакции найдены верно:

5. 
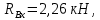
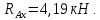
   Строим эпюру крутящих моментов М_z . С учётом правила знаков получаем эпюру (рис. 2).
   

1. 
   M_I = -M₂ = -0,5 кН*м;
   
2. 
   M_II = -M₁ = -0,5 кН*м.
   

---