Файл: Контрольная работа по дисциплине Метрология и техническое регулирование Вариант 1 Ибрагимов Р. М. Группа.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 81
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М. А. БОНЧ-БРУЕВИЧА»
(СПбГУТ)
Институт непрерывного образования
Метрология, стандартизация и сертификация в инфокоммуникациях
Контрольная работа по дисциплине Метрология и техническое регулирование Вариант 1
Выполнил: Ибрагимов Р.М.
Группа:
САНКТ-ПЕТЕРБУРГ 2023
Задача 1. ЭЛЕМЕНТЫ ТЕОРИИ ПОГРЕШНОСТЕЙ [1, с. 6-15, 60-83]; [2, с. 5-13, 35-53]
В целях исследования характеристик генератора, номинальная частота которого f0= 22700 Гц, при неизменных внешних условиях получен ряд независимых измерений его частоты:
| № | 1 | 2 | 3 | 4 | 5 | 6 |
| f, Гц | 22645 | 22611 | 22678 | 22621 | 22621 | 22625 |
Определите:
− систематическую и случайные составляющие погрешности частоты исследуемого генератора в предположении, что флуктуации частоты генератора имеют нормальный закон распределения;
− рассчитайте оценку среднего значения частоты по данному ряду наблюдений и ее доверительный интервал при доверительной вероятности 0,95.
Можно ли считать доказанным наличие систематической погрешности частоты у
данного генератора?
Решение:
Систематическая погрешность определяется как отклонение результата измерений (т.е. среднего арифметического) от действительного значения измеряемой физической величины f0= 22700 Гц:
∆????сис = ????0−????ср (1)
Определим среднее значение частоты по формуле
 ∑????????
∑????????????ср = ????
(2)
????ср =
22645 + 22611 + 22678 + 22621 + 22621 + 22625

6
= 22633,5 Г
Найдем отклонения случайной величины от среднего значения:
????1 − ????ср = 22645 − 22633,5 = 11,5 Гц
????2 − ????ср = 22611 − 22633,5 = −22,5 Гц
????3 − ????ср = 22678 − 22633,5 = 44,5 Гц
????4 − ????ср = 22621 − 22633,5 = −12,5 Гц
????5 − ????ср = 22621 − 22633,5 = −12,5 Гц
????6 − ????ср = 22625 − 22633,5 = −8,5 Гц
Найдем сумму отклонений:
∑(???????? − ????ср) = 11,5 − 22,5 + 44,5 − 12,5 − 12,5 − 8,5 = 0
Сумма отклонения равна нулю, следовательно среднее значение вычислено верно.
Систематическая составляющая погрешности частоты исследуемого генератора по (1):
∆????сис = 22700 − 22633,5 = 66,5 Гц
Случайная погрешность выражается доверительным интервалом ε, который вычисляется по формуле:
ε = ts(0,95; 6)
∙ ????(????) (3)
где tS(P;n) — коэффициент Стьюдента для n измерений при доверительной вероятности Р = 0,95;
S(f) − средняя квадратическая погрешность результата измерения.
Средняя квадратическая погрешность результата измерения определяется формулой ([1], 4.30):
????
 ????(????) =
????(????) = √????
(4)
где S −среднеквадратичное отклонение погрешности результата наблюдений (стандартной неопределенности единичного измерения);
n – число измерений.
Среднеквадратичное отклонение погрешности результата наблюдений
(стандартной неопределенности единичного измерения) найдем по формуле ([1] 4.23):

2
 ???? = √∑(???????? − ????ср)
???? = √∑(???????? − ????ср)???? − 1
Найдем сумму квадратов отклонений:
(5)
∑(???????? − ????ср)2 = 11,52 + 22,52 + 44,52 + 12,52 + 12,52 + 8,52 = 3003,5

Среднеквадратичное отклонение погрешности результата наблюдений по (5):
3003,5
 ???? = √
???? = √6 − 1
= 24,51 Гц
Определим среднюю квадратическую погрешность результата измерения по (4):
????(????) =
24,51

√6
= 10 Гц
Коэффициент Стьюдента для 6 измерений при доверительной вероятности Р = 0,95
tS(0,95;6) = 2,5706
Границы доверительного интервала погрешности по (3):
ε = 2,5706 ∙ 10 = 25,71 Гц
Оставим в погрешности результата 2 значащие цифры.
ε = 26 Гц
Как видно, систематическая погрешность ∆????сис больше доверительного интервала ε, что доказывает существование систематической погрешности.
Результат измерения в соответствии с правилами представления результата МИ 1317-2004 запишем следующим образом:
f= (22634 ± 26 + 66,5) Гц; Рf= 0,95; n = 6
Задача 2. ИЗМЕРЕНИЕ ТОКА И НАПРЯЖЕНИЯ [1, с. 21-43, 85-110]; [2, с. 30-34, 47-48, 54-109]
Магнитоэлектрическим миллиамперметром класса точности 0,5 на пределе 1 мА измеряют ток периодического сигнала, форма которого показана на рис. 1.
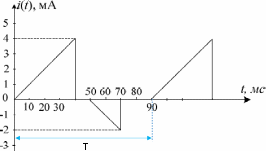
Рис. 2.1 Форма исследуемого напряжения.
Определите показания прибора, оцените абсолютную и относительную погрешности измерения, запишите в соответствии с правилами результат измерения. Какое значение тока измеряет такой прибор? Определите показания выпрямительного миллиамперметра класса точности 1,5 при измерении этого же сигнала на пределе 2,5 мА. Запишите результат измерения вместе с оценкой абсолютной погрешности.
Решение:
Магнитоэлектрические приборы измеряют среднее значение (постоянную составляющую) сигнала. Определенный интеграл дает площадь, ограниченную графиком исследуемой функции, таким образом, показания шкалы магнитоэлектрического амперметра [1, с. 27, ф.3.1]:
Т
1
 ????0 = Т ∫ ????(????)???????? (1)
????0 = Т ∫ ????(????)???????? (1)0
Запишем аналитическое выражение сигнала в пределах одного периода.
0,1????, 0 < ???? < 40 мс
????(????) = { 0, 40 < ???? < 50 мс
−0,1(???? − 50), 50 < ???? < 70 мс
0, 70 < ???? < 90 мс
Подставляя аналитическое выражение данного сигнала, получаем:
40 70
1
0,1 ????2 40
 ????2 70
????2 70

 ????0 = 90 (∫ 0,1???????????? − ∫ 0,1(???? − 50)????????
????0 = 90 (∫ 0,1???????????? − ∫ 0,1(???? − 50)????????) = 90 ( 2 | 0
− ( 2 − 50????) |50) =
0
 0,1 402
0,1 40250
702
 502
502
 = 90 (
= 90 (2 − ( 2 −
2 − 50 ∙ (70 − 50))) = 0,666 мА
Выпрямительный прибор показывает средневыпрямленное значение.
Т
40 70
1
 ????св = Т ∫|????(????)|???????? (2)
????св = Т ∫|????(????)|???????? (2)0
1
 ????св = 90 (∫ 0,1???????????? + ∫ 0,1(???? − 50)????????
????св = 90 (∫ 0,1???????????? + ∫ 0,1(???? − 50)????????0,1
 ) = 90
) = 90????2 40
 ( 2 | 0
( 2 | 0????2
 + ( 2
+ ( 2− 50????) |
70
50) =
0
 0,1 402
0,1 40250
702
 502
502
 = 90 (
= 90 (2 + ( 2 −
2 − 50 ∙ (70 − 50))) = 1,111 мА