Файл: 11 Общие сведения о комплексных соединениях 11 Состав комплексных соединений.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 128
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Координационные числа >6 встречаются достаточно редко. Координационные числа 8 и более (вплоть до 15) характерны для катионов лантаноидов, актиноидов и некоторых других элементов с большим радиусом. В ионных соединениях этих элементов координационный многогранник (полиэдр) — куб, а в комплексах — додекаэдр (d 4sp3гидридизация), квадратная антипризма (d 4sp3- или d5p3-гибридизация) и т. д. Примеры соединений с большими координационными числами — [Ln(H2O)9]3 (Ln — лантаноид); [MH9]2– (M = Tc, Re; КЧ = 9); [Ce(NO3)5]2– (КЧ = 10); [Ce(NO3)6]3– (КЧ = 12). В двух последних комплексах лиганды бидентатные.
Рассмотрим образование некоторых комплексов с позиций теории валентных связей. Например, катион тетраамминцинка(II) [Zn(NH3)4]2 включает комплексообразователь цинк(II). Электронная оболочка этого условного иона имеет конфигурацию [Ar]3d104s04p0, которую можно изобразить следующим образом:
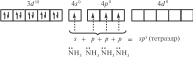
Вакантные 4s- и 4p-орбитали атома цинка(II) образуют четыре sp3гибридные орбитали, направленные к вершинам тетраэдра. Каждая молекула аммиака имеет на атоме азота неподеленную пару электронов. Орбитали атомов азота, которые содержат неподеленные пары электронов, перекрываются с sp3-гибридными орбиталями цинка(II), образуя тетраэдрический комплексный катион. Таким образом, в ионе [Zn(NH3)4]2 нет неспаренных электронов — он диамагнитен.
Марганец(II) в составе тетрахлороманганат(II)-иона [MnCl4]2– содержит пять неспаренных электронов на 3d-орбиталях, а также вакантные 4s- и 4p-орбитали. Вакантные sp3-гибридные орбитали марганца(II) перекрываются с p-орбиталями хлорид-ионов:

Тетраэдрический ион [MnCl4]2– парамагнитен (содержит пять неспаренных электронов).
Во многих случаях метод валентных связей не позволяет предсказать тип гибридизации и геометрическую форму комплексной частицы без знания ее магнитных свойств. Например, правильно определить тип гибридизации атомных орбиталей комплексообразователя в соединениях [Ni(CO)4], [Ni(CN)4]2– и [NiBr4]2– можно, только зная, что первые две частицы диамагнитны, а третья парамагнитна.
Для [Ni(CO)4] необходимо учесть отсутствие неспаренных электронов. Нейтральный атом никеля парамагнитен:
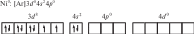
Переход 4s-электронов на 3d-подуровень превращает парамагнитный атом Ni0 в возбужденную диамагнитную частицу Ni*:
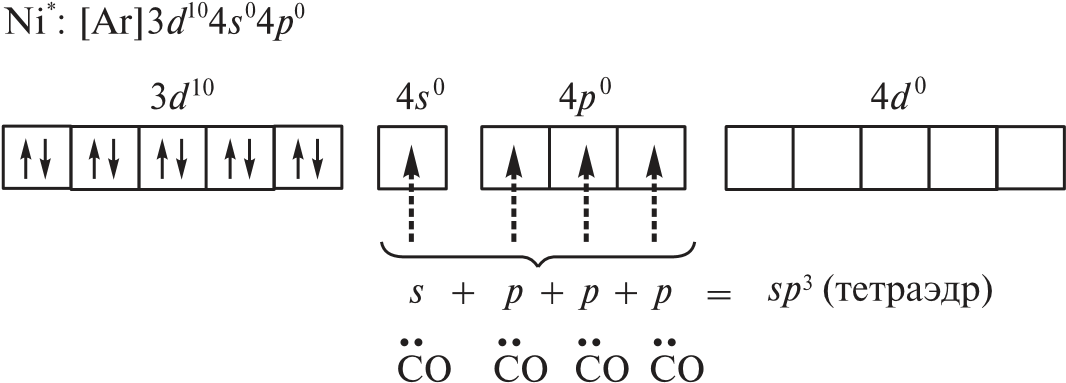
Освободившиеся вакантные орбитали подвергаются sp3-гибридизации, в результате образуется устойчивый тетраэдрический комплекс тетракарбонилникель (КЧ = 4).
В парамагнитном [NiBr4]2– комплексообразователем служит никель(II) с электронной конфигурацией [Ar]3d 84s04p0, у которого для реализации КЧ = 4 достаточно вакантных орбиталей:
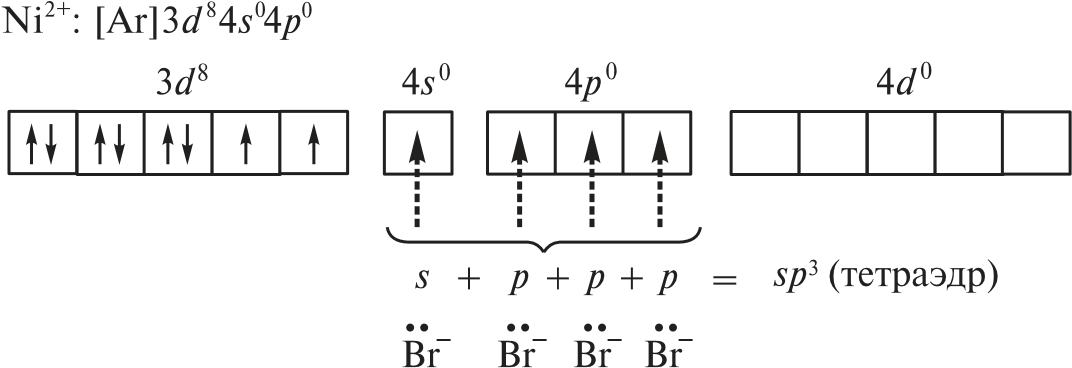
Таким образом, парамагнитный комплекс [NiBr4]2– также имеет тетраэдрическое строение, но гораздо менее устойчив, чем [Ni(CO)4].
При объединении двух электронов 3d-подуровня иона никеля(II) в пару и превращении одной из орбиталей этого подуровня в вакантную изменяется тип гибридизации и образуется устойчивый диамагнитный комплекс [Ni(CN)4]2– (КЧ = 4) — тип гибридизации dsp2, которому соответствует плоскоквадратная форма частицы.
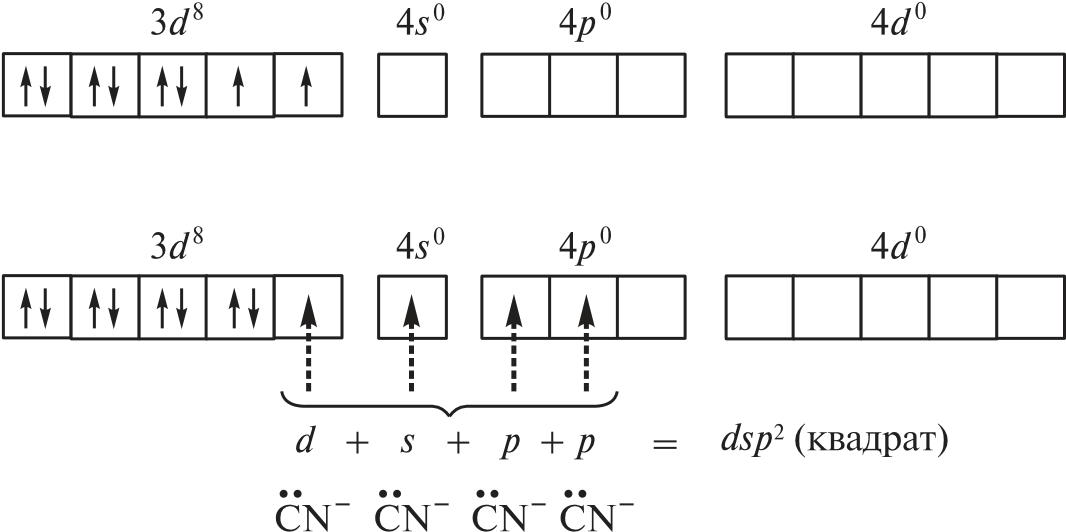

| | | | | |
Если синтез осуществляется в условиях избытка лиганда, координационное число никеля(II) равно пяти (dsp3-гибридизация) и формируется устойчивый диамагнитный комплекс [Ni(CN)5]3–, который имеет форму квадратной пирамиды.
Октаэдрический комплекс никеля(II) [Ni(H2O)6]2 парамагнитен, но достаточно устойчив. В нем реализуется sp3d2-гибридизация атомных орбиталей никеля(II):

Если в гибридизации участвуют атомные орбитали внешнего d-подуровня комплексообразователя (например, при sp3d2- или sp3d-гибриди зации), комплекс называют внешнеорбитальным. Комплексы, при образовании которых в гибридизации участвуют атомные орбитали предпоследнего
d-подуровня (тип гибридизации, например, d 2sp3 или dsp2), называют внутриорбитальными.
Железо(II) образует и внешне-, и внутриорбитальные комплексы, например парамагнитный внешнеорбитальный гексафтороф еррат(II)-ион [FeF6]4– и диамагнитный внутриорбитальный гексациано феррат(II)-ион [Fe(CN)6]4–.
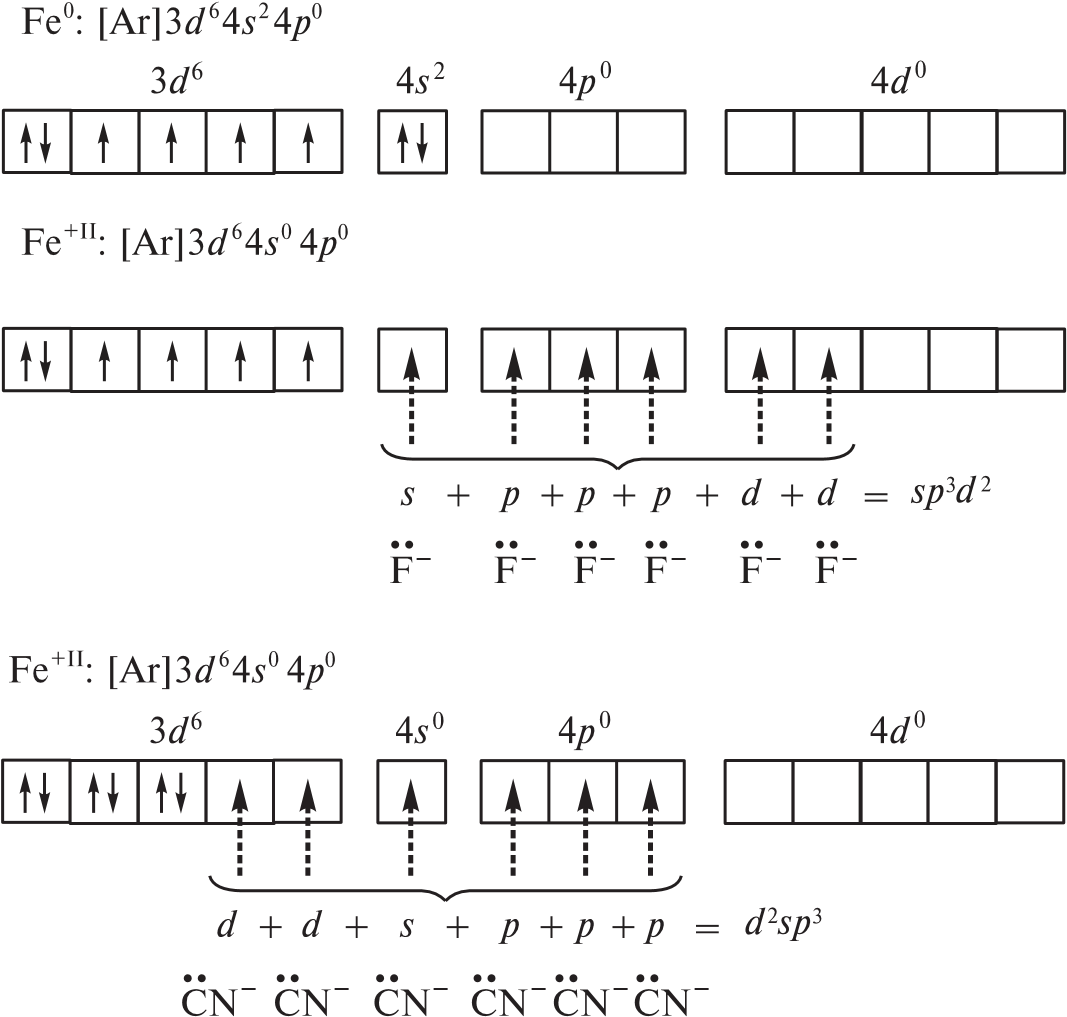
Фторид- и цианид-ионы как лиганды по-разному влияют на электроны валентных уровней атома железа. Теория валентных связей не учитывает природу лиганда, поэтому методом ВС невозможно предсказать строение таких комплексов. Таким образом, метод ВС необходимо дополнять данными о магнитных свойствах комплексного соединения и о влиянии лиганда.
Вопросы
11.10. Перечислите достоинства и недостатки метода валентных связей (ВС) (применительно к комплексным соединениям).
11.11. Определите диамагнитные и парамагнитные комплексы:
а) [Co(NH3)6]3; б) [TiF6]3–; в) [TiCl6]2–; г) [CuCl5]3–; д) [Cu(OH)6]4–;
е) [V(H2O)6]3; ж) [VCl4]–; з) [VF6]–; и) [Cu(CN)4]2–.
11.4.2. Теория кристаллического поля
Для предсказания строения комплексных соединений d-элементов хорошим дополнением к методу валентных связей оказалась теория кристаллического поля (КП). Основы этой теории были разработаны Бете в 1929 г. при рассмотрении эффекта замещения катиона натрия в решетке ионного кристалла типа NaCl. Бете показал, что при помещении свободного иона в электростатическое поле (так называемое кристаллическое поле), существующее в кристалле, происходит полное или частичное снятие вырождения энергетических подуровней иона, т. е. их расщепление.
Согласно теории кристаллического поля, вокруг положительно заряженного центрального иона упорядоченно располагаются точечные лиганды, которые заряжены отрицательно. Число этих точечных отрицательных зарядов определяет симметрию системы (комплекса). Реальный объем лигандов, а также их геометрическое и электронное строение во внимание не принимаются. Взаимодействие центрального атома с лигандами рассматривается с позиций квантовой механики. Энергия свободного (несвязанного) иона определяется кинетической энергией системы, энергией взаимодействия электрона с ядром, а также энергией межэлектронного и спин-орбитального взаимодействия6. При помещении иона в кристаллическое поле той или иной геометрии, которая зависит от симметрии системы в целом, на энергию системы дополнительно влияет потенциал V кристаллического поля. В теории кристаллического поля чаще рассматривают поля октаэдрической и тетраэдрической симметрии.
В поле сферической симметрии все орбитали d-подуровня свободных ионов переходных металлов вырождены (имеют одинаковую энергию). В электростатическом поле более низкой симметрии d-орбитали неэквивалентны по энергии (происходит расщепление подуровней, т. е. частичное снятие вырождения энергии). Расщепление подуровней в поле октаэдрической симметрии показано на рис. 11.10. Атомные dJ-орбитали (dx2−y2 и dz2 ) симметрии eg ближе всего подходят к орбиталям лигандов и подвер-

Рис. 11.10. Расщепление d-подуровня в кристаллическом поле октаэдрической симметрии гаются наиболее сильному воздействию их электростатического поля. Возникновение сил отталкивания приводит к увеличению энергии egорбиталей (они дестабилизируются). Три другие d-АО (dху, dxz, dyz) симметрии t2g, называемые dH, располагаются между орбиталями лигандов, поэтому их энергия понижается (орбитали стабилизируются).
Разность энергий eg- и t2g-состояний часто обозначают7 как 10Dq. Dq — это радиальный интеграл, который зависит от эффективного заряда и порядкового номера центрального иона Mn+, а также от расстояния металл—лиганд. В спектроскопии неорганических соединений величину Dq обычно называют основным параметром расщепления электронных конфигураций.
Характер расщепления определяется симметрией кристаллического поля и числом d-электронов иона переходного металла. Большое значение имеет также тип кристаллического поля, который зависит от природы лигандов. Чем сильнее поле лигандов, тем больше энергия расщепления. Обычно рассматривают два крайних случая — слабое и сильное кристаллические поля.
В слабом поле потенциал межэлектронного взаимодействия существенно больше потенциала кристаллического поля и, тем более, потенциала спин-орбитального взаимодействия. Координационные соединения с лигандами, создающими слабые кристаллические поля, называют высокоспиновыми (в методе ВС такие соединения называют спин-свободными (внешнеорбитальными) или ионными комплексами).
В сильном поле потенциал V заметно превышает потенциалы межэлектронного и спин-орбитального взаимодействий и поэтому подавляет их. Координационные соединения с лигандами, создающими сильные кристаллические поля, называют низкоспиновыми (в методе ВС им соответствуют спин-связанные (внутриорбитальные) или ковалентные комплексы).
В зависимости от силы поля лигандов заселение орбиталей электронами происходит по-разному. В слабом поле, в соответствии с правилом Хунда, сначала (t2g- и eg-орбитали) последовательно заселяются одним электроном, и лишь после этого начинается заселение вторыми электронами наиболее низких по энергии t2g-орбиталей (рис. 11.11). В сильном поле прежде всего полностью заселяются t2g-орбитали, а уже потом eg-орбитали.
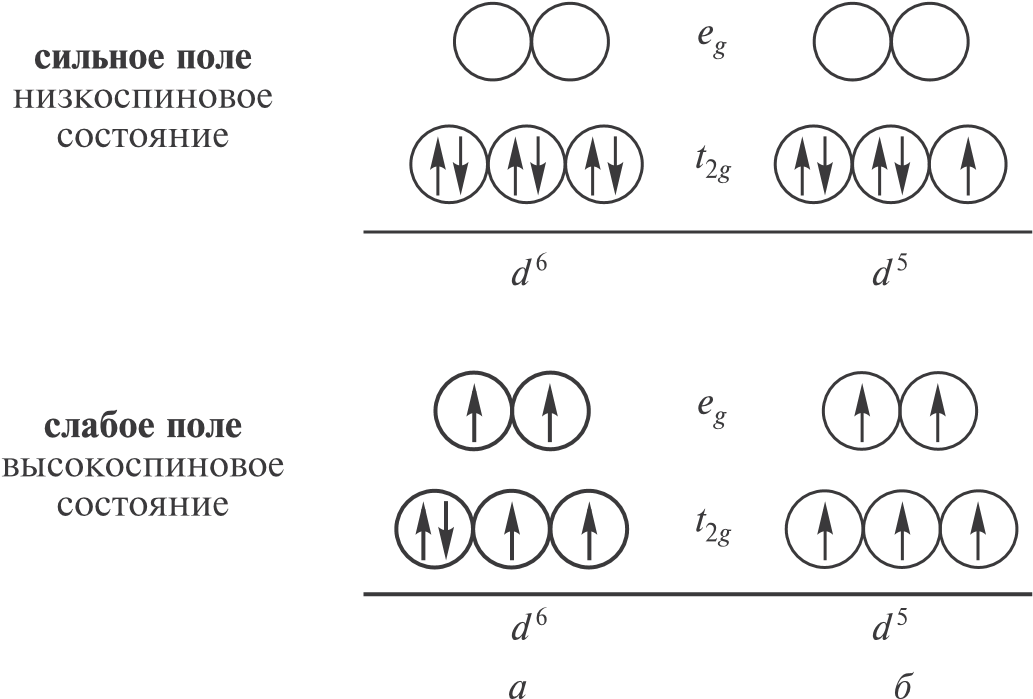
Рис. 11.11. Заселение орбиталей электронами в сильном (а) и слабом (б) тетраэдрических кристаллических полях на примере d 5- и d 6-конфигураций
Соответствующие энергетические состояния характеризуют через заселенности t2g- и еg-орбиталей (например, t e25g g0).
При eg–t2g-расщеплении энергия eg-орбиталей (и их электронов) повышается на 6Dq, а энергия t2g-орбиталей понижается на 4Dq. В итоге энергия системы в целом уменьшается; этот энергетический выигрыш называют энергией стабилизации кристаллическим полем8 (ЭСКП, обозначается δ). Величина ЭСКП зависит от числа электронов на eg- и t2gорбиталях и во многом определяет главные свойства комплексного соединения.
Для октаэдрического поля ЭСКП (δ) рассчитывается по формуле:
δ = n(4Dq) – m(6Dq)
где n — число электронов на t2g-подуровне, m — число электронов на egподуровне. Например, ЭСКП для конфигурации t e23g g0:
δ = (4Dq) ⋅ 3 = 12Dq
а для конфигурации t e23g g2:
δ = (4Dq) ⋅ 3 – (6Dq) ⋅ 2 = 0
В случае сильного поля расчет аналогичен, однако необходимо учитывать иной порядок заполнения орбиталей, например для ЭСКП конфигу-
рации t e25g g0:
δ = (4Dq) ⋅ 5 = 20Dq
Таблица 11.2
Значения ЭСКП (Dq) для разных октаэдрических комплексов
Вопросы
11.10. Перечислите достоинства и недостатки метода валентных связей (ВС) (применительно к комплексным соединениям).
11.11. Определите диамагнитные и парамагнитные комплексы:
а) [Co(NH3)6]3; б) [TiF6]3–; в) [TiCl6]2–; г) [CuCl5]3–; д) [Cu(OH)6]4–;
е) [V(H2O)6]3; ж) [VCl4]–; з) [VF6]–; и) [Cu(CN)4]2–.
11.4.2. Теория кристаллического поля
Для предсказания строения комплексных соединений d-элементов хорошим дополнением к методу валентных связей оказалась теория кристаллического поля (КП). Основы этой теории были разработаны Бете в 1929 г. при рассмотрении эффекта замещения катиона натрия в решетке ионного кристалла типа NaCl. Бете показал, что при помещении свободного иона в электростатическое поле (так называемое кристаллическое поле), существующее в кристалле, происходит полное или частичное снятие вырождения энергетических подуровней иона, т. е. их расщепление.
Согласно теории кристаллического поля, вокруг положительно заряженного центрального иона упорядоченно располагаются точечные лиганды, которые заряжены отрицательно. Число этих точечных отрицательных зарядов определяет симметрию системы (комплекса). Реальный объем лигандов, а также их геометрическое и электронное строение во внимание не принимаются. Взаимодействие центрального атома с лигандами рассматривается с позиций квантовой механики. Энергия свободного (несвязанного) иона определяется кинетической энергией системы, энергией взаимодействия электрона с ядром, а также энергией межэлектронного и спин-орбитального взаимодействия6. При помещении иона в кристаллическое поле той или иной геометрии, которая зависит от симметрии системы в целом, на энергию системы дополнительно влияет потенциал V кристаллического поля. В теории кристаллического поля чаще рассматривают поля октаэдрической и тетраэдрической симметрии.
В поле сферической симметрии все орбитали d-подуровня свободных ионов переходных металлов вырождены (имеют одинаковую энергию). В электростатическом поле более низкой симметрии d-орбитали неэквивалентны по энергии (происходит расщепление подуровней, т. е. частичное снятие вырождения энергии). Расщепление подуровней в поле октаэдрической симметрии показано на рис. 11.10. Атомные dJ-орбитали (dx2−y2 и dz2 ) симметрии eg ближе всего подходят к орбиталям лигандов и подвер-

Рис. 11.10. Расщепление d-подуровня в кристаллическом поле октаэдрической симметрии гаются наиболее сильному воздействию их электростатического поля. Возникновение сил отталкивания приводит к увеличению энергии egорбиталей (они дестабилизируются). Три другие d-АО (dху, dxz, dyz) симметрии t2g, называемые dH, располагаются между орбиталями лигандов, поэтому их энергия понижается (орбитали стабилизируются).
Разность энергий eg- и t2g-состояний часто обозначают7 как 10Dq. Dq — это радиальный интеграл, который зависит от эффективного заряда и порядкового номера центрального иона Mn+, а также от расстояния металл—лиганд. В спектроскопии неорганических соединений величину Dq обычно называют основным параметром расщепления электронных конфигураций.
Характер расщепления определяется симметрией кристаллического поля и числом d-электронов иона переходного металла. Большое значение имеет также тип кристаллического поля, который зависит от природы лигандов. Чем сильнее поле лигандов, тем больше энергия расщепления. Обычно рассматривают два крайних случая — слабое и сильное кристаллические поля.
В слабом поле потенциал межэлектронного взаимодействия существенно больше потенциала кристаллического поля и, тем более, потенциала спин-орбитального взаимодействия. Координационные соединения с лигандами, создающими слабые кристаллические поля, называют высокоспиновыми (в методе ВС такие соединения называют спин-свободными (внешнеорбитальными) или ионными комплексами).
В сильном поле потенциал V заметно превышает потенциалы межэлектронного и спин-орбитального взаимодействий и поэтому подавляет их. Координационные соединения с лигандами, создающими сильные кристаллические поля, называют низкоспиновыми (в методе ВС им соответствуют спин-связанные (внутриорбитальные) или ковалентные комплексы).
В зависимости от силы поля лигандов заселение орбиталей электронами происходит по-разному. В слабом поле, в соответствии с правилом Хунда, сначала (t2g- и eg-орбитали) последовательно заселяются одним электроном, и лишь после этого начинается заселение вторыми электронами наиболее низких по энергии t2g-орбиталей (рис. 11.11). В сильном поле прежде всего полностью заселяются t2g-орбитали, а уже потом eg-орбитали.

Рис. 11.11. Заселение орбиталей электронами в сильном (а) и слабом (б) тетраэдрических кристаллических полях на примере d 5- и d 6-конфигураций
Соответствующие энергетические состояния характеризуют через заселенности t2g- и еg-орбиталей (например, t e25g g0).
При eg–t2g-расщеплении энергия eg-орбиталей (и их электронов) повышается на 6Dq, а энергия t2g-орбиталей понижается на 4Dq. В итоге энергия системы в целом уменьшается; этот энергетический выигрыш называют энергией стабилизации кристаллическим полем8 (ЭСКП, обозначается δ). Величина ЭСКП зависит от числа электронов на eg- и t2gорбиталях и во многом определяет главные свойства комплексного соединения.
Для октаэдрического поля ЭСКП (δ) рассчитывается по формуле:
δ = n(4Dq) – m(6Dq)
где n — число электронов на t2g-подуровне, m — число электронов на egподуровне. Например, ЭСКП для конфигурации t e23g g0:
δ = (4Dq) ⋅ 3 = 12Dq
а для конфигурации t e23g g2:
δ = (4Dq) ⋅ 3 – (6Dq) ⋅ 2 = 0
В случае сильного поля расчет аналогичен, однако необходимо учитывать иной порядок заполнения орбиталей, например для ЭСКП конфигу-
рации t e25g g0:
δ = (4Dq) ⋅ 5 = 20Dq
Таблица 11.2
Значения ЭСКП (Dq) для разных октаэдрических комплексов
Вопросы
11.10. Перечислите достоинства и недостатки метода валентных связей (ВС) (применительно к комплексным соединениям).
11.11. Определите диамагнитные и парамагнитные комплексы:
а) [Co(NH3)6]3; б) [TiF6]3–; в) [TiCl6]2–; г) [CuCl5]3–; д) [Cu(OH)6]4–;
е) [V(H2O)6]3; ж) [VCl4]–; з) [VF6]–; и) [Cu(CN)4]2–.
11.4.2. Теория кристаллического поля
Для предсказания строения комплексных соединений d-элементов хорошим дополнением к методу валентных связей оказалась теория кристаллического поля (КП). Основы этой теории были разработаны Бете в 1929 г. при рассмотрении эффекта замещения катиона натрия в решетке ионного кристалла типа NaCl. Бете показал, что при помещении свободного иона в электростатическое поле (так называемое кристаллическое поле), существующее в кристалле, происходит полное или частичное снятие вырождения энергетических подуровней иона, т. е. их расщепление.
Согласно теории кристаллического поля, вокруг положительно заряженного центрального иона упорядоченно располагаются точечные лиганды, которые заряжены отрицательно. Число этих точечных отрицательных зарядов определяет симметрию системы (комплекса). Реальный объем лигандов, а также их геометрическое и электронное строение во внимание не принимаются. Взаимодействие центрального атома с лигандами рассматривается с позиций квантовой механики. Энергия свободного (несвязанного) иона определяется кинетической энергией системы, энергией взаимодействия электрона с ядром, а также энергией межэлектронного и спин-орбитального взаимодействия6. При помещении иона в кристаллическое поле той или иной геометрии, которая зависит от симметрии системы в целом, на энергию системы дополнительно влияет потенциал V кристаллического поля. В теории кристаллического поля чаще рассматривают поля октаэдрической и тетраэдрической симметрии.
В поле сферической симметрии все орбитали d-подуровня свободных ионов переходных металлов вырождены (имеют одинаковую энергию). В электростатическом поле более низкой симметрии d-орбитали неэквивалентны по энергии (происходит расщепление подуровней, т. е. частичное снятие вырождения энергии). Расщепление подуровней в поле октаэдрической симметрии показано на рис. 11.10. Атомные dJ-орбитали (dx2−y2 и dz2 ) симметрии eg ближе всего подходят к орбиталям лигандов и подвер-

Рис. 11.10. Расщепление d-подуровня в кристаллическом поле октаэдрической симметрии гаются наиболее сильному воздействию их электростатического поля. Возникновение сил отталкивания приводит к увеличению энергии egорбиталей (они дестабилизируются). Три другие d-АО (dху, dxz, dyz) симметрии t2g, называемые dH, располагаются между орбиталями лигандов, поэтому их энергия понижается (орбитали стабилизируются).
Разность энергий eg- и t2g-состояний часто обозначают7 как 10Dq. Dq — это радиальный интеграл, который зависит от эффективного заряда и порядкового номера центрального иона Mn+, а также от расстояния металл—лиганд. В спектроскопии неорганических соединений величину Dq обычно называют основным параметром расщепления электронных конфигураций.
Характер расщепления определяется симметрией кристаллического поля и числом d-электронов иона переходного металла. Большое значение имеет также тип кристаллического поля, который зависит от природы лигандов. Чем сильнее поле лигандов, тем больше энергия расщепления. Обычно рассматривают два крайних случая — слабое и сильное кристаллические поля.
В слабом поле потенциал межэлектронного взаимодействия существенно больше потенциала кристаллического поля и, тем более, потенциала спин-орбитального взаимодействия. Координационные соединения с лигандами, создающими слабые кристаллические поля, называют высокоспиновыми (в методе ВС такие соединения называют спин-свободными (внешнеорбитальными) или ионными комплексами).
В сильном поле потенциал V заметно превышает потенциалы межэлектронного и спин-орбитального взаимодействий и поэтому подавляет их. Координационные соединения с лигандами, создающими сильные кристаллические поля, называют низкоспиновыми (в методе ВС им соответствуют спин-связанные (внутриорбитальные) или ковалентные комплексы).
В зависимости от силы поля лигандов заселение орбиталей электронами происходит по-разному. В слабом поле, в соответствии с правилом Хунда, сначала (t2g- и eg-орбитали) последовательно заселяются одним электроном, и лишь после этого начинается заселение вторыми электронами наиболее низких по энергии t2g-орбиталей (рис. 11.11). В сильном поле прежде всего полностью заселяются t2g-орбитали, а уже потом eg-орбитали.

Рис. 11.11. Заселение орбиталей электронами в сильном (а) и слабом (б) тетраэдрических кристаллических полях на примере d 5- и d 6-конфигураций
Соответствующие энергетические состояния характеризуют через заселенности t2g- и еg-орбиталей (например, t e25g g0).
При eg–t2g-расщеплении энергия eg-орбиталей (и их электронов) повышается на 6Dq, а энергия t2g-орбиталей понижается на 4Dq. В итоге энергия системы в целом уменьшается; этот энергетический выигрыш называют энергией стабилизации кристаллическим полем8 (ЭСКП, обозначается δ). Величина ЭСКП зависит от числа электронов на eg- и t2gорбиталях и во многом определяет главные свойства комплексного соединения.
Для октаэдрического поля ЭСКП (δ) рассчитывается по формуле:
δ = n(4Dq) – m(6Dq)
где n — число электронов на t2g-подуровне, m — число электронов на egподуровне. Например, ЭСКП для конфигурации t e23g g0:
δ = (4Dq) ⋅ 3 = 12Dq
а для конфигурации t e23g g2:
δ = (4Dq) ⋅ 3 – (6Dq) ⋅ 2 = 0
В случае сильного поля расчет аналогичен, однако необходимо учитывать иной порядок заполнения орбиталей, например для ЭСКП конфигу-
рации t e25g g0:
δ = (4Dq) ⋅ 5 = 20Dq
Таблица 11.2
Значения ЭСКП (Dq) для разных октаэдрических комплексов
Вопросы
11.10. Перечислите достоинства и недостатки метода валентных связей (ВС) (применительно к комплексным соединениям).
11.11. Определите диамагнитные и парамагнитные комплексы:
а) [Co(NH3)6]3; б) [TiF6]3–; в) [TiCl6]2–; г) [CuCl5]3–; д) [Cu(OH)6]4–;
е) [V(H2O)6]3; ж) [VCl4]–; з) [VF6]–; и) [Cu(CN)4]2–.
11.4.2. Теория кристаллического поля
Для предсказания строения комплексных соединений d-элементов хорошим дополнением к методу валентных связей оказалась теория кристаллического поля (КП). Основы этой теории были разработаны Бете в 1929 г. при рассмотрении эффекта замещения катиона натрия в решетке ионного кристалла типа NaCl. Бете показал, что при помещении свободного иона в электростатическое поле (так называемое кристаллическое поле), существующее в кристалле, происходит полное или частичное снятие вырождения энергетических подуровней иона, т. е. их расщепление.
Согласно теории кристаллического поля, вокруг положительно заряженного центрального иона упорядоченно располагаются точечные лиганды, которые заряжены отрицательно. Число этих точечных отрицательных зарядов определяет симметрию системы (комплекса). Реальный объем лигандов, а также их геометрическое и электронное строение во внимание не принимаются. Взаимодействие центрального атома с лигандами рассматривается с позиций квантовой механики. Энергия свободного (несвязанного) иона определяется кинетической энергией системы, энергией взаимодействия электрона с ядром, а также энергией межэлектронного и спин-орбитального взаимодействия6. При помещении иона в кристаллическое поле той или иной геометрии, которая зависит от симметрии системы в целом, на энергию системы дополнительно влияет потенциал V кристаллического поля. В теории кристаллического поля чаще рассматривают поля октаэдрической и тетраэдрической симметрии.
В поле сферической симметрии все орбитали d-подуровня свободных ионов переходных металлов вырождены (имеют одинаковую энергию). В электростатическом поле более низкой симметрии d-орбитали неэквивалентны по энергии (происходит расщепление подуровней, т. е. частичное снятие вырождения энергии). Расщепление подуровней в поле октаэдрической симметрии показано на рис. 11.10. Атомные dJ-орбитали (dx2−y2 и dz2 ) симметрии eg ближе всего подходят к орбиталям лигандов и подвер-

Рис. 11.10. Расщепление d-подуровня в кристаллическом поле октаэдрической симметрии гаются наиболее сильному воздействию их электростатического поля. Возникновение сил отталкивания приводит к увеличению энергии egорбиталей (они дестабилизируются). Три другие d-АО (dху, dxz, dyz) симметрии t2g, называемые dH, располагаются между орбиталями лигандов, поэтому их энергия понижается (орбитали стабилизируются).
Разность энергий eg- и t2g-состояний часто обозначают7 как 10Dq. Dq — это радиальный интеграл, который зависит от эффективного заряда и порядкового номера центрального иона Mn+, а также от расстояния металл—лиганд. В спектроскопии неорганических соединений величину Dq обычно называют основным параметром расщепления электронных конфигураций.
Характер расщепления определяется симметрией кристаллического поля и числом d-электронов иона переходного металла. Большое значение имеет также тип кристаллического поля, который зависит от природы лигандов. Чем сильнее поле лигандов, тем больше энергия расщепления. Обычно рассматривают два крайних случая — слабое и сильное кристаллические поля.
В слабом поле потенциал межэлектронного взаимодействия существенно больше потенциала кристаллического поля и, тем более, потенциала спин-орбитального взаимодействия. Координационные соединения с лигандами, создающими слабые кристаллические поля, называют высокоспиновыми (в методе ВС такие соединения называют спин-свободными (внешнеорбитальными) или ионными комплексами).
В сильном поле потенциал V заметно превышает потенциалы межэлектронного и спин-орбитального взаимодействий и поэтому подавляет их. Координационные соединения с лигандами, создающими сильные кристаллические поля, называют низкоспиновыми (в методе ВС им соответствуют спин-связанные (внутриорбитальные) или ковалентные комплексы).
В зависимости от силы поля лигандов заселение орбиталей электронами происходит по-разному. В слабом поле, в соответствии с правилом Хунда, сначала (t2g- и eg-орбитали) последовательно заселяются одним электроном, и лишь после этого начинается заселение вторыми электронами наиболее низких по энергии t2g-орбиталей (рис. 11.11). В сильном поле прежде всего полностью заселяются t2g-орбитали, а уже потом eg-орбитали.

Рис. 11.11. Заселение орбиталей электронами в сильном (а) и слабом (б) тетраэдрических кристаллических полях на примере d 5- и d 6-конфигураций
Соответствующие энергетические состояния характеризуют через заселенности t2g- и еg-орбиталей (например, t e25g g0).
При eg–t2g-расщеплении энергия eg-орбиталей (и их электронов) повышается на 6Dq, а энергия t2g-орбиталей понижается на 4Dq. В итоге энергия системы в целом уменьшается; этот энергетический выигрыш называют энергией стабилизации кристаллическим полем8 (ЭСКП, обозначается δ). Величина ЭСКП зависит от числа электронов на eg- и t2gорбиталях и во многом определяет главные свойства комплексного соединения.
Для октаэдрического поля ЭСКП (δ) рассчитывается по формуле:
δ = n(4Dq) – m(6Dq)
где n — число электронов на t2g-подуровне, m — число электронов на egподуровне. Например, ЭСКП для конфигурации t e23g g0:
δ = (4Dq) ⋅ 3 = 12Dq
а для конфигурации t e23g g2:
δ = (4Dq) ⋅ 3 – (6Dq) ⋅ 2 = 0
В случае сильного поля расчет аналогичен, однако необходимо учитывать иной порядок заполнения орбиталей, например для ЭСКП конфигу-
рации t e25g g0:
δ = (4Dq) ⋅ 5 = 20Dq
Таблица 11.2
Значения ЭСКП (Dq) для разных октаэдрических комплексов
Вопросы
11.10. Перечислите достоинства и недостатки метода валентных связей (ВС) (применительно к комплексным соединениям).
11.11. Определите диамагнитные и парамагнитные комплексы:
а) [Co(NH3)6]3; б) [TiF6]3–; в) [TiCl6]2–; г) [CuCl5]3–; д) [Cu(OH)6]4–;
е) [V(H2O)6]3; ж) [VCl4]–; з) [VF6]–; и) [Cu(CN)4]2–.
11.4.2. Теория кристаллического поля
Для предсказания строения комплексных соединений d-элементов хорошим дополнением к методу валентных связей оказалась теория кристаллического поля (КП). Основы этой теории были разработаны Бете в 1929 г. при рассмотрении эффекта замещения катиона натрия в решетке ионного кристалла типа NaCl. Бете показал, что при помещении свободного иона в электростатическое поле (так называемое кристаллическое поле), существующее в кристалле, происходит полное или частичное снятие вырождения энергетических подуровней иона, т. е. их расщепление.
Согласно теории кристаллического поля, вокруг положительно заряженного центрального иона упорядоченно располагаются точечные лиганды, которые заряжены отрицательно. Число этих точечных отрицательных зарядов определяет симметрию системы (комплекса). Реальный объем лигандов, а также их геометрическое и электронное строение во внимание не принимаются. Взаимодействие центрального атома с лигандами рассматривается с позиций квантовой механики. Энергия свободного (несвязанного) иона определяется кинетической энергией системы, энергией взаимодействия электрона с ядром, а также энергией межэлектронного и спин-орбитального взаимодействия6. При помещении иона в кристаллическое поле той или иной геометрии, которая зависит от симметрии системы в целом, на энергию системы дополнительно влияет потенциал V кристаллического поля. В теории кристаллического поля чаще рассматривают поля октаэдрической и тетраэдрической симметрии.
В поле сферической симметрии все орбитали d-подуровня свободных ионов переходных металлов вырождены (имеют одинаковую энергию). В электростатическом поле более низкой симметрии d-орбитали неэквивалентны по энергии (происходит расщепление подуровней, т. е. частичное снятие вырождения энергии). Расщепление подуровней в поле октаэдрической симметрии показано на рис. 11.10. Атомные dJ-орбитали (dx2−y2 и dz2 ) симметрии eg ближе всего подходят к орбиталям лигандов и подвер-

Рис. 11.10. Расщепление d-подуровня в кристаллическом поле октаэдрической симметрии гаются наиболее сильному воздействию их электростатического поля. Возникновение сил отталкивания приводит к увеличению энергии egорбиталей (они дестабилизируются). Три другие d-АО (dху, dxz, dyz) симметрии t2g, называемые dH, располагаются между орбиталями лигандов, поэтому их энергия понижается (орбитали стабилизируются).
Разность энергий eg- и t2g-состояний часто обозначают7 как 10Dq. Dq — это радиальный интеграл, который зависит от эффективного заряда и порядкового номера центрального иона Mn+, а также от расстояния металл—лиганд. В спектроскопии неорганических соединений величину Dq обычно называют основным параметром расщепления электронных конфигураций.
Характер расщепления определяется симметрией кристаллического поля и числом d-электронов иона переходного металла. Большое значение имеет также тип кристаллического поля, который зависит от природы лигандов. Чем сильнее поле лигандов, тем больше энергия расщепления. Обычно рассматривают два крайних случая — слабое и сильное кристаллические поля.
В слабом поле потенциал межэлектронного взаимодействия существенно больше потенциала кристаллического поля и, тем более, потенциала спин-орбитального взаимодействия. Координационные соединения с лигандами, создающими слабые кристаллические поля, называют высокоспиновыми (в методе ВС такие соединения называют спин-свободными (внешнеорбитальными) или ионными комплексами).
В сильном поле потенциал V заметно превышает потенциалы межэлектронного и спин-орбитального взаимодействий и поэтому подавляет их. Координационные соединения с лигандами, создающими сильные кристаллические поля, называют низкоспиновыми (в методе ВС им соответствуют спин-связанные (внутриорбитальные) или ковалентные комплексы).
В зависимости от силы поля лигандов заселение орбиталей электронами происходит по-разному. В слабом поле, в соответствии с правилом Хунда, сначала (t2g- и eg-орбитали) последовательно заселяются одним электроном, и лишь после этого начинается заселение вторыми электронами наиболее низких по энергии t2g-орбиталей (рис. 11.11). В сильном поле прежде всего полностью заселяются t2g-орбитали, а уже потом eg-орбитали.

Рис. 11.11. Заселение орбиталей электронами в сильном (а) и слабом (б) тетраэдрических кристаллических полях на примере d 5- и d 6-конфигураций
Соответствующие энергетические состояния характеризуют через заселенности t2g- и еg-орбиталей (например, t e25g g0).
При eg–t2g-расщеплении энергия eg-орбиталей (и их электронов) повышается на 6Dq, а энергия t2g-орбиталей понижается на 4Dq. В итоге энергия системы в целом уменьшается; этот энергетический выигрыш называют энергией стабилизации кристаллическим полем8 (ЭСКП, обозначается δ). Величина ЭСКП зависит от числа электронов на eg- и t2gорбиталях и во многом определяет главные свойства комплексного соединения.
Для октаэдрического поля ЭСКП (δ) рассчитывается по формуле:
δ = n(4Dq) – m(6Dq)
где n — число электронов на t2g-подуровне, m — число электронов на egподуровне. Например, ЭСКП для конфигурации t e23g g0:
δ = (4Dq) ⋅ 3 = 12Dq
а для конфигурации t e23g g2:
δ = (4Dq) ⋅ 3 – (6Dq) ⋅ 2 = 0
В случае сильного поля расчет аналогичен, однако необходимо учитывать иной порядок заполнения орбиталей, например для ЭСКП конфигу-
рации t e25g g0:
δ = (4Dq) ⋅ 5 = 20Dq
Таблица 11.2
Значения ЭСКП (Dq) для разных октаэдрических комплексов
| Электронная конфигурация | Примеры комплексообразователей | Слабое поле | Сильное поле |
| d 0 | Ca2, Sc3 | 0 | 0 |
| d1 | Ti3, U4 | 4 | 4 |
| d2 | Ti2, V3 | 8 | 8 |
| d 3 | V2, Cr3 | 12 | 12 |
| d 4 | Cr2, Mn3 | 6 | 16 |
| d 5 | Mn2, Fe3, Os3 | 0 | 20 |
| d 6 | Fe2, Co3, Ir3 | 4 | 24 |
| d 7 | Co2, Ni3, Rh2 | 8 | 18 |
| d 8 | Ni2, Pd2, Pt2, Au3 | 12 | 12 |
| d 9 | Cu2, Ag2 | 6 | 6 |
| d10 | Cu, Zn2, Cd2, Ag, Hg2, Ga3 | 0 | 0 |
Для электронных конфигураций d 0 и d10, а также в случае слабого поля лигандов, для конфигурации d 5, ЭСКП равна нулю (табл. 11.2).
При точном расчете ЭСКП нужно также учитывать, что для заселения одной и той же орбитали двумя электронами с противоположными спинами необходимо затратить энергию на преодоление отталкивания электронов (табл. 11.3). Эту величину называют энергией спин-спаривания (Р ).
Таблица 11.3
Энергия спин-спаривания и энергия расщепления для некоторых октаэдрических комплексов d-элементов
| Комплексообразователь | Энергия спинспаривания, кДж / моль | | Энергия расщепления поле лигандов, кДж / моль | м | |
| F– | Н2O | NH3 | CN– | ||
| Сr4 (3d2) | — | 246,0 | — | — | — |
| Сr3 (3d3) | — | 166,9 | 194,9 | 241,2 | 298,2 |
| Mn2 (3d 5) | 304 | 217,1 | 209,4 | — | 306,8 |
| Fе2 (3d 6) | 209 | — | 130,2 | — | 359,9 |
| Fе3 (3d 5) | 357 | 149,6 | 156,3 | — | 390,8 |
| Со2 (3d7) | 304 | — | 103,2 | 113,9 | — |
| Со3 (3d 6) | 250 | 146,6 | 232,5 | 255,7 | 359,9 |
| Rh3 (4d 6) | — | — | 303,9 | 381,1 | 501,7 |
Порядок заселения d-орбиталей определяет число неспаренных электронов и, следовательно, магнитные свойства комплексных соединений. Для комплексов 3