Файл: Умноженной на множитель в форме показательной функции W.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 446
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
xp(n) и Xp(k) полностью определяются одним периодом xp(n)
коэффициенты ДПФ последовательности конечной длины равны значениям z-преобразования этой же последовательности в N точках, равномерно распределенных по единичной окружности. Еще более важный вывод состоит в том, что коэффициенты ДПФ последовательности конечной длины однозначно представляют саму последовательность, т.к. по ним можно точно восстановить исходную последовательность, используя ОДПФ. Итак, хотя ДПФ и ОДПФ вводятся для периодических последовательностей, важно, что через них можно представлять последовательности конечной длины.
Свойства:
Если xp(n) и yp(n) – периодические последовательности (с периодом в N отсчетов каждая), а Xp(k) и Yp(k) – их ДПФ, то дискретное преобразование Фурье последовательности xp(n)+ yp(n) равно Xp(k) + Yp(k). Это положение справедливо и для последовательностей конечной длины.
2. Свойство симметрии. Если периодическая последовательность xp(n) с периодом в N отсчетов является действительной, то ее ДПФ Xp(k) удовлетворяет следующим условиям симметрии
Re[Xp(k)]=Re[Xp(N-k)]
Im[Xp(k)]=-Im[Xp(N-k)]
| Xp(k)|=| Xp(N-k)|
arg Xp(k)=-arg Xp(N-k)
Аналогичные равенства справедливы и для конечной последовательности x(n), имеющей N-точечное ДПФ X(k).
3.Сдвиг по времени:
циклический сдвиг сигнала на отсчетов приводит к повороту фазового спектра, в то время как амплитудный спектр не меняется.
4.Сдвиг по частоте:
Пусть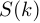 — ДПФ сигнала
— ДПФ сигнала 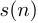 .
.
Произведем циклический сдвиг спектра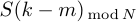 и рассмотрим ОДПФ, тогда:
и рассмотрим ОДПФ, тогда:
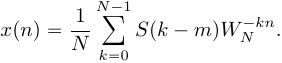
(19)
Введем замену переменной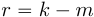 , тогда
, тогда 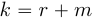 и (19) принимает вид:
и (19) принимает вид:
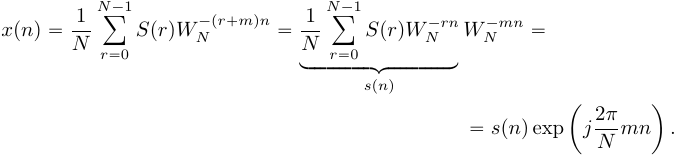
(20)
Таким образом, циклический частотный сдвиг ДПФ осуществляется умножением сигнала на комплексную экспоненту.
Важно отметить, что после умножения на комплексную экспоненту вещественного сигнала, результирующий сигнал будет комплексным, а его спектр перестанет быть симметричным.
5.Произведение последовательностей
Пусть сигнал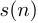 равен произведению сигналов
равен произведению сигналов 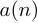 и
и 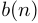 , т.е.
, т.е. 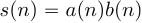
, причем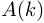 и
и 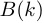 — ДПФ сигналов
— ДПФ сигналов  и
и  соответственно.
соответственно.
Тогда ДПФ сигнала равно:
равно:
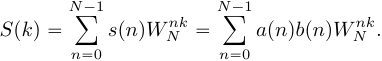
(16)
Подставим в (16) в виде ОДПФ от спектра
в виде ОДПФ от спектра 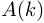 :
:
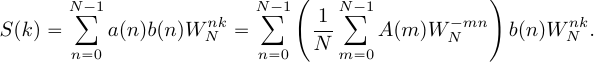
(17)
Поменяем местами операции суммирования в выражении (17) и получим:
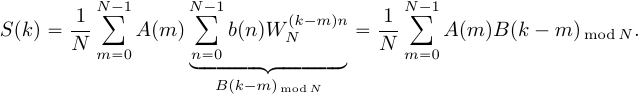
(18)
Таким образом, ДПФ произведения сигналов представляет собой циклическую свертку ДПФ этих сигналов. Цикличность свертки также объясняется периодичностью спектров ДПФ. Именно по этому был добавлен индекс взятия сдвинутого спектрального отсчета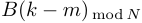 по модулю . При
по модулю . При 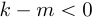 мы должны взять спектральный отсчет c отрицательным индексом, который соответствует отсчету
мы должны взять спектральный отсчет c отрицательным индексом, который соответствует отсчету 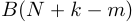 .
.
6.Циклическая свертка
Пусть сигнал есть результат циклической свертки сигналов
есть результат циклической свертки сигналов  и
и 
:
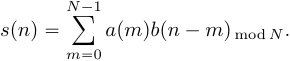
(13)
Рассчитаем ДПФ сигнала :
:
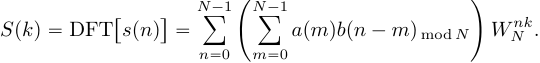
(14)
Поменяем местами операции суммирования:
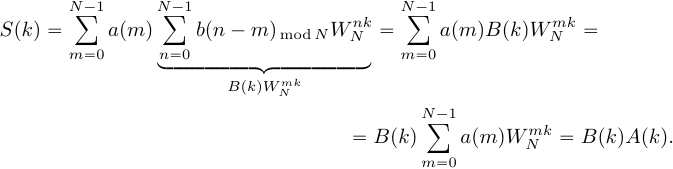
(15)
При выводе выражения (15) было использовано свойство циклического временного сдвига.
Таким образом, ДПФ циклической свертки двух сигналов равен произведению ДПФ этих сигналов.
Это свойство позволяет использовать алгоритмы быстрого преобразования Фурье для вычисления сверток сигналов.
Разделение исходной последовательности прореживанием по времени
Прореживание по времени заключается в разделении исходной последовательности ,
,  , на две последовательности половинной длительности
, на две последовательности половинной длительности 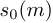 и
и 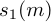 ,
,  , таким образом, что
, таким образом, что 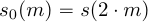 , а
, а 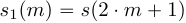 .
.
Последовательность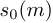 содержит отсчеты с четными индексами, а
содержит отсчеты с четными индексами, а
 — с нечетными.
— с нечетными.
Прореживание по времени для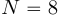 наглядно представлено на рисунке 1.
наглядно представлено на рисунке 1.
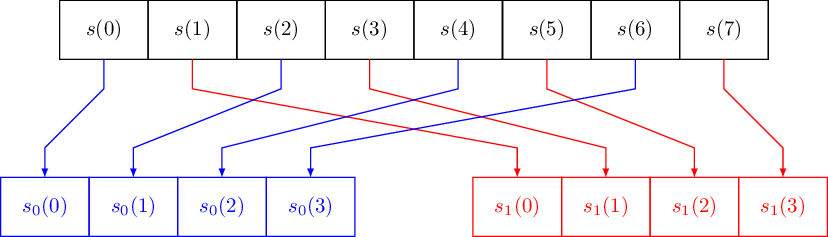
Рисунок 1. Прореживание по времени для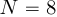
Процедура объединения
ДПФ, окончательно можно записать процедуру объединения как:
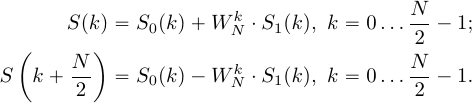
(12)
Граф <<бабочка>>
Выражение (12) объединяет два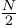 -точечных ДПФ
-точечных ДПФ 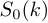 и
и 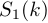 ,
,  , прореженных сигналов половинной длительности
, прореженных сигналов половинной длительности 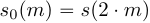 и
и 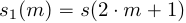 ,
,  , в результирующее -точечное ДПФ
, в результирующее -точечное ДПФ  ,
,  , исходного сигнала.
, исходного сигнала.
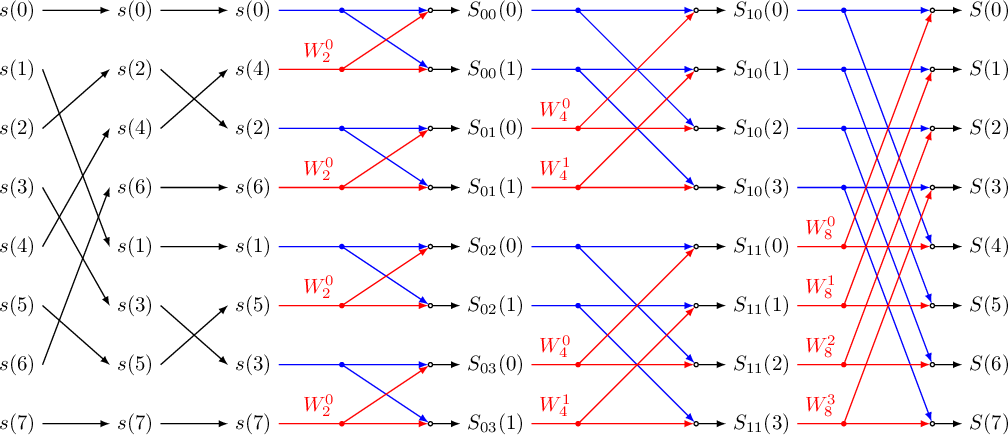
Рисунок 4. Граф алгоритма БПФ с прореживанием по времени для
На первом этапе отсчеты входного сигнала переставляются местами и исходная последовательность делится на «четную» и «нечетную» последовательности. Потом «четная» и «нечетная» последовательности в свою очередь делятся на «четную» и «нечетную» последовательности.
коэффициенты ДПФ последовательности конечной длины равны значениям z-преобразования этой же последовательности в N точках, равномерно распределенных по единичной окружности. Еще более важный вывод состоит в том, что коэффициенты ДПФ последовательности конечной длины однозначно представляют саму последовательность, т.к. по ним можно точно восстановить исходную последовательность, используя ОДПФ. Итак, хотя ДПФ и ОДПФ вводятся для периодических последовательностей, важно, что через них можно представлять последовательности конечной длины.
Свойства:
-
Линейность
Если xp(n) и yp(n) – периодические последовательности (с периодом в N отсчетов каждая), а Xp(k) и Yp(k) – их ДПФ, то дискретное преобразование Фурье последовательности xp(n)+ yp(n) равно Xp(k) + Yp(k). Это положение справедливо и для последовательностей конечной длины.
2. Свойство симметрии. Если периодическая последовательность xp(n) с периодом в N отсчетов является действительной, то ее ДПФ Xp(k) удовлетворяет следующим условиям симметрии
Re[Xp(k)]=Re[Xp(N-k)]
Im[Xp(k)]=-Im[Xp(N-k)]
| Xp(k)|=| Xp(N-k)|
arg Xp(k)=-arg Xp(N-k)
Аналогичные равенства справедливы и для конечной последовательности x(n), имеющей N-точечное ДПФ X(k).
3.Сдвиг по времени:
циклический сдвиг сигнала на отсчетов приводит к повороту фазового спектра, в то время как амплитудный спектр не меняется.
4.Сдвиг по частоте:
Пусть
Произведем циклический сдвиг спектра
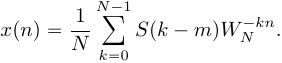
(19)
Введем замену переменной
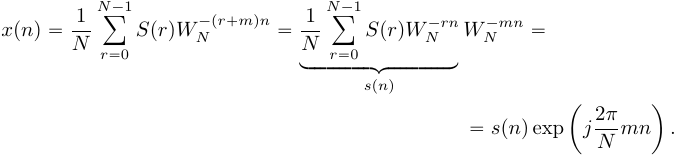
(20)
Таким образом, циклический частотный сдвиг ДПФ осуществляется умножением сигнала на комплексную экспоненту.
Важно отметить, что после умножения на комплексную экспоненту вещественного сигнала, результирующий сигнал будет комплексным, а его спектр перестанет быть симметричным.
5.Произведение последовательностей
Пусть сигнал
, причем
Тогда ДПФ сигнала
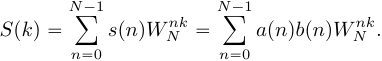
(16)
Подставим в (16)
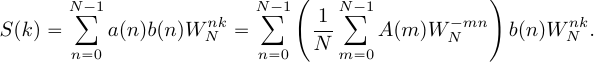
(17)
Поменяем местами операции суммирования в выражении (17) и получим:
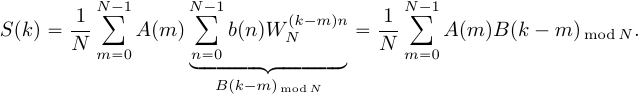
(18)
Таким образом, ДПФ произведения сигналов представляет собой циклическую свертку ДПФ этих сигналов. Цикличность свертки также объясняется периодичностью спектров ДПФ. Именно по этому был добавлен индекс взятия сдвинутого спектрального отсчета
6.Циклическая свертка
Пусть сигнал
:
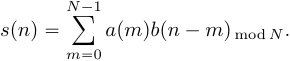
(13)
Рассчитаем ДПФ сигнала
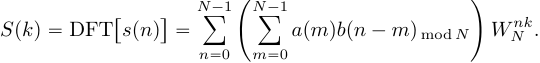
(14)
Поменяем местами операции суммирования:
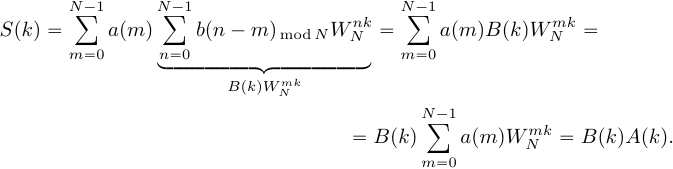
(15)
При выводе выражения (15) было использовано свойство циклического временного сдвига.
Таким образом, ДПФ циклической свертки двух сигналов равен произведению ДПФ этих сигналов.
Это свойство позволяет использовать алгоритмы быстрого преобразования Фурье для вычисления сверток сигналов.
- Быстрое преобразование Фурье (БПФ) с прореживанием по времени для размера блока N = 2r. Понятие о поворачивающем множителе. Понятие о графе «бабочка» для БПФ с прореживанием по времени, алгоритм его работы. Пример структуры модуля БПФ на основе 8-точечного БПФ. Понятие о бит-реверсной перестановке элементов последовательности.
Разделение исходной последовательности прореживанием по времени
Прореживание по времени заключается в разделении исходной последовательности
Последовательность
Прореживание по времени для

Рисунок 1. Прореживание по времени для
Процедура объединения
ДПФ, окончательно можно записать процедуру объединения как:
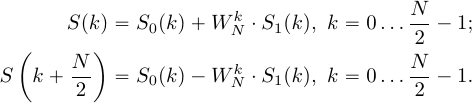
(12)
Граф <<бабочка>>
Выражение (12) объединяет два

Рисунок 4. Граф алгоритма БПФ с прореживанием по времени для
На первом этапе отсчеты входного сигнала переставляются местами и исходная последовательность делится на «четную» и «нечетную» последовательности. Потом «четная» и «нечетная» последовательности в свою очередь делятся на «четную» и «нечетную» последовательности.