Файл: Курсовая работа применение дифференциальных уравнений к решению экономических задач Обучающийся 4 курса.docx
Добавлен: 11.01.2024
Просмотров: 275
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
2.Задачи экономики, приводящиеся к дифференциальным уравнениям
2.1.Рост общественного благосостояния (модель Золотаса)
2.2.Модель экономического роста (Модель Солоу)
2.3.Динамика рыночной цены (модель Самуэльсона)
2.6.Интенсивность выпуска продукции
2.7.Естественный рост выпуска продукции
2.9.Анализ производительности труда
2.10. Модель рынка с прогнозируемыми ценами.
,то мы можем сказать, что из (9) следует
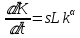 (10).
(10).
Затем так как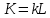 , то исходя из
, то исходя из 
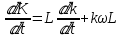 (11).
(11).
Если мы приравниваем правые части ДУ (10) и (11) и делим их на , то приходим к уравнению Бернулли [1]:
, то приходим к уравнению Бернулли [1]:
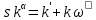 (12).
(12).
Вводим новую искомую функцию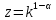 и приводим (12) к линейному неоднородному ДУ [7] первого порядка относительно какой-то новой функции:
и приводим (12) к линейному неоднородному ДУ [7] первого порядка относительно какой-то новой функции:
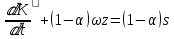 (13).
(13).
Общее решение ДУ можем записать в следующем виде:
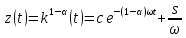 (14).
(14).
Если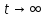 , то
, то 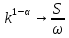 , или
, или 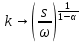 . Тогда, отношение
. Тогда, отношение 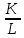 ( данное отношение всегда будем рассматривать в качестве основной характеристики экономического роста) будет стремиться к какой-то постоянной величине, которая повышается с увеличением доли сбережений
( данное отношение всегда будем рассматривать в качестве основной характеристики экономического роста) будет стремиться к какой-то постоянной величине, которая повышается с увеличением доли сбережений 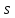 в доходе и убывает с увеличением темпа роста трудовых ресурсов
в доходе и убывает с увеличением темпа роста трудовых ресурсов 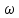 . На данном этапе нужно обязательно выделить, что до этого величины
. На данном этапе нужно обязательно выделить, что до этого величины 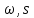 считались постоянными (т.е. не зависящими от времени), а
считались постоянными (т.е. не зависящими от времени), а 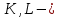 функциями от времени. Следовательно,
функциями от времени. Следовательно, 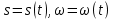 . Тогда все размышления, которые приводят к ДУ (13), будут сохраняться, однако решением будем считать
. Тогда все размышления, которые приводят к ДУ (13), будут сохраняться, однако решением будем считать
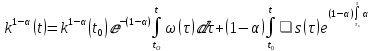 (15).
(15).
При постоянных доли сбережений в доходе и темпа роста L формула (15) обязательно должна совпадать с (14). Учитывая, что из (14) следует
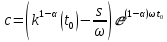
,
тогда нетрудно убедиться в указанном совпадении.
Изучая модель Самуэльсона, можно выделить то, что она подразумевает только рынок благ, и поэтому уровень цен и ставка процента планируются неизменными, а тогда можно сделать вывод, что объем предложения благ абсолютно точно эластичен. [8]
В этой модели рассмотрим моделирования и потребления взаимосвязи изменения цены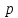 и неудовлетворенного спроса:
и неудовлетворенного спроса: 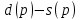 , где
, где
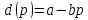 ,
, 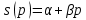 это соответственно спрос и предложение, которые линейно зависят от цены.
это соответственно спрос и предложение, которые линейно зависят от цены.
Математическая модель задачи. Соответственно модели Самуэльсона, скорость изменения цены прямо пропорциональна неудовлетворенному спросу с некоторым коэффициентом пропорциональности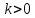 , то есть
, то есть
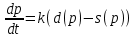 (16).
(16).
С учетом точного вида функцией спроса и предложения данное ДУ будет принимать вид
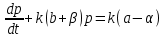 (17).
(17).
Решение задачи. Заметно ясно, что ДУ (17) – это линейное уравнение с постоянными коэффициентами.
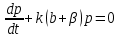 (18).
(18).
Общее решение соответствующего однородного уравнения запишем в виде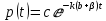 . Тогда частное решение неоднородного уравнения найдем с помощью метода неопределенных коэффициентов и получим постоянную
. Тогда частное решение неоднородного уравнения найдем с помощью метода неопределенных коэффициентов и получим постоянную 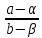 , которая будет являться равновесной ценой, то есть ценой, когда спрос равен предложению.
, которая будет являться равновесной ценой, то есть ценой, когда спрос равен предложению.
Таким образом, получаем
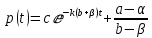 (19).
(19).
Из полученного решения можно заметить, что если коэффициенты будут положительными, то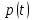 стремится с течением времени к своей равновесной цене.
стремится с течением времени к своей равновесной цене.
Представим, что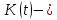 это величина фондов в стоимостном выражении, тогда через
это величина фондов в стоимостном выражении, тогда через 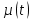 запишем коэффициент выбытия фондов,
запишем коэффициент выбытия фондов, 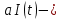 инвестиции. Убыток будет вести к редуцированию фондов за год на величину
инвестиции. Убыток будет вести к редуцированию фондов за год на величину 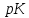 , а если мы будем считать, что выход фондов происходит более менее плавно, то за время
, а если мы будем считать, что выход фондов происходит более менее плавно, то за время 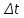 фонды уменьшатся на
фонды уменьшатся на 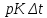 . [4]
. [4]
Однако равным образом инвестиции приводят к расширению фондов на некоторую величину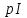 . Тогда можем сказать, что за время
. Тогда можем сказать, что за время 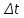 при равномерном вложении инвестиции будут давать прибавление фондов на величину
при равномерном вложении инвестиции будут давать прибавление фондов на величину 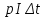 .
.
Математическая модель задачи. Если мы учитываем все предположения, то
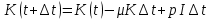 (20).
(20).
Разделим обе части на величину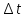 , мы получим
, мы получим
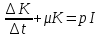 (21).
(21).
Если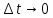 , то получаем ДУ:
, то получаем ДУ:
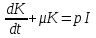 (22).
(22).
Решение задачи. Полученное уравнение (22) представляет собой ЛНДУ первого порядка. Для того чтобы решить данное уравнение достаточно воспользоваться методом вариации произвольной постоянной:
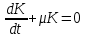 (23).
(23).
Уравнение (23) будет являться ДУ с разделяющимися переменными:
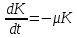 ,
,
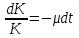 ,
,
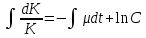 ,
,
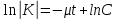 (24).
(24).
Равенство (24) является интегралом линейного однородного ДУ. Получим общее решение в виде
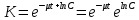 ,
,
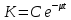
(25).
Для того чтобы найти решение уравнения заменим постоянную С некоторой неизвестной функцией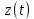 :
:
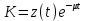 (26).
(26).
Продифференцируем функцию и получим:
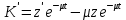 (27).
(27).
Далее подставляем в (22) вместо и
и 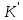 , то, что нашли ранее и получим:
, то, что нашли ранее и получим:
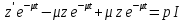 ,
,
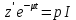 ,
,
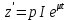 (28).
(28).
Уравнение (28) – простейшее ДУ и его решение можем записать в виде:
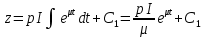 (29).
(29).
Следующим шагом подставляем в уравнение (26) найденное выражение:
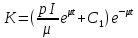 .
.
Тогда искомая величина фондов будет выражаться зависимостью
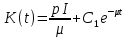 (30).
(30).
Математическая модель задачи. Для того, чтобы узнать изменение числа потребителей с помощью данной модели, используют следующее дифференциальное уравнение:
с помощью данной модели, используют следующее дифференциальное уравнение:
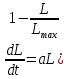 ), (31)
), (31)
где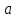 – постоянна и строго больше нуля, а
– постоянна и строго больше нуля, а 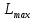 является верхним пределом потребителей.
является верхним пределом потребителей.
Решение задачи. Тогда можно заметить, что решение дифференциального уравнения найдется по формуле:
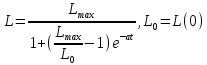 (32).
(32).
Здесь мы будем наблюдать торможение роста числа потребителей некоторой фирмы с течением времени.[3]
Пусть интенсивность выпуска некоторой продукции предприятием или фирмой можно определить функцией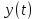 . Мы можем сказать, что вследствие быстрого роста выпуска продукции будет со временем насыщаться рынок, тогда из-за этого цена товара
. Мы можем сказать, что вследствие быстрого роста выпуска продукции будет со временем насыщаться рынок, тогда из-за этого цена товара
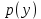 будет снижаться и зависимость будет линейной:
будет снижаться и зависимость будет линейной:
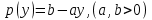 (33).
(33).
Тогда представим, что стремительность роста интенсивности выпуска продукции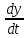 будет возрастающей функцией дохода:
будет возрастающей функцией дохода:
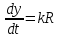 ,
,
где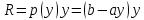 считаем доходом от продажи выпуска
считаем доходом от продажи выпуска 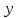 продукции по цене
продукции по цене 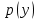 .
.
Математическая модель задачи. Уравнение представленного процесса является ДУ первого порядка с разделяющимися переменными:
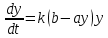 (34).
(34).
Решение задачи. Для поиска решения данного уравнения, нам нужно разделить переменные:
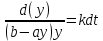 (35)
(35)
Интегрируем:
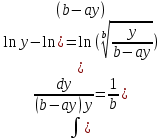 (36),
(36),
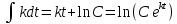 ,
,
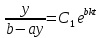 , (
, (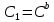 ) (37).
) (37).
Решение уравнения (34) запишем в виде:
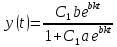 (38).
(38).
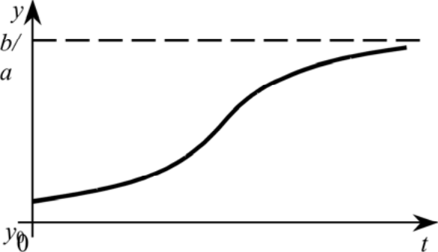
Рис 2. Логистическая кривая
Произвольную постоянную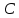 можно вычислить, если известно значение
можно вычислить, если известно значение 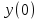 .
.
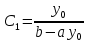 .
.
Решение уравнения (38) представляет уравнение логистической кривой. В данном примере логистическая кривая указывает, что с увеличением времени происходит насыщение рынка. [6]
В данном случае будем разбирать модель естественного роста выпуска какой-то продукции, которая продается на рынке по некоторой фиксированной цене
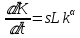 (10).
(10).Затем так как
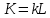 , то исходя из
, то исходя из 
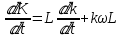 (11).
(11).Если мы приравниваем правые части ДУ (10) и (11) и делим их на
 , то приходим к уравнению Бернулли [1]:
, то приходим к уравнению Бернулли [1]: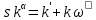 (12).
(12).Вводим новую искомую функцию
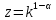 и приводим (12) к линейному неоднородному ДУ [7] первого порядка относительно какой-то новой функции:
и приводим (12) к линейному неоднородному ДУ [7] первого порядка относительно какой-то новой функции: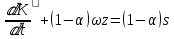 (13).
(13).Общее решение ДУ можем записать в следующем виде:
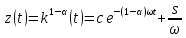 (14).
(14).Если
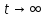 , то
, то 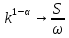 , или
, или 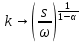 . Тогда, отношение
. Тогда, отношение 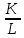 ( данное отношение всегда будем рассматривать в качестве основной характеристики экономического роста) будет стремиться к какой-то постоянной величине, которая повышается с увеличением доли сбережений
( данное отношение всегда будем рассматривать в качестве основной характеристики экономического роста) будет стремиться к какой-то постоянной величине, которая повышается с увеличением доли сбережений 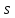 в доходе и убывает с увеличением темпа роста трудовых ресурсов
в доходе и убывает с увеличением темпа роста трудовых ресурсов 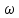 . На данном этапе нужно обязательно выделить, что до этого величины
. На данном этапе нужно обязательно выделить, что до этого величины 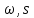 считались постоянными (т.е. не зависящими от времени), а
считались постоянными (т.е. не зависящими от времени), а 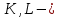 функциями от времени. Следовательно,
функциями от времени. Следовательно, 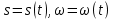 . Тогда все размышления, которые приводят к ДУ (13), будут сохраняться, однако решением будем считать
. Тогда все размышления, которые приводят к ДУ (13), будут сохраняться, однако решением будем считать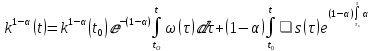 (15).
(15).При постоянных доли сбережений в доходе и темпа роста L формула (15) обязательно должна совпадать с (14). Учитывая, что из (14) следует
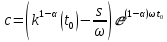
,
тогда нетрудно убедиться в указанном совпадении.
2.3.Динамика рыночной цены (модель Самуэльсона)
Изучая модель Самуэльсона, можно выделить то, что она подразумевает только рынок благ, и поэтому уровень цен и ставка процента планируются неизменными, а тогда можно сделать вывод, что объем предложения благ абсолютно точно эластичен. [8]
В этой модели рассмотрим моделирования и потребления взаимосвязи изменения цены
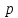 и неудовлетворенного спроса:
и неудовлетворенного спроса: 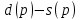 , где
, где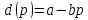 ,
, 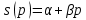 это соответственно спрос и предложение, которые линейно зависят от цены.
это соответственно спрос и предложение, которые линейно зависят от цены.Математическая модель задачи. Соответственно модели Самуэльсона, скорость изменения цены прямо пропорциональна неудовлетворенному спросу с некоторым коэффициентом пропорциональности
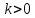 , то есть
, то есть 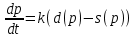 (16).
(16).С учетом точного вида функцией спроса и предложения данное ДУ будет принимать вид
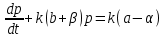 (17).
(17).Решение задачи. Заметно ясно, что ДУ (17) – это линейное уравнение с постоянными коэффициентами.
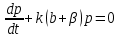 (18).
(18).Общее решение соответствующего однородного уравнения запишем в виде
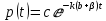 . Тогда частное решение неоднородного уравнения найдем с помощью метода неопределенных коэффициентов и получим постоянную
. Тогда частное решение неоднородного уравнения найдем с помощью метода неопределенных коэффициентов и получим постоянную 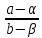 , которая будет являться равновесной ценой, то есть ценой, когда спрос равен предложению.
, которая будет являться равновесной ценой, то есть ценой, когда спрос равен предложению. Таким образом, получаем
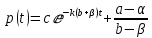 (19).
(19).Из полученного решения можно заметить, что если коэффициенты будут положительными, то
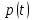 стремится с течением времени к своей равновесной цене.
стремится с течением времени к своей равновесной цене.2.4.Движение фондов
Представим, что
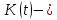 это величина фондов в стоимостном выражении, тогда через
это величина фондов в стоимостном выражении, тогда через 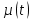 запишем коэффициент выбытия фондов,
запишем коэффициент выбытия фондов, 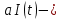 инвестиции. Убыток будет вести к редуцированию фондов за год на величину
инвестиции. Убыток будет вести к редуцированию фондов за год на величину 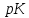 , а если мы будем считать, что выход фондов происходит более менее плавно, то за время
, а если мы будем считать, что выход фондов происходит более менее плавно, то за время 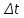 фонды уменьшатся на
фонды уменьшатся на 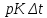 . [4]
. [4]Однако равным образом инвестиции приводят к расширению фондов на некоторую величину
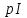 . Тогда можем сказать, что за время
. Тогда можем сказать, что за время 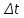 при равномерном вложении инвестиции будут давать прибавление фондов на величину
при равномерном вложении инвестиции будут давать прибавление фондов на величину 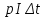 .
.Математическая модель задачи. Если мы учитываем все предположения, то
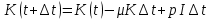 (20).
(20).Разделим обе части на величину
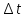 , мы получим
, мы получим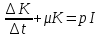 (21).
(21).Если
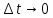 , то получаем ДУ:
, то получаем ДУ: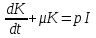 (22).
(22).Решение задачи. Полученное уравнение (22) представляет собой ЛНДУ первого порядка. Для того чтобы решить данное уравнение достаточно воспользоваться методом вариации произвольной постоянной:
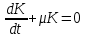 (23).
(23).Уравнение (23) будет являться ДУ с разделяющимися переменными:
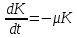 ,
,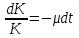 ,
,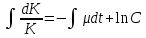 ,
,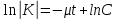 (24).
(24).Равенство (24) является интегралом линейного однородного ДУ. Получим общее решение в виде
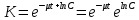 ,
,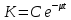
(25).
Для того чтобы найти решение уравнения заменим постоянную С некоторой неизвестной функцией
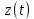 :
: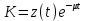 (26).
(26).Продифференцируем функцию и получим:
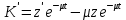 (27).
(27).Далее подставляем в (22) вместо
 и
и 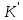 , то, что нашли ранее и получим:
, то, что нашли ранее и получим: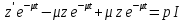 ,
,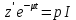 ,
,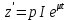 (28).
(28).Уравнение (28) – простейшее ДУ и его решение можем записать в виде:
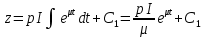 (29).
(29).Следующим шагом подставляем в уравнение (26) найденное выражение:
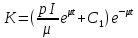 .
.Тогда искомая величина фондов будет выражаться зависимостью
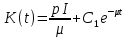 (30).
(30).2.5.Динамика потребителей
Математическая модель задачи. Для того, чтобы узнать изменение числа потребителей
 с помощью данной модели, используют следующее дифференциальное уравнение:
с помощью данной модели, используют следующее дифференциальное уравнение: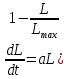 ), (31)
), (31)где
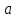 – постоянна и строго больше нуля, а
– постоянна и строго больше нуля, а 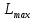 является верхним пределом потребителей.
является верхним пределом потребителей. Решение задачи. Тогда можно заметить, что решение дифференциального уравнения найдется по формуле:
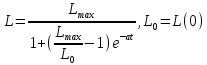 (32).
(32).Здесь мы будем наблюдать торможение роста числа потребителей некоторой фирмы с течением времени.[3]
2.6.Интенсивность выпуска продукции
Пусть интенсивность выпуска некоторой продукции предприятием или фирмой можно определить функцией
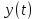 . Мы можем сказать, что вследствие быстрого роста выпуска продукции будет со временем насыщаться рынок, тогда из-за этого цена товара
. Мы можем сказать, что вследствие быстрого роста выпуска продукции будет со временем насыщаться рынок, тогда из-за этого цена товара
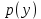 будет снижаться и зависимость будет линейной:
будет снижаться и зависимость будет линейной: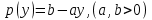 (33).
(33).Тогда представим, что стремительность роста интенсивности выпуска продукции
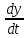 будет возрастающей функцией дохода:
будет возрастающей функцией дохода: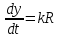 ,
,где
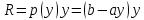 считаем доходом от продажи выпуска
считаем доходом от продажи выпуска 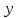 продукции по цене
продукции по цене 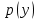 .
.Математическая модель задачи. Уравнение представленного процесса является ДУ первого порядка с разделяющимися переменными:
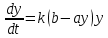 (34).
(34).Решение задачи. Для поиска решения данного уравнения, нам нужно разделить переменные:
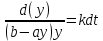 (35)
(35)Интегрируем:
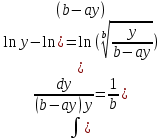 (36),
(36),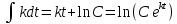 ,
,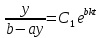 , (
, (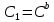 ) (37).
) (37).Решение уравнения (34) запишем в виде:
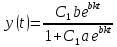 (38).
(38).
Рис 2. Логистическая кривая
Произвольную постоянную
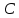 можно вычислить, если известно значение
можно вычислить, если известно значение 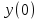 .
.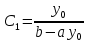 .
.Решение уравнения (38) представляет уравнение логистической кривой. В данном примере логистическая кривая указывает, что с увеличением времени происходит насыщение рынка. [6]
2.7.Естественный рост выпуска продукции
В данном случае будем разбирать модель естественного роста выпуска какой-то продукции, которая продается на рынке по некоторой фиксированной цене
