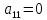Файл: Курсовая работа применение дифференциальных уравнений к решению экономических задач Обучающийся 4 курса.docx
Добавлен: 11.01.2024
Просмотров: 272
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
2.Задачи экономики, приводящиеся к дифференциальным уравнениям
2.1.Рост общественного благосостояния (модель Золотаса)
2.2.Модель экономического роста (Модель Солоу)
2.3.Динамика рыночной цены (модель Самуэльсона)
2.6.Интенсивность выпуска продукции
2.7.Естественный рост выпуска продукции
2.9.Анализ производительности труда
2.10. Модель рынка с прогнозируемыми ценами.
. Представим, что q(t) – это количество продукции, которая осуществляется на определенный момент времени 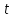 . Тогда можем точно сказать, что на данный момент времени получен доход –
. Тогда можем точно сказать, что на данный момент времени получен доход – 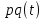 , часть которого будет тратиться на инвестиции в изготовление выпускаемой продукции, то есть
, часть которого будет тратиться на инвестиции в изготовление выпускаемой продукции, то есть 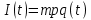 , при этом
, при этом 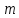 - норма инвестиции,
- норма инвестиции, 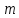 постоянна
постоянна 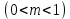 .
.
Математическая модель задачи. Вследствие всех наших предположений о том, что рынок некрепкий и продукция осуществляется там полностью, мы можем отметить, что если увеличивается количество производства, то в результате получается возрастание дохода. Однако часть его будет снова тратиться для расширения выпуска товара, что в конечном итоге должно привести к увеличению стремительности выпуска. Последнее будет пропорционально увеличению инвестиций:
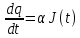 (39).
(39).
Получаем ДУ:
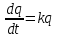 , (40).
, (40).
где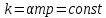 .
.
Решение задачи. Здесь представленное уравнение (40) снова является ДУ с разделяющимися прямыми. Решим уравнение и получим ответ в виде:
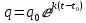 (41).
(41).
Выражение (41) будет определять модель естественного роста выпуска продукции. [6]
Математическая модель задачи. Для представления ситуации сразу рассмотрим пример. Пусть фирма реализует какой-то товар, о котором в определенный момент времени из числа потенциальных потребителей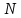 знают только
знают только  число потребителей. Можем выдвинуть предположение о том, что для увеличения продажи их продукции была дана некоторая реклама на вывесках, билбордах, радио, телевидении или в социальных сетях. Далее будем ориентироваться на то, что информация о продукции распространяется среди покупателей только «сарафанным радио», то есть только при общении покупателей друг с другом. С достаточно большой долей подлинности можно уверенно отметить, что после рекламных объявлений стремительность изменения числа о продукции пропорциональна и числу знающих, и незнающих о продукции. Далее будем стараться отсчитывать время с момента выхода рекламных объявлений, когда о товаре узнало
число потребителей. Можем выдвинуть предположение о том, что для увеличения продажи их продукции была дана некоторая реклама на вывесках, билбордах, радио, телевидении или в социальных сетях. Далее будем ориентироваться на то, что информация о продукции распространяется среди покупателей только «сарафанным радио», то есть только при общении покупателей друг с другом. С достаточно большой долей подлинности можно уверенно отметить, что после рекламных объявлений стремительность изменения числа о продукции пропорциональна и числу знающих, и незнающих о продукции. Далее будем стараться отсчитывать время с момента выхода рекламных объявлений, когда о товаре узнало
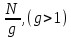 количество человек, то есть
количество человек, то есть 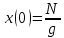 .
.
Решение задачи. Вышеописанный процесс можно опишем некоторым ДУ:
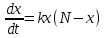 , (42)
, (42)
где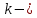 снова коэффициент пропорциональности.
снова коэффициент пропорциональности.
Проинтегрируем уравнение (42) и придем к некоторой логистической кривой:
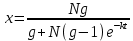 (43).
(43).
Выражение, которое мы получили, позволяет нам вычислить количество людей, которые узнали о товаре, в абсолютно любой момент времени строго больший нуля. [4]
Представим, что на некотором предприятии рост трансформации производительности труда в определенный момент времени задается некоторым отношением:
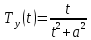 (44).
(44).
Если в момент времени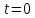 производительность труда равна
производительность труда равна 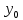 , то мы можем абсолютно точно найти закон изменения производительности труда.
, то мы можем абсолютно точно найти закон изменения производительности труда.
Математическая модель задачи. Под ростом будем понимать:
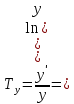 (45).
(45).
Далее по условию задачи получаем некоторое дифференциальное уравнение:
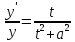 (46).
(46).
Решение задачи. Представим в виде дифференциалов:
в виде дифференциалов:
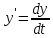 (47).
(47).
Приходим снова к ДУ с разделяющимися переменными:
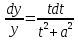 (48).
(48).
Интегрируем полученное уравнение (48) и получим его решение в виде:
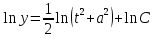 ,
,
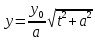 [6].
[6].
В данном случае постараемся достаточно достоверно изучить модель рынка с прогнозируемыми ценами. В обыкновенных моделях рынка, спрос и предложение обычно рассчитывают только зависимость от текущей цены на товар. Тем не менее спрос и предложение в неабстрактных ситуациях особенно зависят от тенденции ценообразования и темпов трансформации цены. В тех моделях, где функции непрерывны и дифференцируемы по времени, эти характеристики описываются идентично первой и второй производными функции цены
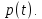
Математическая модель задачи. Для правильного понимания исследуем какой-нибудь конкретный пример. Рассмотрим движения цены продукции при условии, что прогноз спроса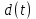 и предложения
и предложения 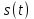 можно описать представленными ниже соотношениями:
можно описать представленными ниже соотношениями:
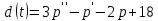 ,
,
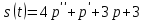 ,
,
Можем сделать вывод, что спрос увеличивается с ростом изменения цены, если темп растет, то рынок будет увеличивать спрос к товару, и наоборот. Однако экономисты считают, что стремительное увеличение цены, может отпугивать покупателя.
С учетом того, что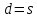 определяет некое равновесное состояние рынка мы получаем:
определяет некое равновесное состояние рынка мы получаем:
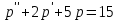 (49).
(49).
Полученное уравнение (49) является линейным неоднородным ДУ с постоянными коэффициентами.
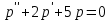 (50)
(50)
Составим для него свое характеристическое уравнение:
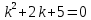 (51).
(51).
Уравнение (51) имеет решение в комплексных числах: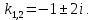 Тогда мы можем записать общее решение однородного уравнения (50) в следующем виде:
Тогда мы можем записать общее решение однородного уравнения (50) в следующем виде:
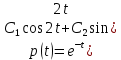 (52).
(52).
В данный момент главное отметить, что цена стремится к равновесному значению
стремится к равновесному значению 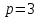 с либрациями относительно этого значения. Амплитуда этих либраций стремится к нулю при времени, стремящемся к бесконечности. [6]
с либрациями относительно этого значения. Амплитуда этих либраций стремится к нулю при времени, стремящемся к бесконечности. [6]
Решим данное уравнение и получим:
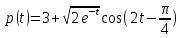 (53).
(53).
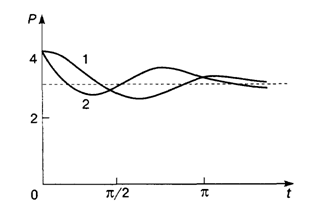
Рис.3. Модель рынка с прогнозируемыми ценами
В данной модели будем рассматривать некоторую фирму-монополиста, которая производит монотипную продукцию с особой квадратичной функцией затрат
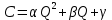 , где
, где 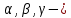 положительные некоторые постоянные, а Q – количество, выпускаемой продукции. В этом случае резерв товара не предусматривается и отсутствуют конкуренты, а выпуск всегда равен спросу. Тогда заметно, что спрос в этом случае будет зависеть и от цены
положительные некоторые постоянные, а Q – количество, выпускаемой продукции. В этом случае резерв товара не предусматривается и отсутствуют конкуренты, а выпуск всегда равен спросу. Тогда заметно, что спрос в этом случае будет зависеть и от цены 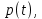 и от скорости
и от скорости 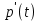 :
:
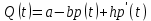 , (54)
, (54)
где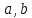 строго больше нуля, а
строго больше нуля, а  не равно нулю.
не равно нулю.
Тогда мы можем отметить, что прибыль будет зависеть от двух функций:
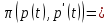
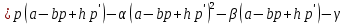 (55)
(55)
Мы считаем, что поиск некого оптимального повышения или понижения цены, которая будет увеличивать прирост дохода в определенный момент времени, нужно выдвинуть в главную цель фирму. И промежуток времени желательно взять довольно-таки коротким, чтобы функции спроса и затрат можно было считать действительно фиксированными.
Математическая модель задачи. Условия, требуемые нам могут достигаться лишь в решениях, представленных в виде уравнения Эйлера:
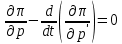 (56).
(56).
Уравнение (56) можно привести к ЛДУ второго порядка с постоянными коэффициентами и после приведения подобных членов, (56) примет вид:
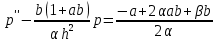 (57).
(57).
Решение задачи. Общее решение с учетом всех условий можем вычислить по формуле:
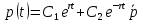 ,
,
где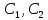 – некоторые постоянные.
– некоторые постоянные.
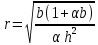 ,
,
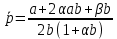 ,
,
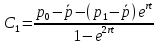 ,
, 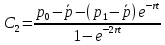 (58).
(58).
То есть, если решение данной задачи существует, то оно приведено формулами выше. Чтобы быть точно уверенными, что решение верное, нужно еще проверить условие максимума. [1]
В данной экономической модели мы исследуем формирование цены по уровню актива. Представим, что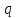 – это изменение уровня актива, тогда можем сказать, что
– это изменение уровня актива, тогда можем сказать, что  – предложение,
– предложение,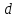 – спрос,
– спрос, 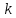 – коэффициент пропорциональности, строго больший нуля. Также изменение цены p будет пропорционально отклонению актива
– коэффициент пропорциональности, строго больший нуля. Также изменение цены p будет пропорционально отклонению актива 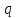 от некоего фиксированного уровня
от некоего фиксированного уровня 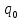 с некоторым коэффициентом пропорциональности
с некоторым коэффициентом пропорциональности  , строго большим нуля.
, строго большим нуля.
На данном этапе запишем систему ДУ, которая будет соответствовать задаче формирования по уровню актива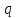 при всех вышеизложенных предположениях.
при всех вышеизложенных предположениях.
Математическая модель задачи. Если мы следуем всем данным задачи, то запишем следующую систему:
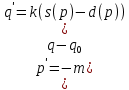 (59).
(59).
Здесь обязательно нужно учитывать, что предложение и спрос – это функции, зависящие цены.
Решение задачи. Попробуем исследовать простейший случай линейной зависимости предложения и спроса от цены:
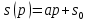 ,
,
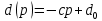 ,
,
где коэффициенты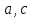 строго больше нуля.
строго больше нуля.
Тогда систему уравнений (59) мы запишем в виде:
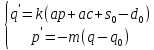 (60).
(60).
Мы пришли к системе ЛНДУ первого порядка с постоянными коэффициентами.
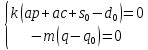 (61)
(61)
Чтобы привести данную систему к однородной системе, произведем некоторую замену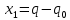 и
и 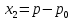 .
.
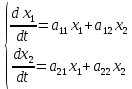 (62)
(62)
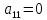
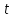 . Тогда можем точно сказать, что на данный момент времени получен доход –
. Тогда можем точно сказать, что на данный момент времени получен доход – 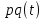 , часть которого будет тратиться на инвестиции в изготовление выпускаемой продукции, то есть
, часть которого будет тратиться на инвестиции в изготовление выпускаемой продукции, то есть 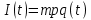 , при этом
, при этом 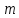 - норма инвестиции,
- норма инвестиции, 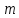 постоянна
постоянна 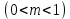 .
. Математическая модель задачи. Вследствие всех наших предположений о том, что рынок некрепкий и продукция осуществляется там полностью, мы можем отметить, что если увеличивается количество производства, то в результате получается возрастание дохода. Однако часть его будет снова тратиться для расширения выпуска товара, что в конечном итоге должно привести к увеличению стремительности выпуска. Последнее будет пропорционально увеличению инвестиций:
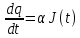 (39).
(39).Получаем ДУ:
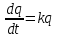 , (40).
, (40).где
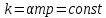 .
. Решение задачи. Здесь представленное уравнение (40) снова является ДУ с разделяющимися прямыми. Решим уравнение и получим ответ в виде:
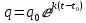 (41).
(41).Выражение (41) будет определять модель естественного роста выпуска продукции. [6]
2.8.Реклама
Математическая модель задачи. Для представления ситуации сразу рассмотрим пример. Пусть фирма реализует какой-то товар, о котором в определенный момент времени из числа потенциальных потребителей
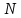 знают только
знают только  число потребителей. Можем выдвинуть предположение о том, что для увеличения продажи их продукции была дана некоторая реклама на вывесках, билбордах, радио, телевидении или в социальных сетях. Далее будем ориентироваться на то, что информация о продукции распространяется среди покупателей только «сарафанным радио», то есть только при общении покупателей друг с другом. С достаточно большой долей подлинности можно уверенно отметить, что после рекламных объявлений стремительность изменения числа о продукции пропорциональна и числу знающих, и незнающих о продукции. Далее будем стараться отсчитывать время с момента выхода рекламных объявлений, когда о товаре узнало
число потребителей. Можем выдвинуть предположение о том, что для увеличения продажи их продукции была дана некоторая реклама на вывесках, билбордах, радио, телевидении или в социальных сетях. Далее будем ориентироваться на то, что информация о продукции распространяется среди покупателей только «сарафанным радио», то есть только при общении покупателей друг с другом. С достаточно большой долей подлинности можно уверенно отметить, что после рекламных объявлений стремительность изменения числа о продукции пропорциональна и числу знающих, и незнающих о продукции. Далее будем стараться отсчитывать время с момента выхода рекламных объявлений, когда о товаре узнало
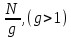 количество человек, то есть
количество человек, то есть 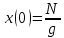 .
. Решение задачи. Вышеописанный процесс можно опишем некоторым ДУ:
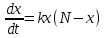 , (42)
, (42)где
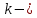 снова коэффициент пропорциональности.
снова коэффициент пропорциональности. Проинтегрируем уравнение (42) и придем к некоторой логистической кривой:
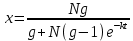 (43).
(43).Выражение, которое мы получили, позволяет нам вычислить количество людей, которые узнали о товаре, в абсолютно любой момент времени строго больший нуля. [4]
2.9.Анализ производительности труда
Представим, что на некотором предприятии рост трансформации производительности труда в определенный момент времени задается некоторым отношением:
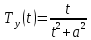 (44).
(44).Если в момент времени
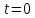 производительность труда равна
производительность труда равна 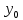 , то мы можем абсолютно точно найти закон изменения производительности труда.
, то мы можем абсолютно точно найти закон изменения производительности труда.Математическая модель задачи. Под ростом будем понимать:
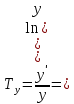 (45).
(45).Далее по условию задачи получаем некоторое дифференциальное уравнение:
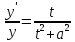 (46).
(46).Решение задачи. Представим
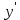 в виде дифференциалов:
в виде дифференциалов: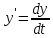 (47).
(47).Приходим снова к ДУ с разделяющимися переменными:
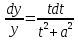 (48).
(48).Интегрируем полученное уравнение (48) и получим его решение в виде:
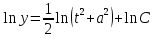 ,
,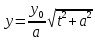 [6].
[6].2.10. Модель рынка с прогнозируемыми ценами.
В данном случае постараемся достаточно достоверно изучить модель рынка с прогнозируемыми ценами. В обыкновенных моделях рынка, спрос и предложение обычно рассчитывают только зависимость от текущей цены на товар. Тем не менее спрос и предложение в неабстрактных ситуациях особенно зависят от тенденции ценообразования и темпов трансформации цены. В тех моделях, где функции непрерывны и дифференцируемы по времени, эти характеристики описываются идентично первой и второй производными функции цены
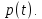
Математическая модель задачи. Для правильного понимания исследуем какой-нибудь конкретный пример. Рассмотрим движения цены продукции при условии, что прогноз спроса
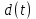 и предложения
и предложения 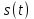 можно описать представленными ниже соотношениями:
можно описать представленными ниже соотношениями: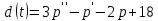 ,
,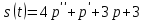 ,
,Можем сделать вывод, что спрос увеличивается с ростом изменения цены, если темп растет, то рынок будет увеличивать спрос к товару, и наоборот. Однако экономисты считают, что стремительное увеличение цены, может отпугивать покупателя.
С учетом того, что
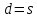 определяет некое равновесное состояние рынка мы получаем:
определяет некое равновесное состояние рынка мы получаем: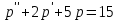 (49).
(49).Полученное уравнение (49) является линейным неоднородным ДУ с постоянными коэффициентами.
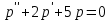 (50)
(50)Составим для него свое характеристическое уравнение:
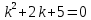 (51).
(51).Уравнение (51) имеет решение в комплексных числах:
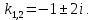 Тогда мы можем записать общее решение однородного уравнения (50) в следующем виде:
Тогда мы можем записать общее решение однородного уравнения (50) в следующем виде: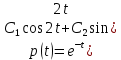 (52).
(52).В данный момент главное отметить, что цена
 стремится к равновесному значению
стремится к равновесному значению 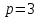 с либрациями относительно этого значения. Амплитуда этих либраций стремится к нулю при времени, стремящемся к бесконечности. [6]
с либрациями относительно этого значения. Амплитуда этих либраций стремится к нулю при времени, стремящемся к бесконечности. [6]Решим данное уравнение и получим:
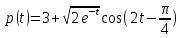 (53).
(53).
Рис.3. Модель рынка с прогнозируемыми ценами
2.11. Модель монополиста
В данной модели будем рассматривать некоторую фирму-монополиста, которая производит монотипную продукцию с особой квадратичной функцией затрат
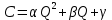 , где
, где 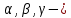 положительные некоторые постоянные, а Q – количество, выпускаемой продукции. В этом случае резерв товара не предусматривается и отсутствуют конкуренты, а выпуск всегда равен спросу. Тогда заметно, что спрос в этом случае будет зависеть и от цены
положительные некоторые постоянные, а Q – количество, выпускаемой продукции. В этом случае резерв товара не предусматривается и отсутствуют конкуренты, а выпуск всегда равен спросу. Тогда заметно, что спрос в этом случае будет зависеть и от цены 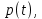 и от скорости
и от скорости 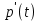 :
: 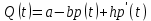 , (54)
, (54)где
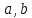 строго больше нуля, а
строго больше нуля, а 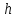 не равно нулю.
не равно нулю.Тогда мы можем отметить, что прибыль будет зависеть от двух функций:
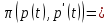
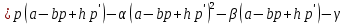 (55)
(55)Мы считаем, что поиск некого оптимального повышения или понижения цены, которая будет увеличивать прирост дохода в определенный момент времени, нужно выдвинуть в главную цель фирму. И промежуток времени желательно взять довольно-таки коротким, чтобы функции спроса и затрат можно было считать действительно фиксированными.
Математическая модель задачи. Условия, требуемые нам могут достигаться лишь в решениях, представленных в виде уравнения Эйлера:
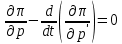 (56).
(56).Уравнение (56) можно привести к ЛДУ второго порядка с постоянными коэффициентами и после приведения подобных членов, (56) примет вид:
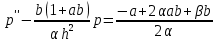 (57).
(57).Решение задачи. Общее решение с учетом всех условий можем вычислить по формуле:
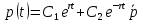 ,
,где
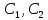 – некоторые постоянные.
– некоторые постоянные.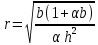 ,
,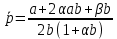 ,
,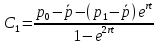 ,
, 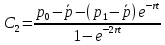 (58).
(58).То есть, если решение данной задачи существует, то оно приведено формулами выше. Чтобы быть точно уверенными, что решение верное, нужно еще проверить условие максимума. [1]
2.12. Формирование цены по уровню актива
В данной экономической модели мы исследуем формирование цены по уровню актива. Представим, что
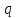 – это изменение уровня актива, тогда можем сказать, что
– это изменение уровня актива, тогда можем сказать, что  – предложение,
– предложение,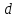 – спрос,
– спрос, 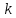 – коэффициент пропорциональности, строго больший нуля. Также изменение цены p будет пропорционально отклонению актива
– коэффициент пропорциональности, строго больший нуля. Также изменение цены p будет пропорционально отклонению актива 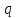 от некоего фиксированного уровня
от некоего фиксированного уровня 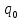 с некоторым коэффициентом пропорциональности
с некоторым коэффициентом пропорциональности  , строго большим нуля.
, строго большим нуля. На данном этапе запишем систему ДУ, которая будет соответствовать задаче формирования по уровню актива
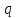 при всех вышеизложенных предположениях.
при всех вышеизложенных предположениях.Математическая модель задачи. Если мы следуем всем данным задачи, то запишем следующую систему:
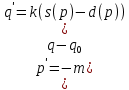 (59).
(59).Здесь обязательно нужно учитывать, что предложение и спрос – это функции, зависящие цены.
Решение задачи. Попробуем исследовать простейший случай линейной зависимости предложения и спроса от цены:
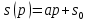 ,
,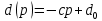 ,
,где коэффициенты
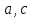 строго больше нуля.
строго больше нуля.Тогда систему уравнений (59) мы запишем в виде:
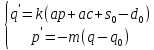 (60).
(60).Мы пришли к системе ЛНДУ первого порядка с постоянными коэффициентами.
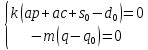 (61)
(61)Чтобы привести данную систему к однородной системе, произведем некоторую замену
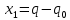 и
и 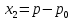 .
.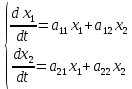 (62)
(62)