Файл: Курсовая работа применение дифференциальных уравнений к решению экономических задач Обучающийся 4 курса.docx
Добавлен: 11.01.2024
Просмотров: 281
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
2.Задачи экономики, приводящиеся к дифференциальным уравнениям
2.1.Рост общественного благосостояния (модель Золотаса)
2.2.Модель экономического роста (Модель Солоу)
2.3.Динамика рыночной цены (модель Самуэльсона)
2.6.Интенсивность выпуска продукции
2.7.Естественный рост выпуска продукции
2.9.Анализ производительности труда
2.10. Модель рынка с прогнозируемыми ценами.
, 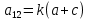 ,
, 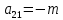 ,
, 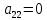 .
.
Общее решение запишем в виде:
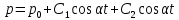 ,
, 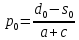 (63),
(63),
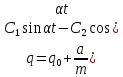 (64).
(64).
Представим, что первоначальная цена равна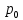 , то есть можем сделать вывод, что
, то есть можем сделать вывод, что
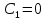
Тогда соотношение между ценой и уровнем актива запишем в следующем виде:
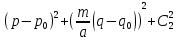 (65).
(65).
Здесь можно заметить, что эта кривая описывает меняющееся равновесие обозреваемого процесса. Далее мы подставляем в последнее уравнение точные значения, которые возьмем в некоторый определенный момент времени и можем достаточно точно идентифицировать эту кривую. Для того, чтобы нам располагаться в отмеченном равновесном состоянии, нам стоит выяснить величину цены с помощью уровня актива по следующей формуле:
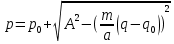 (66). [6]
(66). [6]
Математическое исследование закономерностей реального мира сплошь и рядом приводит к уравнениям, которые связывают неизвестные величины и их производные, то есть к дифференциальным уравнениям различных типов.
В ходе написания курсовой работы мы нашли и использовали разнообразнейшие методы использования дифференциальных уравнений в экономических задач, а также изучили различные экономические модели.
Мы проанализировали применение дифференциальных уравнений в экономике и экономических задачах. Исследовав множество моделей, можно сделать выводы, что самой широко используемыми являются те модели, которые применяются в теории фирмы и рынке. В границах этой теории было рассмотрено, каким образом используются дифференциальные уравнения в движении естественного темпа выпуска продукции, рекламе, динамике рыночной цены, интенсивности выпуска продукции и т.д.
Таким образом, дифференциальные уравнения действительно широко применяются к решению экономических задачах в разнообразных моделях экономики, где исследуется зависимость переменных от времени. Дифференциальные уравнения являются одним из нередко употребляемых видов вычислений в жизнедеятельности индивида.
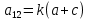 ,
, 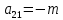 ,
, 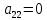 .
.Общее решение запишем в виде:
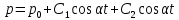 ,
, 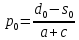 (63),
(63),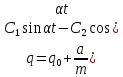 (64).
(64).Представим, что первоначальная цена равна
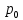 , то есть можем сделать вывод, что
, то есть можем сделать вывод, что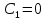
Тогда соотношение между ценой и уровнем актива запишем в следующем виде:
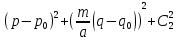 (65).
(65).Здесь можно заметить, что эта кривая описывает меняющееся равновесие обозреваемого процесса. Далее мы подставляем в последнее уравнение точные значения, которые возьмем в некоторый определенный момент времени и можем достаточно точно идентифицировать эту кривую. Для того, чтобы нам располагаться в отмеченном равновесном состоянии, нам стоит выяснить величину цены с помощью уровня актива по следующей формуле:
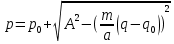 (66). [6]
(66). [6]Заключение
Математическое исследование закономерностей реального мира сплошь и рядом приводит к уравнениям, которые связывают неизвестные величины и их производные, то есть к дифференциальным уравнениям различных типов.
В ходе написания курсовой работы мы нашли и использовали разнообразнейшие методы использования дифференциальных уравнений в экономических задач, а также изучили различные экономические модели.
Мы проанализировали применение дифференциальных уравнений в экономике и экономических задачах. Исследовав множество моделей, можно сделать выводы, что самой широко используемыми являются те модели, которые применяются в теории фирмы и рынке. В границах этой теории было рассмотрено, каким образом используются дифференциальные уравнения в движении естественного темпа выпуска продукции, рекламе, динамике рыночной цены, интенсивности выпуска продукции и т.д.
Таким образом, дифференциальные уравнения действительно широко применяются к решению экономических задачах в разнообразных моделях экономики, где исследуется зависимость переменных от времени. Дифференциальные уравнения являются одним из нередко употребляемых видов вычислений в жизнедеятельности индивида.
Список использованных источников
-
Бугров Я.С. Высшая математика: учеб. для студентов инженерно-технических специальностей вузов / Я.С. Бугров, С.М. Никольский – Москва, 2007. – 511 с. -
Дифференциальные уравнения как инструмент исследования прикладных экономических задач [Электронный ресурс] – URL: https://bstudy.net/712954/pedagogika/differentsialnye_uravneniya_instrument_issledovaniya_prikladnyh_ekonomicheskih_zadach (дата обращения 28.03.2022). -
Жегалов В.И. Приложения обыкновенных дифференциальных уравнений: учебное пособие / В.И. Жегалов, С.Н. Киясов – Издательство Казанского Государственного Университета, 2007. – 179 с. -
Королев А.В. Экономико-математические методы и моделирование : учебник и практикум для бакалавриата и магистратуры / А. В. Королев — М. : Издательство Юрайт, 2016. – 280 с. -
Краснов М.Л. Обыкновенные дифференциальные уравнения: учебник для технических вузов / М.Л. Краснов, А.И. Киселев, Г.И. Макаренко – Москва, 2009. – 259 с. -
Красс М.С., Чупрынов Б.П. Основы математики и ее приложения в экономическом образовании. [Электронный ресурс] – URL: https://matica.org.ua/metodichki-i-knigi-po-matematike/osnovy-matematiki-i-ee-prilozheniia-v-ekonomicheskom-obrazovanii-krass-m-s-chuprynov-b-p (дата обращения 05.04.2022) -
Линейные дифференциальные уравнения. [Электронный ресурс] – URL: http://www.mathprofi.ru/lineinye_differencialnye_uravnenija.html (дата обращения 11.04.2022) -
Модуль Самуэльсона. [Электронный ресурс] – URL: https://studme.org/263978/ekonomika/model_samuelsona_hiksa (дата обращения 16.04.2022) -
Сабитов К.Б. Функциональные, дифференциальные и интегральные уравнения: учебное пособие / К.Б. Сабитов – М: Высшая школа, 2005. – 671 с. -
Самойленко А.М. Дифференциальные уравнения: примеры и задачи: учебное пособие / А.М. Самойленко, С.А. Кривошея, Н.А. Перестюк – Москва, 1989. – 464 с.