Файл: Курсовая работа применение дифференциальных уравнений к решению экономических задач Обучающийся 4 курса.docx
Добавлен: 11.01.2024
Просмотров: 269
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
2.Задачи экономики, приводящиеся к дифференциальным уравнениям
2.1.Рост общественного благосостояния (модель Золотаса)
2.2.Модель экономического роста (Модель Солоу)
2.3.Динамика рыночной цены (модель Самуэльсона)
2.6.Интенсивность выпуска продукции
2.7.Естественный рост выпуска продукции
2.9.Анализ производительности труда
2.10. Модель рынка с прогнозируемыми ценами.
Министерство науки и высшего образования Российской Федерации
Федеральное государственное автономное образовательное учреждение
высшего образования
«КАЗАНСКИЙ (ПРИВОЛЖСКИЙ) ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»
Елабужский институт (филиал)
Отделение математики и естественных наук
Кафедра математики и прикладной информатики
Направление подготовки (специальность): 44.03.05 Педагогическое образование (с двумя профилями подготовки)
Профиль (специализация): Математика и физика
КУРСОВАЯ РАБОТА
Применение дифференциальных уравнений к решению экономических задач
| Обучающийся 4 курса группы е8211 «___»__________20__г. | Тарасенко Е.Д. |
| Научный руководитель к.ф.-м.н., доцент «___»__________20__г. | Созонтова Е.А. |
Елабуга - 2022
Содержание
Введение 3
1.Дифференциальные уравнения 5
2.Задачи экономики, приводящиеся к дифференциальным уравнениям 6
2.1.Рост общественного благосостояния (модель Золотаса) 6
2.2.Модель экономического роста (Модель Солоу) 8
2.3.Динамика рыночной цены (модель Самуэльсона) 9
2.4.Движение фондов 10
2.5.Динамика потребителей 12
2.6.Интенсивность выпуска продукции 13
2.7.Естественный рост выпуска продукции 14
2.8.Реклама 15
2.9.Анализ производительности труда 16
2.10. Модель рынка с прогнозируемыми ценами. 17
2.11. Модель монополиста 18
2.12. Формирование цены по уровню актива 20
Заключение 23
Список использованных источников 24
Введение
Современная публицистика подчёркивает глубокую взаимосвязанность математических методов с задачами экономики и физики. В первую очередь, это обусловлено тем, что в последнее время огромное внимание уделяется особым связям математики с экономикой, а также с другими социально-экономическими науками. Можем отметить, что они отражаются не только при решении некоторых практических задач, но также и в фундаментальных науках в целом.
Дифференциальные уравнения широко применяются к решению экономических задачах в разнообразных моделях экономики, где исследуется зависимость переменных от времени. Таких моделей некоторое множество, среди которых: модель Эванса, с её помощью мы можем установить уравновешенность ценового рынка одного товара; также модель Солоу, которая отображает экономический рост в целом и многие другие.
Актуальность данной работы заключается в изучении использования дифференциальных уравнений в экономических задачах и экономике в целом.
В цель курсовой работы можно выделить поиск разнообразнейших методов использования дифференциальных уравнений в экономических задач, изучение различных экономических моделей.
В соответствие с целью курсовой работы были поставлены следующие задачи:
-
Найти и исследовать литературу по этой теме; -
Накопить и упорядочить приобретённую информацию; -
Обобщить полученные знания; -
Использовать дифференциальные уравнения для всевозможных экономических моделей и задач.
1.Дифференциальные уравнения
Дифференциальным уравнением (далее ДУ) называется уравнение, связывающее данную функцию одной или нескольких переменных, эти переменные и производные различных порядков данной функции. [9]
Простейшим примером дифференциального уравнения является уравнение
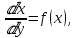 (1)
(1)где
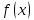 – известная, а
– известная, а 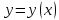 – искомая функции независимого переменного
– искомая функции независимого переменного 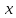 . Решения этого уравнения называют первообразными функциями для функции
. Решения этого уравнения называют первообразными функциями для функции 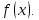 [10]
[10]Разберем некоторые вопросы теории дифференциальных уравнений на примере уравнений первого порядка, которые мы можем решить относительно производной, т.е. представить в виде
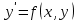 , (2)
, (2)где f - некоторая функция нескольких переменных.
1.Теорема существования и единственности решения дифференциального уравнения.
Пусть в дифференциальном уравнении (2) функция
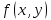 и ее частная производная
и ее частная производная 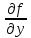 непрерывны на открытом множестве G координатной плоскости Оху. Тогда для всякой точки
непрерывны на открытом множестве G координатной плоскости Оху. Тогда для всякой точки 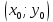 множества G найдется решение
множества G найдется решение  уравнения (2), удовлетворяющее условию
уравнения (2), удовлетворяющее условию 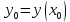 . [5]
. [5]Если два решения
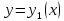 и
и 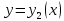 уравнения (1) совпадают хотя бы для одного значения
уравнения (1) совпадают хотя бы для одного значения 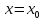 , т.е. если
, т.е. если 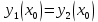 , то эти решения совпадают для всех тех значений переменной
, то эти решения совпадают для всех тех значений переменной  , для которых они определены. Дифференциальное уравнение первого порядка называется уравнением с разделяющимися переменными, если оно может быть представлено в виде
, для которых они определены. Дифференциальное уравнение первого порядка называется уравнением с разделяющимися переменными, если оно может быть представлено в виде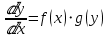 (3)
(3)или в виде
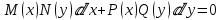 , (4)
, (4)где
 ,
, 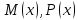 - некоторые функции переменной х,
- некоторые функции переменной х, 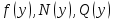 - функции переменной у.
- функции переменной у. Можем выделить характерное свойство дифференциальных уравнений. Мы заметили, что дифференциальное уравнение имеет бесконечное множество решений. Поэтому, решив дифференциальное уравнение, которое описывает некоторый процесс, нельзя единовременно найти зависимость между величинами, обрисовывающими некий процесс. Чтобы выделить из огромного множества зависимостей ту, которая описывает нужный нам процесс, обязательно достаточно иметь какую-то дополнительную информацию, например знать начальное состояние данного процесса. [10]
2.Задачи экономики, приводящиеся к дифференциальным уравнениям
Дифференциальные уравнения мы можем применять при решении разнообразных типов экономических задач, которые можно представить в качестве моделей или определенного вида задачи.
2.1.Рост общественного благосостояния (модель Золотаса)
Известный греческий экономист Ксенофонт Золотас в 1981 году в своей книге «Economic Growth and Declining Social Welfare» выдвинул идею о том, что производство большого количества товаров практически никогда не приводит к лучшей жизни. В своей работе экономист выделил два фактора, каждый из которых действует с определенной относительной интенсивностью в зависимости от приобретенного уровня общественного благосостояния. Т.е. Золотас считает, что присутствует два фактора: один, который сдерживает развитие, второй – стимулирует. [6]
Математическая модель задачи. Представим, что
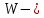 уровень общественного благосостояния в целом. Тогда если возьмем
уровень общественного благосостояния в целом. Тогда если возьмем 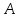 , как некоторую критическую точку, то сдерживающим для модели фактором будет считаться
, как некоторую критическую точку, то сдерживающим для модели фактором будет считаться 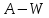 , а стимулирующим
, а стимулирующим 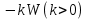 . Вследствие этого динамику уровня благосостояния мы можем выразить через ДУ:
. Вследствие этого динамику уровня благосостояния мы можем выразить через ДУ: 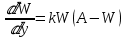 , (5) , (5) |
где
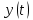 будет считаться доходом на одну душу населения. [2] Данное уравнение представляет модель Золотаса.
будет считаться доходом на одну душу населения. [2] Данное уравнение представляет модель Золотаса.Решение задачи. Интегрирование уравнения (5) приводит к данному решению
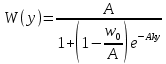 , (6) , (6)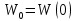 (7). (7).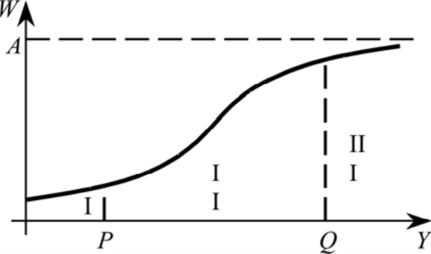 Рис.1 Уровень общественного благосостояния | 2 |
Решение ДУ (5) является уравнением некоторой логической кривой. В ходе разработки Золотас сделал вывод о том, что существует три стадии развития общества:
1 ˗ «общество нужды»;
2 ˗ «общество постоянных улучшений»;
3 - «общество снижающихся темпов роста благосостояния», где постоянные Pи Qбудут определять некоторые уровни доходов.
2.2.Модель экономического роста (Модель Солоу)
Модель Солоу считается первичной точкой для большинства новейших моделей экономического роста, которым она фактически дала настоятельную математическую базу для анализирования роста трансформации капитала. Как оказалось, данная модель очень серьезно повлияла на всю экономическую теорию в целом. [3]
Рассмотрим модель, в которой производственные фонды
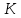 и трудовые ресурсы
и трудовые ресурсы 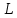 взаимоcвязаны некоторым соотношением
взаимоcвязаны некоторым соотношением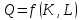 , (8)
, (8)где
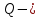 конечный продукт (выпуск), а
конечный продукт (выпуск), а 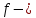 производственная функция.
производственная функция. Математическая модель задачи. При решении данной модели мы можем предположить, что
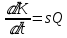 (9), причем
(9), причем 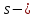 доля сбережений в доходе, и
доля сбережений в доходе, и 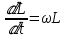 (10), где
(10), где 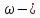 темп роста
темп роста 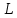 . Меняющаяся сущность наших предположений состоит в том, что определяются не сами уровни значений
. Меняющаяся сущность наших предположений состоит в том, что определяются не сами уровни значений 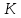 и
и 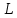 , а именно скорости их трансформации.
, а именно скорости их трансформации. Решение задачи. В качестве производственной функции удобнее будет ориентироваться на всемирно известную функцию Кобба-Дугласа:
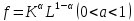 . Если мы обозначим
. Если мы обозначим 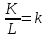 , то производственную функцию перепишем в виде:
, то производственную функцию перепишем в виде: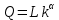 (9).
(9).Ввиду того, что