Файл: Научнопрактическая коференция Шаг в будущее Применение программы Живая математика Построение квадрата по четырем точкам.docx

Научно-практическая коференция

«Шаг в будущее»

Применение программы «Живая математика»

Построение квадрата по четырем точкам

Исполнитель проекта

Черноградская Ая

МБОУ «Крест - Хальджайская средняя общеобразовательная школа

им.Героя Советского Союза Ф. М. Охлопкова», 11 класса

с. Крест – Хальджай, Томпонский район

Республика Саха (Якутия)

Преподаватель:

Бравина Лилия Николаевна,

учитель математики

Научный консультант:

Ефремов Валентин Павлович - кандидат педагогических наук, доцент кафедры методики преподавания математики ИМиИ СВФУ

2021

Оглавление

1. 
   Введение …………………………………………………………………………
   
2. 
   Теоретическая часть………………………………………………………………
   
3. 
   Экспериментально – практическая часть ………………………………………
   
4. 
   Вывод ……….………………………………………………………………………
   
5. 
   Литература ………………………………………………………………………
   

Введение

Актуальность:

В школе, когда проходили задачи на построение, меня очень заинтересовало

решение таких задач. При решении подобных задач есть множество исследовательских способов решения. Задача «Квадрат по 4 точкам. На плоскости отмечены 4 точки. Построить квадрат, на сторонах которого лежат эти точки» рекомендована Ефремовым Валентином Павловичем - кандидатом педагогических наук, доцентом кафедры методики преподавания математики ИМиИ СВФУ. В этом году мы продолжили исследовательскую работу по поиску новых вариантов решения с дальнейшим применением программы «Живая геометрия»

Проблема:

Через любые 4 точки, не лежащие на одной прямой, можно ли построить квадрат, на сторонах которого лежат эти точки.

Новизна:

Решение этой задачи не опубликовано в математических сборниках. При исследовании задачи применяется программа «Живая геометрия».

Предмет исследования:

Рассмотреть возможные варианты, если через любые 4 точки, из которых никакие три точки не лежат на одной прямой, построить квадрат, на сторонах которого лежат эти точки.

Цель:

Исследовать условие существования решений с помощью учебной программы «Живая геометрия».

---

Задачи:

1) построить квадрат через любые 4 точки, из которых никакие три точки не лежат на одной прямой, на сторонах которого лежат эти точки.

2) найти решения всех возможных вариантов;

Теоретическая часть

В задачах на построение рассматриваются множество всех точек плоскости, множество всех прямых плоскости и множество всех окружностей плоскости, над которыми допускаются следующие операции:

1. 
   Выделить точку из множества всех точек:
   
   1. 
      произвольную точку
      
   2. 
      произвольную точку на заданной прямой
      
   3. 
      произвольную точку на заданной окружности
      
   4. 
      точку пересечения двух заданных прямых
      
   5. 
      точки пересечения/касания заданной прямой и заданной окружности
      
   6. 
      точки пересечения/касания двух заданных окружностей
      
2. 
   «С помощью линейки» выделить прямую из множества всех прямых:
   
   1. 
      произвольную прямую
      
   2. 
      произвольную прямую, проходящую через заданную точку
      
   3. 
      прямую, проходящую через две заданных точки
      
3. 
   «С помощью циркуля» выделить окружность из множества всех окружностей:
   
   1. 
      произвольную окружность
      
   2. 
      произвольную окружность с центром в заданной точке
      
   3. 
      произвольную окружность с радиусом, равным расстоянию между двумя заданными точками
      
   4. 
      окружность с центром в заданной точке и с радиусом, равным расстоянию между двумя заданными точками
      

В условиях задачи задается некоторое множество точек. Требуется с помощью конечного количества операций из числа перечисленных выше допустимых операций построить другое множество точек, находящееся в заданном соотношении с исходным множеством.

Решение задачи на построение содержит в себе три существенные части:

1. 
   Описание способа построения заданного множества.
   
2. 
   Доказательство того, что множество, построенное описанным способом, действительно находится в заданном соотношении с исходным множеством. Обычно доказательство построения производится как обычное доказательство теоремы, опирающееся на аксиомы и другие доказанные теоремы.
   
3. 
   Анализ описанного способа построения на предмет его применимости к разным вариантам начальных условий, а также на предмет единственности или неединственности решения, получаемого описанным способом.
   

В задачах на построение речь идет о построении геометрических фигур (отрезок, угол, пара параллельных прямых и т. д.) с помощью некоторых инструментов.

---

Решить задачу на построение – это значит найти способ построения фигуры, осуществить это построение и доказать, что построенная фигура – фигура, обладающая требуемыми свойствами.

В данном разделе мы будем решать задачи на построение «основных» геометрических фигур с помощью линейки и циркуля. Построение сложных фигур с помощью предварительного анализа можно будет свести к последовательности построений «основных» фигур.

Для начала мы должны описать, что можно делать с помощью линейки и циркуля.

Линейка – инструмент, позволяющий:

• 
  провести произвольную прямую;
  
• 
  провести прямую (произвольную), проходящую через данную точку;
  
• 
  провести прямую, проходящую через две данные точки;
  
• 
  построить произвольный луч;
  
• 
  построить произвольный луч с заданным началом;
  
• 
  построить луч с заданным началом, проходящий через заданную точку;
  
• 
  построить отрезок с заданными концами.
  

Циркуль – инструмент, позволяющий:

• 
  построить произвольную окружность;
  
• 
  построить окружность с заданным радиусом;
  
• 
  построить окружность с заданным центром и радиусом;
  
• 
  отложить данный отрезок на прямой от данной точки.
  

Ход работы:

При решении этой задачи применяем определение и свойства квадрата.

Квадрат-это прямоугольник, у которого все стороны равны.

Свойства:

• 
  1. Все углы квадрата прямые.
  
• 
  Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.
  

рис 1

• 
  2. Если в квадрате EK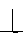 FL , то их длины равны, т.е │EK│=│FL│ (рис1). Это свойство в школе не рассматривали. Приводим примером задачу, которую мы применяем в ходе исследования задачи.
  

Задача: (Н.В. Аргунова, Е.П.Жирков «Элементарная математика»)

Две взаимно перпендикулярные прямые пересекают стороны АВ,ВС, СД и АД квадрата АВСД соответственно в точках Е, F, K, L. Докажите, что ЕК=FL

(рис. 1).

Решение. На этом примере покажем применение геометрического метода.

1) Проведем FM || СД и КР || АД.

2) Тогда отрезки ЕК и FL станут сторонами двух треугольников ЕКР и FLM (рис.1), и, значит, достаточно доказать равенство этих треугольников.

---

3) Имеем РК=FM (как высоты квадрата), ∠LFM=∠EKP (как углы с взаимно перпендикулярными сторонами).

4) Значит ΔEKP= ΔFLM (по катету и острому углу).

5) Из равенства прямоугольных треугольников следует равенство их гипотенуз, т.е. EK=FL. Что и требовалось доказать.

Часть I

Задача: Квадрат по 4 точкам. На плоскости отмечены 4 точки. Построить квадрат, на сторонах которого лежат эти точки.

I . Анализ

Предположим, что задача решена.

а) пусть эти точки лежат на сторонах квадрата;

б) середины диагоналей Q и P четырехугольника АВСД лежат на осях симметрии искомого квадрата (по 2 свойству) ДР=PB.

в) на перпендикуляр к диагонали ДВ, проведенном через точку Q отложим отрезок QM=PB.

г) М и В при этом лежат на соседних сторонах квадрата, каждая прямая пересекает параллельные стороны квадрата.

II. Построение :

1. А,В,С,Д – из них 3 точки не лежат на одной прямой с четвертой точкой	2. А соединяем с Д, В соединяем с точкой С, отрезки АВ и ВС
3. Находим середины отрезков АД и ВС, то АР=РД, CQ=QВ	4. Середины отрезков лежат на осях симметрии искомого квадрата
5. Через Q проводим прямую j параллельной прямой ВР. Прямая j перпендикулярна к отрезку АВ	6. Отложим отрезок QM=PД на прямой j. Через М и В проводим прямую n, и построим квадрат.

III. Исследование:

При исследовании задачи мы применили учебную программу «Живая математика» и построение с помощью циркуля.

---

И нашли такие варианты решения.

1. Квадрат можно построить , когда две соседние углы тупые.

1.1 При построении квадрата применяем свойства перпендикулярности прямых

а) соединяем противоположные точки А и С, В и Д

б) Из точки А и С проводим перпендикуляры, то FD=GK

в) соединяем точки К и С, и к прямой КС проводи м перпендикуляры из точек Д и В, а из точки А проводи м параллельную прямую YX и получаем искомый квадрат.


K




1.2 При построении

а) Соединим соседние точки ЕН

б) Из точек F и G проведем перпендикуляр к отрезку ЕН

в) В четырехугольнике FPNG проведем диагональ FN

г) Через точки E и G проведем параллельную диагонали прямую.

д) Из точки F проведем перпендикуляр к отрезку RS

е) Через точку Н проведем прямую параллельную QR



2.1 При построение квадрата применяем свойство параллельности прямых

а) АС и ВД диагонали четырехугольника АВСД

б) Находим середины отрезков АС и ВД, то АH=HC, BT=TD

в) середины диагоналей лежат на осях симметрии искомого квадрата

г) через L проводим параллельную прямую j.

д) Отложим отрезок ТД=HG. Через G и C проводим прямую LK, и к прямой LK проводим из точек В и Д перпендикуляры и построим искомый квадрат.

г) через L проводим параллельную прямую j.

д) Отложим отрезок ТД=HG. Через G и C проводим прямую LK, и к прямой LK проводим из точек В и Д перпендикуляры и построим искомый квадрат.




2.2 При построении:

а) проводим диагонали

б) из точек В и U проводим перпендикуляры к диагоналям

в) через точки А и Д проводим прямые параллельно к прямой ВК,

г) через точки В и U проводим прямые параллельно к прямой АД,



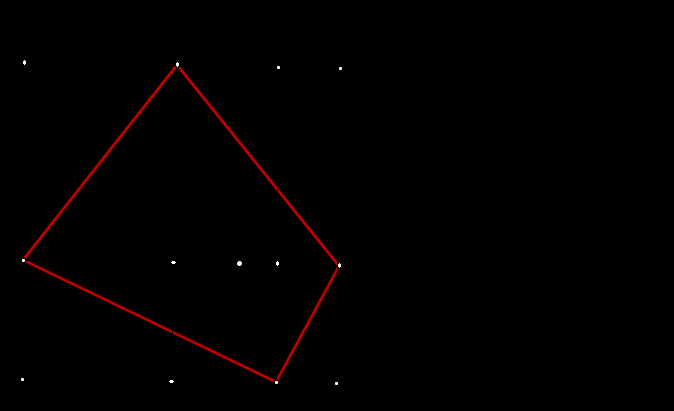
3.1 При построении квадрата применяем пересечение окружности.

При построении:

а) соединяем соседние точки А и В, С и Д

б) находим середины отрезков АВ и СД, то ОА = OB=L, CО=ОД=P и проводим окружности с радиусом L и P

---