Файл: Научнопрактическая коференция Шаг в будущее Применение программы Живая математика Построение квадрата по четырем точкам.docx

в) через середины отрезков АВ и СД проводим серединные перпендикуляры

г) М и R являются точками пересечения с окружностями

д) М и В соединяем прямой, и проводим перпендикуляры МА и УС и построим искомый квадрат



3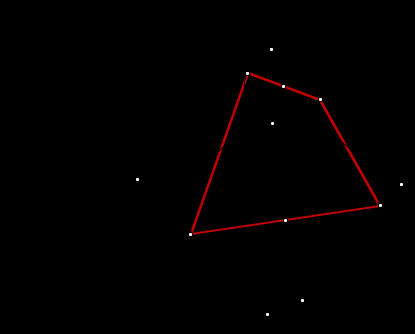 .2 Если один угол тупой , остальные углы острые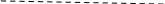



4.1 При построении квадрата применяем свойства биссектрис угла:

а) Из точек R и Q проведем перпендикуляры к противоположным отрезкам

б) Из углов PF1R и QG1S проведем биссектрисы

в) Через точку Р проведем параллельный биссектрисе отрезок К1Н1

г) Из точек R и S проведем перпендикуляр к отрезку К1Н1

д) Из точки Q проведем перпендикуляр к отрезку К1J1



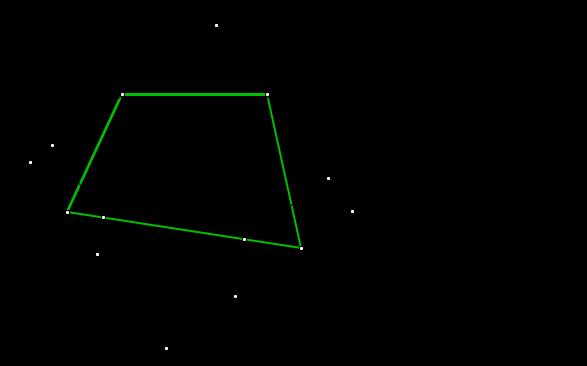
5. Исследование, когда нельзя построить квадрат.

5.1 Если два соседних угла тупые, а один из оставшихся углов меньше 45 градусов, то построение квадрата будет несколько иным, при этом две точки лежат на одной из сторон квадрата, а одна сторона окажется обделенной.



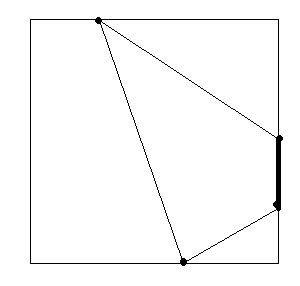
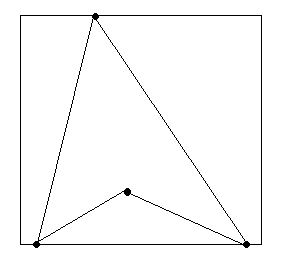
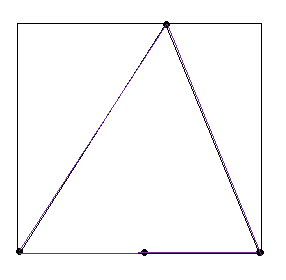
5.2 Если три точки лежат на одной линии, а четвертая соединена с двумя крайними, то на образовавшемся треугольнике можно построить квадрат только в том случае, если высота, опущенная из точки, лежащей на параллельной стороне , на сторону с тремя точками, то можно построить квадрат, но по условию задачи не имеет решения.(рис2)

Выводы:

Выполнив исследование с помощью обучающей программы «Живая геометрия» и построение с циркулем, можно сделать такие выводы:

1. Если на фигуре, образованной точками, где два соседних угла тупые, то можно найти несколько вариантов построения искомого квадрата.

---

2. Если один угол тупой, то имеется одно решение.

3. Если два соседних угла тупые, а один из оставшихся углов меньше 45 градусов, то построение квадрата будет несколько иным, при этом две точки лежат на одной из сторон квадрата, а одна сторона окажется обделенной.

4. Если три точки лежат на одной линии, а четвертая соединена с двумя крайними, то на образовавшемся треугольнике можно построить квадрат только в том случае, если высота, опущенная из точки , лежащей на параллельной стороне , на сторону с тремя точками, то можно построить квадрат, но по условию задачи не имеет решения.

5. Квадрат невозможно построить, если фигура образованная этими точками, имеет острые углы .

6. Квадрат невозможно построить, если две точки расположены ниже двух других.

7. Квадрат невозможно построить , если противоположные углы тупые.

Использованная литература:

1.Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б и др. Геометрия 7-9: М.: Просвещение, 2016

2. Аргунова Н.В., Жирков Е.П.. Элементарная математика. Ч.2: учебное пособие для самостоятельной работы студентов. Якутск, 2008

3.Генкин С. А. и др. Ленинградские математические кружки. - Киров: издательство "АСА", 1994.
4. Готман Э.Г., Скопец З.А. Задача одна - решения разные. Просвещение, 2011

 5. Игудисман О.С. Математика на устном экзамене.

М.: Айрис-пресс, 2002.

6. Костовский А.Н. Геометрические построения одним циркулем. М.:Наука, 1989

7. Фарков А.В. Учимся решать олимпиадные задачи.М.:

Айрис-пресс, 2007

8.Факультативный курс по математике. 7-9 / Сост. И. Л. Никольская. — М.: Просвещение, 1991 .

9. Фридман Л.М., Турецкий Е.И. Как научиться решать задачи. - М.: Просвещение, 1989

Часть II

В прошлом году мы, в основном, работали над построением квадрата по любым 4 точкам в плоскости. Рассмотрев несколько вариантов решения подобных задач, мы обратили внимание на перпендикулярные прямые, которые не лежат в центре квадрата. Поэтому при построении квадрата у нас возникли следующие вопросы:

1. Возможно ли так выбирать точки на сторонах квадрата, чтобы окружности касались?

---

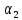
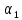
2. При каком расположении точек на сторонах квадрата окружности 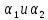, описанные около четырехугольников ATDN и CSBN, касаются в центре N квадрата SLTK .

Составим задачу 1. Дан квадрат SLNK, N – его центр. На сторонах LS и SK равные отрезки LB =SC. Построены точки А и D, пересечения прямых CN и BN со сторонами LT и NK. Доказать, что четырехугольники ATDN и CSBN вписаны в окружности, которые касаются в точке N.

Решение:

1. АD и BC – диаметры окружностей 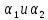. Проведем биссектрису угла АТD, биссектриса пересекается с окружностью в точке N.








2. То 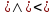CNB = 90˚, углы, опирающиеся на диаметр, прямые.

3. Около четырехугольников ATDN и CSBN, 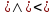DTA=90˚, когда сумма его противоположных углов равна 180˚, можно описать окружность.

4. Тогда BD ┴ АС =N, окружности 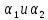касаются в одной точке.

Вывод1. Мы получили необходимое условие касания окружностей 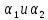, остается доказать достаточность условия . Доказательство состоит из двух частей.

Во-первых, нужно доказать, что такое расположение точек возможно.

Во-вторых, при таком выборе точек окружности 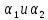, действительно касаются.

Задача 2: Дан угол с вершиной В. Построены всевозможные окружности, каждая из которых проходит через вершину В и пересекает сторону угла в таких точках Д и Е, что сумма ВД+ ВЕ=m, где m- данный отрезок.

Решение:


β

---

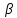
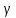
1. Пусть окружность удовлетворяет условию задачи, т.е. ВД+ ВЕ=m.

2. Проведем биссектрису данного угла, и пусть она пересечет 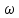в точке О.

3. Около четырехугольника ВДОЕ можно описать окружность. Обозначим радиус окружности через R и

.

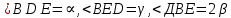4. 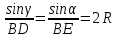, тогда 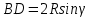, BE= ,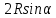

5. ВД+ ВЕ= 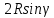+ 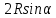= = 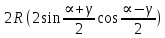= =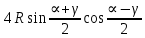 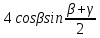m,

так как ,

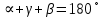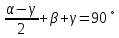
6. Тогда ВО= 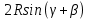. Из полученных равенств следует, что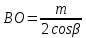

Вывод 2. Длина отрезка ВО не зависит от выбора окружности, поэтому все окружности проходят через точку О. Геометрический смысл точки О мы уже знаем – это центр окружности, описанной около четырехугольника ВДОЕ.

Выводы:

1. Возможно ли так выбирать точки на сторонах квадрата, чтобы окружности касались?

2. При каком расположении точек на сторонах квадрата окружности , описанные около четырехугольников, касаются в центре квадрата .

Вывод1. Мы получили необходимое условие касания окружностей . Окружности 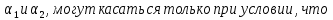отрезки АС и ВД пересекаются в центре О

Остается доказать достаточность условия Доказательство состоит из двух частей.

---

Во-первых, нужно доказать, что такое расположение точек возможно.

Во-вторых, при таком выборе точек окружности , действительно касаются.

Вывод 2. Длина отрезка ВО не зависит от выбора окружности, поэтому все окружности проходят через точку О. Геометрический смысл точки О мы уже знаем – это центр окружности, описанной около четырехугольника ВДОЕ.

1.1 Все окружности пересекаются в центре О, АС = ВД и перпендикулярны.

1.2 Если окружности пересекаются в одной точке О, то АС и ВД перпендикулярны

1.3 Если треугольник ВСД – равнобедренный, то биссектриса проходит через центр квадрата.

1.4.Если все окружности не пересекаются в центре О, то отрезки АС и ВД не перпендикулярны

Вывод 3 :

1. Окружности касаются в одной точке, если одна из биссектрис пройдет через центр квадрата.

2. Окружности касаются в одной точке, если общий серединный перпендикуляр АС и ВД проходит через центр N.

Вывод 4. Если в квадрате противолежащие прямоугольные треугольники, сумма катетов в которых в 2 раза больше, чем сторона квадрата, то эти отрезки АС и ВД перпендикулярны.

Приложение

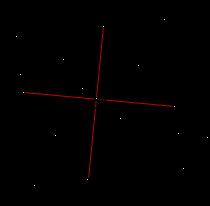
Теперь исследуем по программе «Живая геометрия»

1.1 Все окружности пересекаются в центре N, LK=TS и перпендикулярны.



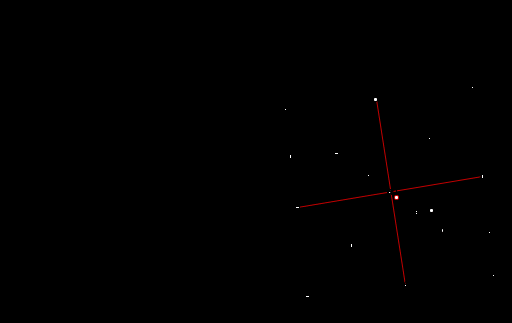
1.2 Если окружности пересекаются в одной точке 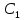, то АС и ВД перпендикулярны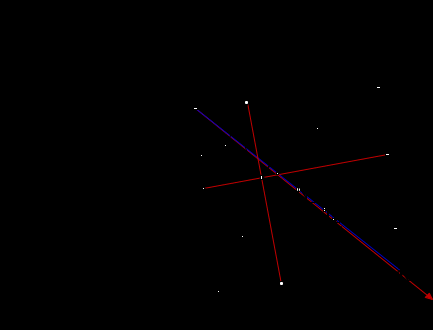



Вывод 3 :

1. Окружности касаются в одной точке, если одна из биссектрис пройдет через центр квадрата.

2. Окружности касаются в одной точке, если общий серединный перпендикуляр BD и CA проходит через центр N.

1.3 Если треугольник ВСД – равнобедренный, то биссектриса проходит через центр квадрата.



1.4



Вывод 4. Если в квадрате противолежащие прямоугольные треугольники, сумма катетов в которых в 2 раза больше, чем сторона квадрата, то эти отрезки * перпендикулярны.

Подобную задачу мы решили несколькими вариантами

---