Файл: Методические указания к практическим работам для студентов направления 21. 03. 01.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 289
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
ПОРОДЫ-КОЛЛЕКТОРЫ НЕФТИ И ГАЗА
РАСЧЕТ СРЕДНЕЙ ПРОНИЦАЕМОСТИ ПЛАСТА ПРИ ЛИНЕЙНОЙ ФИЛЬТРАЦИИ ДЛЯ ИЗОЛИРОВАННЫХ ЗОН
РАСЧЕТ СРЕДНЕЙ ПРОНИЦАЕМОСТИ ПЛАСТА ПРИ ГОРИЗОНТАЛЬНО-ЛИНЕЙНОЙ ФИЛЬТРАЦИИ ДЛЯ ИЗОЛИРОВАННЫХ ЗОН
УДЕЛЬНАЯ ПОВЕРХНОСТЬ ГОРНЫХ ПОРОД
РАСПРЕДЕЛЕНИЕ НЕФТИ И ВОДЫ В НЕФТЯНЫХ ЗАЛЕЖАХ
ТЕРМИЧЕСКИЕ СВОЙСТВА ГОРНЫХ ПОРОД
ПОСТРОЕНИЕ ПАСПОРТА ПРОЧНОСТИ ГОРНОЙ ПОРОДЫ ПО МЕТОДУ КРУГОВ МОРА
абсцисс откладывают не диаметры частиц, а их логарифмы или величины, пропорциональные логарифмам.
Шкала называется логарифмической, если на ней нанесены логарифмы чисел, а отметками шкалы являются сами числа. Рисунок 10.

Рис. 10 логарифмическая шкала х рядом с равномерной шкалой у, на которой нанесены десятичные логарифмы чисел х
Равномерность шкалы у означает, что длина отрезка [у1, у2] между любыми двумя точками у1 и у2 этой шкалы пропорциональна разности у2 - у1 В частности, последовательные целые точки, y = 0, 1, 2, ... находятся на равных расстояниях друг от друга. На шкале х: против точек у = 0, 1, 2, 3... ставятся отметки х = 1, 10, 100... так что логарифмическая шкала х оказывается уже неравномерной. Промежуточные отметки шкалы х могут быть нанесены с помощью таблицы десятичных логарифмов, например, отметки х = 2; 3; 4; 5 наносятся против значений у = 0,301; 0,478; 0,602; 0,699. Очевидно, что точки х = 1, 2, 3, 4, 5, ... будут при этом находиться на неравных расстояниях. Логарифмическая шкала простирается неограниченно в обе стороны. Слева от точки х=1 находятся положительные числа, меньшие 1, десятичные логарифмы которых отрицательны.
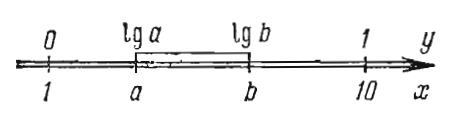
Рис. 11 соотношение чисел на логарифмической шкале
Для того чтобы нанести на шкалу какое-либо значение, необходимо задаться длинной единичного отрезка lg10 и воспользоваться правилом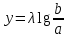 , где λ – масштабный коэффициент равный длине единичного отрезка.
, где λ – масштабный коэффициент равный длине единичного отрезка.
Используя кривую суммарного гранулометрического состава, вычисляют коэффициент неоднородности гранулометрического состава коллектора по формуле
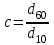 (18),
(18),
где: d60 - это диаметр частиц, при котором сумма масс фракций диаметрами, начиная от нуля и кончая данным диаметром, составляет 60% от массы всех фракций;
d10 - это диаметр частиц, при котором сумма масс фракций диаметрами, начиная от нуля и кончая данным диаметром, составляет 10% от массы всех фракций.
Коэффициент неоднородности пород нефтяных месторождений России колеблется в пределах 1,1...20.
Частицы коллектора, прошедшие через сито с наименьшими отверстиями, отбираются для седиментационного анализа. Седиментационный анализ основан на законе Стокса, т.е. седиментационном разделении частиц породы по фракциям вследствие различий скоростей оседания зерен неодинакового размера и плотности в вязкой жидкости.
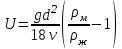 (19),
(19),
где: g - ускорение силы тяжести, м/с2; d - диаметр частиц; м; v – кинематическая вязкость жидкости, м2/с; ρж- плотность жидкости, кг/м3; ρм-плотность частиц, кг/м3.
Задача 6. В таблице представлены данные по гранулометрическому составу. Необходимо построить кривую суммарного гранулометрического состава и кривую распределения зерен по размерам. Найти коэффициент неоднородности.
Таблица 4
Исходные данные для задачи 6
Удельная поверхность пород - суммарная поверхность частиц или поровых каналов, содержащихся в единице объема образца, - зависит от степени дисперсности частиц, из которых они слагаются. Вследствие небольших размеров отдельных зерен песка и большой плотности их укладки поверхность порового пространства пласта может достигать огромных размеров, что значительно осложняет задачу полного извлечения! нефти из породы. Проницаемость, адсорбционная способность, содержание остаточной (реликтовой) воды и т.д. зависят от удельной поверхности нефтеносных пород.
Из-за небольших размеров частиц, слагающих горные породы, и большой плотности их упаковки общая площадь поверхностей порового пространства горной породы достигает огромных размеров.
От величины удельной поверхности нефтесодержащих пород зависят их проницаемость, содержание остаточной (связанной) воды, адсорбционная способность и так далее. Если пористая среда имеет большую удельную поверхность, то число поверхностных молекул жидкости возрастает и становится сравнимым с числом объемных молекул. Поэтому поверхностно-молекулярные явления в малопроницаемой породе могут оказать существенное влияние на процесс фильтрации жидкости, чем в высокопроницаемых горных породах.
Удельная поверхность нефтесодержащих горных пород нефтяных месторождений колеблется в больших пределах -от 40000 до 230000 м2/м3. Горные породы, имеющие удельную поверхность 230000 м2/м3 и более, относятся к слабопроницаемым. Это глины, глинистые пески, глинистые сланцы и тому подобное.
Удельную площадь поверхности фильтрации нефтесодержащих горных пород подсчитывают по приближенной формуле:
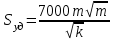 (20)
(20)
Sуд - удельная поверхность породы, м2/м3; m - пористость, доли единицы; k - проницаемость, м2
Иногда для удобства расчётов пользуются различными моделями
, упрощающими реальные процессы. Так для определения удельной поверхности и пористости породы часто используют понятие фиктивного грунта. Фиктивным принято называть воображаемый грунт, состоящий из воображаемых частиц одного и того же размера.
Из рисунка 12 видно, что каждый элемент фиктивного грунта, сложенный восемью шарообразными частицами, может иметь плотную и свободную укладку. При этом угол, α ромба, образованного линиями, соединяющими центры шаров, изменяется от 60 до 90°.
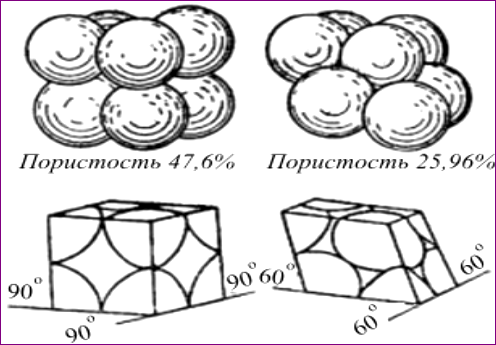
Рис. 12. Фиктивный грунт
Из геометрических соображений вытекает, что пористость фиктивного грунта в зависимости от угла α будет равна:
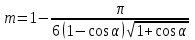 (21),
(21),
Число песчинок фиктивного грунта в единице объема может быть вычислено по формуле:
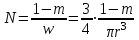 (22),
(22),
где w – объем одной песчинки, r – радиус песчинки
Суммарная поверхность всех песчинок в единице породы может быть найдена по формуле:
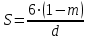 (23)
(23)
Для естественных грунтов удельная поверхность вычисляется суммированием ее значения по каждой фракции гранулометрического состава:
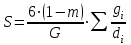 (24)
(24)
где G - масса породы, кг; gi, - масса данной фракции, кг; di - средние диаметры фракций (в м)
Можно свести формулу (24) к формуле (23) если ввести понятие эффективного диаметра, который рассчитывается по формуле:
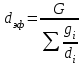 (25)
(25)
Задача 7 Рассчитайте пористость и удельную поверхность фиктивного грунта для крайних случаев угла α. Радиус песчинок примите последовательно: 1 мм; 0,5 мм и 0,1 мм. А также рассчитайте число песчинок в 1 м3
Задача 8 По результатам гранулометрического анализа рассчитайте значение удельной поверхности и эффективного диаметра. Диаметры даны в миллиметрах, масса навески в граммах.
Таблица 5
Исходные данные для задачи 8
Шкала называется логарифмической, если на ней нанесены логарифмы чисел, а отметками шкалы являются сами числа. Рисунок 10.

Рис. 10 логарифмическая шкала х рядом с равномерной шкалой у, на которой нанесены десятичные логарифмы чисел х
Равномерность шкалы у означает, что длина отрезка [у1, у2] между любыми двумя точками у1 и у2 этой шкалы пропорциональна разности у2 - у1 В частности, последовательные целые точки, y = 0, 1, 2, ... находятся на равных расстояниях друг от друга. На шкале х: против точек у = 0, 1, 2, 3... ставятся отметки х = 1, 10, 100... так что логарифмическая шкала х оказывается уже неравномерной. Промежуточные отметки шкалы х могут быть нанесены с помощью таблицы десятичных логарифмов, например, отметки х = 2; 3; 4; 5 наносятся против значений у = 0,301; 0,478; 0,602; 0,699. Очевидно, что точки х = 1, 2, 3, 4, 5, ... будут при этом находиться на неравных расстояниях. Логарифмическая шкала простирается неограниченно в обе стороны. Слева от точки х=1 находятся положительные числа, меньшие 1, десятичные логарифмы которых отрицательны.

Рис. 11 соотношение чисел на логарифмической шкале
Для того чтобы нанести на шкалу какое-либо значение, необходимо задаться длинной единичного отрезка lg10 и воспользоваться правилом
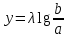 , где λ – масштабный коэффициент равный длине единичного отрезка.
, где λ – масштабный коэффициент равный длине единичного отрезка.Используя кривую суммарного гранулометрического состава, вычисляют коэффициент неоднородности гранулометрического состава коллектора по формуле
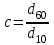 (18),
(18),где: d60 - это диаметр частиц, при котором сумма масс фракций диаметрами, начиная от нуля и кончая данным диаметром, составляет 60% от массы всех фракций;
d10 - это диаметр частиц, при котором сумма масс фракций диаметрами, начиная от нуля и кончая данным диаметром, составляет 10% от массы всех фракций.
Коэффициент неоднородности пород нефтяных месторождений России колеблется в пределах 1,1...20.
Частицы коллектора, прошедшие через сито с наименьшими отверстиями, отбираются для седиментационного анализа. Седиментационный анализ основан на законе Стокса, т.е. седиментационном разделении частиц породы по фракциям вследствие различий скоростей оседания зерен неодинакового размера и плотности в вязкой жидкости.
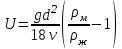 (19),
(19),где: g - ускорение силы тяжести, м/с2; d - диаметр частиц; м; v – кинематическая вязкость жидкости, м2/с; ρж- плотность жидкости, кг/м3; ρм-плотность частиц, кг/м3.
Задача 6. В таблице представлены данные по гранулометрическому составу. Необходимо построить кривую суммарного гранулометрического состава и кривую распределения зерен по размерам. Найти коэффициент неоднородности.
Таблица 4
Исходные данные для задачи 6
| № | Размер фракций, мм | | ||||||||||||
| 0,8 | 0,5 | 0,32 | 0,25 | 0,2 | 0,16 | 0,125 | 0,1 | 0,08 | 0,05 | 0,03 | 0,01 | 0,001 | ||
| Содержание фракций, нарастающий процент | | |||||||||||||
| 1 | | | | | 6 | 14 | 30 | 47 | 60 | 70 | 74 | 79 | 100 | |
| 2 | | | | | 5 | 12 | 25 | 45 | 60 | 70 | 76 | 82 | 100 | |
| 3 | | | | | | 7 | 21 | 37 | 48 | 58 | 61 | 71 | 100 | |
| 4 | | | | | | 7 | 23 | 41 | 63 | 77 | 85 | 90 | 100 | |
| 5 | | | | | | | 7 | 19 | 41 | 55 | 61 | 70 | 100 | |
| 6 | | | | 7 | 19 | 34 | 49 | 60 | 68 | 72 | 74 | 80 | 100 | |
| 7 | | | | 6 | 17 | 30 | 46 | 60 | 71 | 76 | 80 | 84 | 100 | |
| 8 | | | 5 | 12 | 21 | 35 | 52 | 68 | 78 | 85 | 89 | 92 | 100 | |
| 9 | | 6 | 14 | 24 | 40 | 59 | 71 | 82 | 87 | 90 | 93 | 95 | 100 | |
| 10 | 2 | 9 | 19 | 32 | 50 | 60 | 68 | 77 | 84 | 88 | 92 | 95 | 100 | |
| 11 | | 5 | 16 | 28 | 49 | 56 | 67 | 74 | 80 | 88 | 93 | 96 | 100 | |
| 12 | 1 | 3 | 11 | 23 | 44 | 51 | 59 | 66 | 72 | 81 | 86 | 91 | 100 | |
| 13 | | | | 5 | 17 | 29 | 47 | 62 | 69 | 78 | 83 | 88 | 100 | |
| 14 | | | 7 | 14 | 24 | 31 | 42 | 53 | 61 | 72 | 80 | 91 | 100 | |
| 15 | | 4 | 8 | 12 | 19 | 25 | 33 | 44 | 59 | 67 | 74 | 78 | 100 | |
УДЕЛЬНАЯ ПОВЕРХНОСТЬ ГОРНЫХ ПОРОД
Удельная поверхность пород - суммарная поверхность частиц или поровых каналов, содержащихся в единице объема образца, - зависит от степени дисперсности частиц, из которых они слагаются. Вследствие небольших размеров отдельных зерен песка и большой плотности их укладки поверхность порового пространства пласта может достигать огромных размеров, что значительно осложняет задачу полного извлечения! нефти из породы. Проницаемость, адсорбционная способность, содержание остаточной (реликтовой) воды и т.д. зависят от удельной поверхности нефтеносных пород.
Из-за небольших размеров частиц, слагающих горные породы, и большой плотности их упаковки общая площадь поверхностей порового пространства горной породы достигает огромных размеров.
От величины удельной поверхности нефтесодержащих пород зависят их проницаемость, содержание остаточной (связанной) воды, адсорбционная способность и так далее. Если пористая среда имеет большую удельную поверхность, то число поверхностных молекул жидкости возрастает и становится сравнимым с числом объемных молекул. Поэтому поверхностно-молекулярные явления в малопроницаемой породе могут оказать существенное влияние на процесс фильтрации жидкости, чем в высокопроницаемых горных породах.
Удельная поверхность нефтесодержащих горных пород нефтяных месторождений колеблется в больших пределах -от 40000 до 230000 м2/м3. Горные породы, имеющие удельную поверхность 230000 м2/м3 и более, относятся к слабопроницаемым. Это глины, глинистые пески, глинистые сланцы и тому подобное.
Удельную площадь поверхности фильтрации нефтесодержащих горных пород подсчитывают по приближенной формуле:
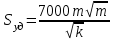 (20)
(20)Sуд - удельная поверхность породы, м2/м3; m - пористость, доли единицы; k - проницаемость, м2
Иногда для удобства расчётов пользуются различными моделями
, упрощающими реальные процессы. Так для определения удельной поверхности и пористости породы часто используют понятие фиктивного грунта. Фиктивным принято называть воображаемый грунт, состоящий из воображаемых частиц одного и того же размера.
Из рисунка 12 видно, что каждый элемент фиктивного грунта, сложенный восемью шарообразными частицами, может иметь плотную и свободную укладку. При этом угол, α ромба, образованного линиями, соединяющими центры шаров, изменяется от 60 до 90°.

Рис. 12. Фиктивный грунт
Из геометрических соображений вытекает, что пористость фиктивного грунта в зависимости от угла α будет равна:
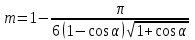 (21),
(21),Число песчинок фиктивного грунта в единице объема может быть вычислено по формуле:
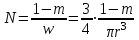 (22),
(22), где w – объем одной песчинки, r – радиус песчинки
Суммарная поверхность всех песчинок в единице породы может быть найдена по формуле:
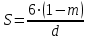 (23)
(23)Для естественных грунтов удельная поверхность вычисляется суммированием ее значения по каждой фракции гранулометрического состава:
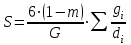 (24)
(24)где G - масса породы, кг; gi, - масса данной фракции, кг; di - средние диаметры фракций (в м)
Можно свести формулу (24) к формуле (23) если ввести понятие эффективного диаметра, который рассчитывается по формуле:
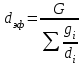 (25)
(25)Задача 7 Рассчитайте пористость и удельную поверхность фиктивного грунта для крайних случаев угла α. Радиус песчинок примите последовательно: 1 мм; 0,5 мм и 0,1 мм. А также рассчитайте число песчинок в 1 м3
Задача 8 По результатам гранулометрического анализа рассчитайте значение удельной поверхности и эффективного диаметра. Диаметры даны в миллиметрах, масса навески в граммах.
Таблица 5
Исходные данные для задачи 8
| № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| d1 | 0,06 | 0,11 | 0,1 | 0,09 | 0,04 | 0,09 | 0,12 | 0,08 | 0,09 | 0,1 |
| d2 | 0,12 | 0,18 | 0,16 | 0,13 | 0,14 | 0,17 | 0,16 | 0,17 | 0,15 | 0,16 |
| d3 | 0,16 | 0,22 | 0,3 | 0,27 | 0,24 | 0,23 | 0,29 | 0,27 | 0,22 | 0,25 |
| d4 | 0,24 | 0,38 | 0,34 | 0,29 | 0,26 | 0,35 | 0,36 | 0,38 | 0,39 | 0,34 |
| d5 | 0,34 | 0,41 | 0,38 | 0,39 | 0,34 | 0,46 | 0,49 | 0,44 | 0,4 | 0,42 |
| d6 | 0,4 | 0,44 | 0,42 | 0,41 | 0,38 | 0,48 | 0,56 | 0,66 | 0,54 | 0,58 |