Файл: Методические указания к практическим работам для студентов направления 21. 03. 01.docx

---

ПРОНИЦАЕМОСТЬ

Проницаемость – способность горной породы пропускать через себя флюид (воду, нефть или газ) при перепаде давления. Проницаемость бывает абсолютная, фазовая и относительная.

Абсолютная проницаемость – это проницаемость, определенная при наличии в среде только одной фазы, химически инертной к данной породе. Абсолютная проницаемость не зависит от свойств жидкости или газа, а также перепада давления – это свойство породы. Поскольку жидкости так или иначе реагируют с породой, на практике абсолютную проницаемость определяют по газу, как правило по воздуху или азоту.

Фазовая проницаемость – это проницаемость, определенная для данного флюида при наличии в породе других фаз. Значение фазовой проницаемости зависит не только от физических свойств пород, но и от насыщенности пор различными фазами, а также от физико-химических свойств этих фаз.

Относительная проницаемость – это отношение фазовой проницаемости к абсолютной.

Численное значение проницаемости обычно находят из закона линейной фильтрации Дарси. Согласно которому, скорость фильтрации жидкости в пористой среде может быть найдена исходя из следующего выражения:



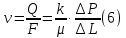
где v – скорость линейной фильтрации, м/с; Q – объемный расход жидкости в единицу времени, м³/с; η – динамическая вязкость жидкости, Па·с; F – площадь фильтрации, м²; ΔР – перепад давления, Па; L – длина пористой среды, м.

Коэффициент k – в данном выражении – это коэффициент пропорциональности, который носит название коэффициента проницаемости. Выразив k из выражения (6) получаем:



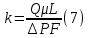
Единица измерения коэффициента проницаемости – м², однако на практике гораздо чаще встречается внесистемная единица измерения – Дарси (Д). 1 Д – 10^-12 м² или 1 мкм². Физический смысл размерности k – отражает то, что коэффициент проницаемости характеризует площадь каналов пористой среды, по которым происходит фильтрация. Как правило проницаемость коллекторов нефти и газа изменяется в пределах от нескольких мД (10

---

^-15 м²) до нескольких Д.

Формула (7) работает для линейной фильтрации жидкости, в случае линейной фильтрации газа, объемный расход должен быть заменен средний объемный расход, так как газ в отличии от жидкости расширяется при изменении давления, поэтому:



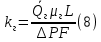
где 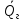– объемный расход газа приведенный к среднему давлению и средней температуре газа на пути L в пористой среде.

На практике объемный расход газа приведенный к среднему давлению и средней температуре газа определить затруднительно, поэтому формула (8) не используется. Для того чтобы заменить 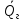в выражении (8) проводят несколько простых манипуляций:

Из закона Бойля-Мариотта для изотермического течения идеального газа имеем:





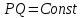
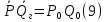
где P₀ и Q₀ – атмосферное давление и расход газа при атмосферном давлении соответственно.

Среднее давление в керне находим по формуле



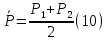
А объемный расход газа, приведенный к среднему давлению и средней температуре газа выражаем из уравнения (9)



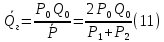
В результате несложных преобразований получаем выражения для расчета линейной фильтрации газа в пористой среде:



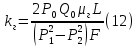
Иногда возникает необходимость определить проницаемость образцов при радиальной фильтрации жидкости или газа, как бы воспроизвести условия их притока в скважину. В данном случае образец породы подготавливают к опыту в виде цилиндрического кольца с осевым отверстием –«скважиной», а фильтрация идет через боковую поверхность образца в радиальном направлении. В этом случае проницаемость породы при фильтрации жидкости определяют по формуле:

---

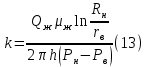
Для газа по формуле:



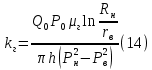
Задача 2. Необходимо рассчитать проницаемость керна диметром d и длинной l по нефти, давление на входе в образец Р₁ мм рт.ст., а давление на выходе Р₂ мм рт.ст. За время исследования t сек, в градуированный цилиндр отфильтровался объем V мл. Динамическая вязкость нефти μ мПа·с.

Таблица 2

Исходные данные для задачи 2

№	d, см	l, см	P1, мм.рт.ст	Р2, мм.рт.ст	t, сек	V, мл	μ, мПа·с
1	4,15	2,5	1000	760	300	31	14
2	4,2	2,6	1100	760	300	52	10
3	4,25	2,7	1200	760	300	27	2
4	4,3	2,8	1100	760	300	40	5
5	4,35	2,9	1300	760	300	92	3

продолжение таблицы 2

№	d, см	l, см	P1, мм.рт.ст	Р2, мм.рт.ст	t, сек	V, мл	μ, мПа·с
6	4,4	3	1200	760	300	45	77
7	4,45	3,1	1300	760	300	88	6
8	4,5	3,2	960	760	300	87	8
9	4,55	3,3	950	760	300	35	92
10	4,6	3,4	970	760	300	95	19
11	4,65	3,5	980	760	300	99	32
12	4,7	3,6	990	760	300	100	44
13	4,75	3,7	950	760	300	99	48
14	4,8	3,8	945	760	300	96	49
15	4,85	3,9	960	760	300	48	20
16	4,9	4	950	760	300	44	63
17	4,95	4,1	970	760	300	59	38
18	5	4,2	980	760	300	90	39
19	4,15	4,3	990	760	300	25	46
20	4,2	4,4	950	760	300	42	43
21	4,25	4,5	945	760	300	10	9
22	4,3	4,6	960	760	300	39	1
23	4,35	4,7	950	760	300	47	0,1
24	4,4	4,8	970	760	300	54	12
25	4,45	4,9	980	760	300	45	0,8

---

Задача 3. На рисунке 1 изображена зависимость относительных проницаемостей по нефти и по воде от насыщенности порового пространства водой. Определите значение относительной проницаемости для смеси нефти и воды в образце песка, коэффициент водонасыщенности которого составляет 20%, 30%, 40%, 50% и 60%.



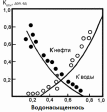
Рис.1. Зависимость относительных проницаемостей по нефти и по воде от насыщенности порового пространства водой
Задача 4. На рисунке 2 изображена тройная диаграмма насыщенности при трехфазной фильтрации. Опишите три различных случая фильтрации потока при нефтенасыщенности 20%. Опишите четыре различных случая фильтрации потока при нефтенасыщенности 40 %. Опишите четыре различных случая фильтрации потока при водонасыщенности 40 %.


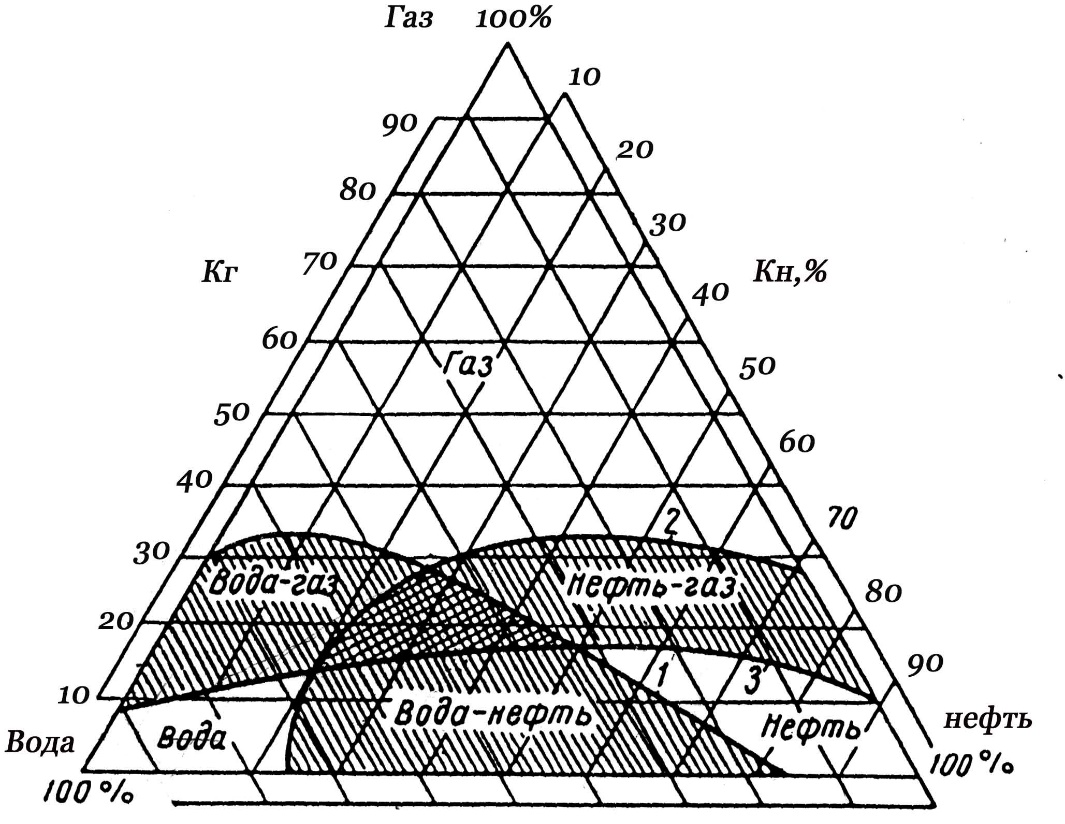
Рис. 2 Тройная диаграмма насыщенности для фильтрации трёхфазной системы нефть-газ-вода.

---