Файл: Законы сохраненияЛекция.doc

Рдиус-вектор r_c (t) определяет положение точки, назы­ваемой центром инерции системы (точка С на рис. 1). На рис. 1, что векторы , , , , можно считать приложенными к центру инерции С. Это осу­ществляется параллельным переносом векторов , , , из точек своего приложения (1) и (2) в точку С, как показано пунктирными стрелками на рис. 1, а затем суммированием , и , соответственно.

Обобщение изложенного на случай системы, состоя­щей из п частиц, приводит к определению радиуса-вектора центра инерции системы:

(13).

Движение центра инерции определяется уравнением движения в дифференциальном виде (12). Можно ска­зать поэтому, что центр инерции системы движется так, как двигалась бы частица с массой, равной сум­марной массе системы, под действием силы, равной суммарной внешней силе. Продифференцировав (13) по времени, найдем скорость центра инерции:

Из этого выражения следует, что скорость центра инер­ции определяется полным импульсом системы. Из этого, а также из (5), (12) вытекает, что движение центра инерции можно отождествлять с поступательным дви­жением системы как целого, выделяя последнее тем самым из общего движения системы.

В случае, если система замкнута, то из (5) следует закон сохранения импульса и тогда из соотношения v_c = р_с/т вытекает закон сохранения скорости центра инерции: центр инерции замкнутой системы тел движется равномерно и прямолинейно или нахо­дится в состоянии покоя. Этот закон является обобщением на системы частиц закона инерции, т. е. первого закона Ньютона.

---

Обратим внимание на то, что импульс центра инерции связан со скоростью центра инерции (р_с = mv_c) так же как импульс и скорость одной частицы. При этом коэффициент пропорциональности между импульсом и скоростью центра инерции равен сумме масс отдельных частиц, и, очевидно, имеет смысл массы всей системы. В этом выражается закон аддитивности массы.

Коснемся способа измерения инертной массы тел. Покажем, что с помощью за­кона сохранения импульса можно определить массы частиц, если массу одной из них принять за эталон­ную.

Припишем частице-эталону массу m₀, что будет соот­ветствовать выбору системы единиц. Для нахождения массы т другой частицы рассмотрим процесс столкновения этой частицы с эталоном. Детальным ходом процесса столкновения можно не интересоваться. Будем только считать, что массы частиц при столкновении не измени­лись, и что в начальном и конечном состояниях частицы находятся достаточно далеко друг от друга, чтобы каж­дую из них можно было считать свободной. Пусть v₀ и v — скорости эталонной и исследуемой частиц до столк­новения, a v₀’ и v' — их скорости после столкновения. Из закона сохранения импульса системы частиц (которая, очевидно, замкнута) следует , от­куда получаем . Таким образом, измерив скорости частиц до и после, их упругого соударения, мы можем определить массу исследуемой частицы m через массу эталонной частицы m₀.

---

П.2 Закон сохранения момента импульса.

При описании вращательного движения важнейшими динамическими характеристиками являются момент силы М и момент импульса L. Момент силы характе­ризует в динамике ее способность вызывать вращение тел и изменять угловую скорость. Различают момент силы относительно центра (точки) и относительно оси.

Моментом силы относительно центра «о» называется векторная величина , где — радиус-вектор точки приложения силы, проведенный из центра.

М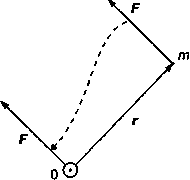омент импульса во вращательном движении иг­рает ту же роль, что и импульс в поступательном движении.

Различают момент импульса относительно оси и относительно центра (точки). Момент импульса относительно центра «О» равен .

Определение момента силы и момента импульса относительно оси будет дано в гл. 1.6.

Получим теперь закон сохранения момента импуль­са. Это фундаментальный закон физики. Его фунда­ментальность обусловлена тем, что он непосредственно связан со свойством изотропности пространства и при­меним не только в классической механике, но и в дру­гих разделах физики. В классической механике закон сохранения момента импульса может быть выведен на основе законов Ньютона. Ограничимся рассмотрением системы, состоящей из двух частиц, а затем обобщим результаты на системы из произвольного числа частиц.

Запишем для двух точек уравнения, вытекающие из законов Ньютона, (1), (2). Умножим векторно слева уравнение (1) на а уравнение (2) — на , сложим почленно получившиеся выражения:

(14)

Преобразуем левые части (14), учитывая, что:

(15)

где векторы и коллинеарны (параллельны одной и той же прямой), а их векторное произведение равно нулю. Первые два слагаемых справа в (14) равны нулю, так как (16)

---

В (16) мы применили третий закон Ньютона для внутренних сил, а также тот факт, что вектор лежит на прямой, соединяющей точки 1 и 2, а значит, коллинеарен вектору f₁₂ (см. рис. 1), что и приводит к равенству нулю суммарного момента внут­ренних сил (16). Учитывая (15), (16), из (14) получим:

или

(17) - Называется уравнением моментов.

Здесь - суммарный момент импульса системы и - суммарный момент внешних сил, дейст­вующих на систему. Согласно первому из равенств, момент импульса системы частиц, также как и импульс системы, является аддитивной величиной. Обобщая полученный результат на систему из п частиц, мы можем записать: . Соотношение (17) справедливо и для системы из N частиц.

Если система замкнута, то М = 0 и из (17) следует:

, , (18)

Для замкнутой системы справедлив закон сохранения момента импульса: суммарный момент импульса зам­кнутой системы тел сохраняется.

Также как и в случае импульса системы и здесь возможны ситуации, когда существуют такие направ­ления в пространстве, что проекция суммарного момента внешних сил на них равна нулю. В этом случае будет сохраняться не весь суммарный момент импульса сис­темы, а только его проекции на эти направления: , , (19).

В отношении закона сохранения момента импульса в классической форме (т. е. в той, в какой он сформулиро­ван в данном пункте) справедливы те же замечания по его выполнимости, что и в отношении закона сохране­ния импульса (см. предыдущий пункт).

Отметим также следующее. Момент импульса сис­темы, определенный относительно центра инерции, на­зывается собственным моментом импульса системы. Это понятие, соответствующим образом видоизмененное, имеет большое значение в области микромира.

---

---