ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 01.08.2024
Просмотров: 174
Скачиваний: 0
СОДЕРЖАНИЕ
Тема 10 статистическое изучение динамики социально-экономических явлений
Понятие и классификация рядов динамики
10.2 Сопоставимость уровней и смыкание рядов динамики
10.3 Аналитические показателиизменения уровней ряда динамики
10.5 Виды трендовой компоненты и проверка гипотезы о существовании тенденции
10.6 Методы анализа основной тенденции (тренда) в рядах динамики
10.7 Методы выявления периодической компоненты. Модели сезонных колебаний
10.8 Регрессионный анализ связных динамических рядов
Наличие последней приводит к искажению величин средних квадратических ошибок коэффициентов регрессии, что затрудняет построение доверительных интервалов для коэффициентов регрессии, а также проверку их значимости.
Автокорреляцию измеряют при помощи
нециклического коэффициента
автокорреляции, который может
рассчитываться не только между соседними
уровнями, т.е. сдвинутыми на один период,
но и между сдвинутыми на любое число
единиц времени (![]() ).
Этот сдвиг, именуемыйвременным лагом,
определяет и порядок коэффициентов
автокорреляции: первого порядка (при
).
Этот сдвиг, именуемыйвременным лагом,
определяет и порядок коэффициентов
автокорреляции: первого порядка (при![]() ),
второго порядка (при
),
второго порядка (при![]() )
и т.д. Однако наибольший интерес для
исследования представляет вычисление
нециклического коэффициента (первого
порядка), так как наиболее сильные
искажения результатов анализа возникают
при корреляции между исходными уровнями
ряда (
)
и т.д. Однако наибольший интерес для
исследования представляет вычисление
нециклического коэффициента (первого
порядка), так как наиболее сильные
искажения результатов анализа возникают
при корреляции между исходными уровнями
ряда (![]() )
и теми же уровнями, сдвинутыми на одну
единицу времени, т.е.
)
и теми же уровнями, сдвинутыми на одну
единицу времени, т.е.![]() (или
(или![]() ).
).
Тогда формулу коэффициента автокорреляции можно записать следующим образом:
|
|
(10.45) |
|
где |
|
|
Если значение последнего уровня (![]() )
ряда мало отличается от первого (
)
ряда мало отличается от первого (![]() ),
то сдвинутый ряд не укорачивается, его
можно условно дополнить, приняв
),
то сдвинутый ряд не укорачивается, его
можно условно дополнить, приняв![]() .
Тогда
.
Тогда![]() и
и![]() ,
поскольку рассчитываются они для одного
и того же ряда. При такой замене, т.е.
если
,
поскольку рассчитываются они для одного
и того же ряда. При такой замене, т.е.
если![]() и
и![]() формула коэффициента автокорреляции
примет вид:
формула коэффициента автокорреляции
примет вид:
|
|
(10.46) |
Если ряд динамики состоит из уровней,
среднее значение которых равно нулю
(![]() ),
то выражение (10.46) значительно упрощается:
),
то выражение (10.46) значительно упрощается:
|
|
(10.47) |
Для суждения о наличии или отсутствии автокорреляции в исследуемом ряду фактическое значение коэффициентов автокорреляции сопоставляется с табличным (критическим) для 5%-го или 1%-го уровня значимости (вероятность допустить ошибку при принятии нулевой гипотезы о независимости уровней ряда).
Одна из специальных таблиц, в которой определена критическая область проверяемой гипотезы (об отсутствии автокорреляции), составленная Р. Андерсеном в 1942 г., приведена в приложении 12.
Если фактическое значение коэффициента автокорреляции меньше табличного, то гипотеза об отсутствии автокорреляции в ряду может быть принята. Когда же фактическое значение больше табличного, можно сделать вывод о наличии автокорреляции в ряду динамики.
Способ выявления автокорреляции в отклонениях от тренда или от регрессионной модели. Таким способом является использованиекритерия Дарбина-Уотсона, который рассчитывается по формуле:
|
|
(10.48) |
|
где |
|
|
Теоретическое основание применения этого критерия обусловлено тем, что в динамических рядах как сами наблюдения, так и отклонения от них распределяются в хронологическом порядке.
При условии, что отклонения уровней от
тенденции (так называемые остатки)
случайны, значения
![]() ,
лежащие в интервале 0 - 4, всегда будут
находиться ближе к 2. Если автокорреляция
положительная, то
,
лежащие в интервале 0 - 4, всегда будут
находиться ближе к 2. Если автокорреляция
положительная, то![]() ;
отрицательная
;
отрицательная![]() .
Следовательно, оценки, получаемые по
критерию, являются не точечными, а
интервальными. Их значения для трех
уровней значимости (
.
Следовательно, оценки, получаемые по
критерию, являются не точечными, а
интервальными. Их значения для трех
уровней значимости (![]() ,
,![]() и
и![]() )
с учетом числа наблюдений даны в
специальных таблицах (см. приложение
14).
)
с учетом числа наблюдений даны в
специальных таблицах (см. приложение
14).
Способы исключения или уменьшения автокорреляции (авторегрессии) в рядах динамики.
К ним относятся:
метод включения времени в качестве дополнительного фактора;
метод последовательных разностей;
метод авторегрессионных преобразований.
Рассмотрим эти способы. В соответствии с теоремой, доказанной Фришем и Воу, время вводится в систему связных динамических рядов в явной форме в качестве дополнительного фактора, и эта процедура называется введением фактора времени в уравнение регрессии. Уровни исходных динамических рядов могут быть представлены показателями в любой форме, в том числе логарифмической, а время всегда вводится в линейной форме. Считается, что введение фактора времени исключает основную тенденцию развития всех явлений, представленных исследуемыми рядами динамики. Доказано, что введение времени аналогично использованию отклонения фактических данных от трендов.
Применение метода наименьших квадратов к обработке многомерных временных рядов не отличается от методологии применения его к обычным статистическим рядам. В рассматриваемом случае минимизируется следующее выражение:
![]() .
.
При исключении автокорреляции методом
последовательных разностей подвергаются
обработке методом наименьших квадратов
не сами уровни исходных рядов![]() и
и![]() а последовательные разности между
ними:
а последовательные разности между
ними:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При использовании этого метода исходят из предположения, что все разности между уровнями динамических рядов, начиная с первой, будут содержать только случайную компоненту. Причем первые разности содержат случайную компоненту в линейной форме, вторые - описываемую параболой 2-го порядка, третьи – показательной функцией.
Метод авторегрессионных преобразований заключается в том, что определяют уравнение связи между отклонениями от тенденций двух связных рядов динамики:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В этом случае также получают уравнения регрессии, не искаженные влиянием автокорреляции.
Введение времени в качестве дополнительной переменной является наиболее действенным способом обработки связных рядов динамики. Во всяком случае, при линейной связи между исследуемыми рядами этот способ более точен, чем использование последовательных разностей или отклонений от трендов.
При обработке методом наименьших квадратов последовательных разностей или отклонений от трендов исследователь имеет дело с чисто случайными величинами, взаимосвязь между которыми является часто весьма сомнительной, так как исключение в обоих случаях тенденций нарушает существование причинно-следственной связи между явлениями.
10.9 Корреляция рядов динамики
При изучении развития явления во времени часто возникает необходимость оценить степень взаимосвязи в изменениях уровней двух или более рядов динамики различного содержания, но связанных между собой.
Эта задача решается методами коррелирования:
уровней ряда динамики;
отклонений фактических уровней от тренда;
последовательных разностей, т.е. путем исчисления парного коэффициента корреляции.
Расчет парного коэффициента корреляции по уровням ряда динамики. Этот расчет правильно показывает тесноту связи между рядами динамики лишь в том случае, если в каждом из них отсутствует автокорреляция.
В этом случае величину коэффициента корреляции находят по формуле:
|
|
(10.49) |
|
где |
|
|
|
|
|
|
Следовательно, прежде чем коррелировать ряды динамики (по уровням), необходимо проверить каждый из рядов на наличие или отсутствие в них автокорреляции (при помощи коэффициента автокорреляции, описанного в разделе 10.8). В случае наличия автокорреляции между уровнями ряда последняя должна быть устранена.
Рассмотрим способы ее исключения в рядах динамики.
Расчет парного коэффициента корреляции
по отклонениям фактических уровней от
выравненных по уравнению (тренду). Этот
способ состоит в том, что коррелируют
не сами уровни, а отклонения фактических
уровней от выравненных, отражающих
тренд, т.е. коррелируют остаточные
величины. Для этого каждый ряд динамики
выравнивают по определенной, характерной
для него аналитической формуле, затем
из эмпирических уровней вычитают
выравненные (т.е. находят![]() ;
;![]() )
и определяют тесноту связи между
рассчитанными отклонениями (
)
и определяют тесноту связи между
рассчитанными отклонениями (![]() и
и![]() )
по формуле
)
по формуле
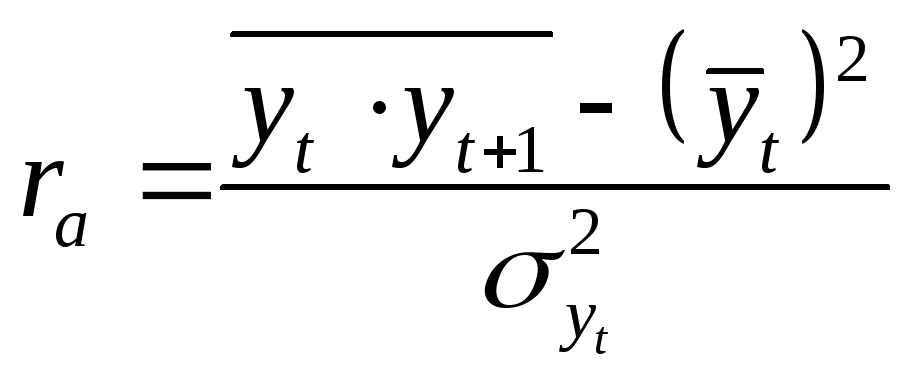 или
или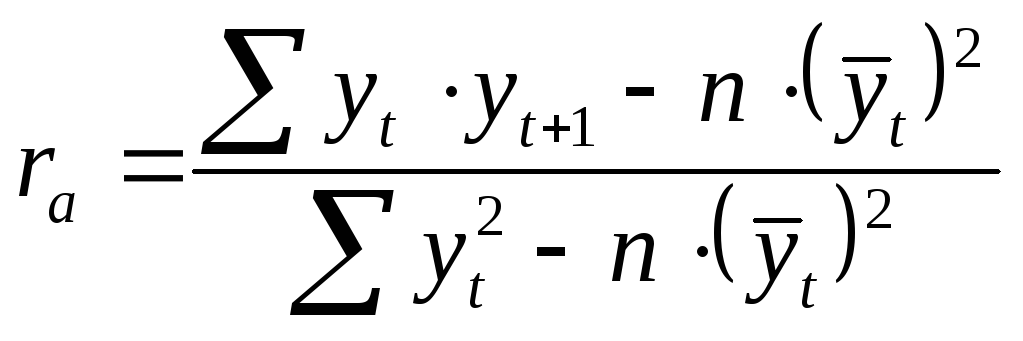 .
.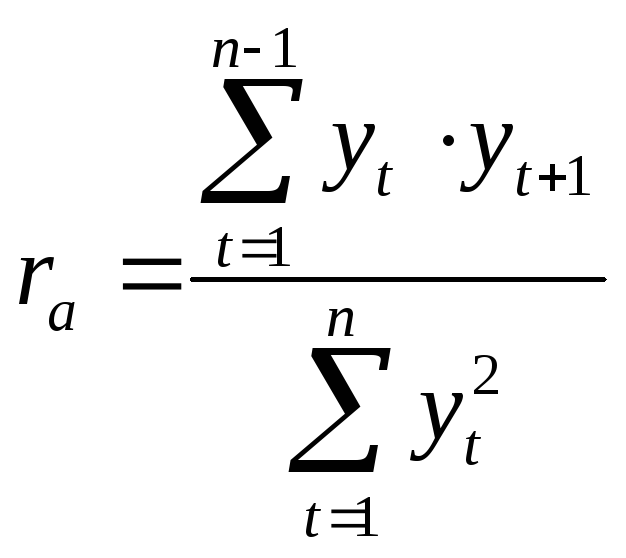 .
.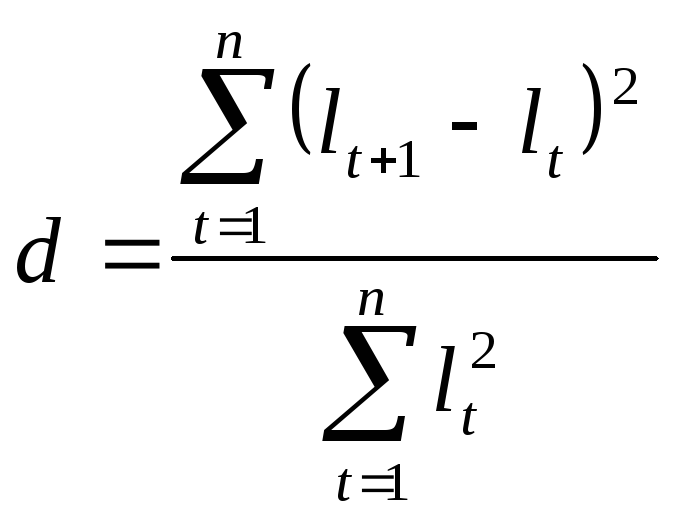 ,
,