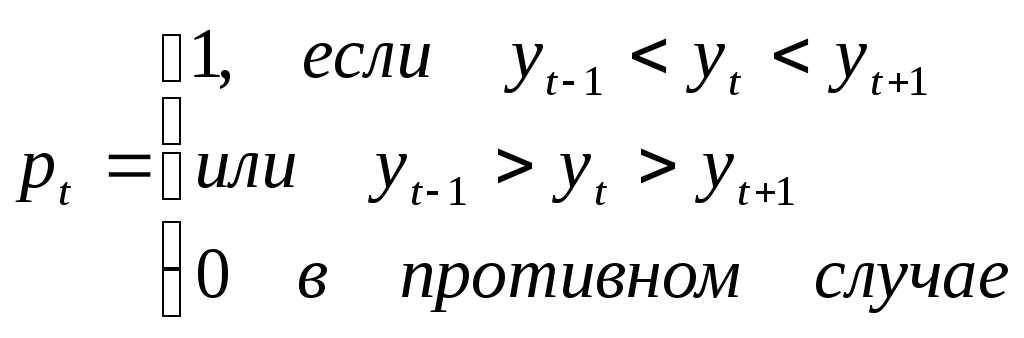Файл: Тема 10.doc

Для определенных в каждом конкретном случае находят значения синусов и косинусов разных гармоник, которые для удобства располагают в таблице10.3.

Таблица 10.3
Коэффициент гармонического анализа месячных наблюдений для расчета параметров и
0	1	1	1	1	0	0	0	0
	0,866	0,5	0	-0,5	0,5	0,866	1	0,866
	0,5	-0,5	-1	-0,5	0,866	0,866	0	-0,866
	0	-1	0	1	1	0	-1	0
	-0,5	-0,5	1	-0,5	0,866	-0,866	0	0,866
	-0,866	0,5	0	-0,5	0,5	-0,866	1	-0,866
	-1	1	-1	1	0	0	0	0
	-0,866	0,5	0	-0,5	-0,5	0,866	-1	0,866
	-0,5	-0,5	1	-0,5	-0,866	0,866	0	-0,866
	0	-1	0	1	-1	0	1	0
	0,5	-0,5	-1	-0,5	-0,866	-0,866	0	0,866
	0,866	0,5	0	-0,5	-0,5	-0,866	-1	-0,866

---

Полагая гармоники соответственно равными 1, 2, 3 и т.д., находим все значения и. Тогда, например, первая гармоника ряда Фурье примет вид:

,

здесь:

;;.

(10.39)

Ряд Фурье с двумя гармониками:

,

(10.40)

где

;.

Исчисление параметров ряда Фурье может производиться и другими способами, а также путем использования различных шаблонов.

Пример. Полагая наличие периодичности, проведем гармонический анализ динамики отклонений от линейной тенденции данных об урожайности ярового ячменя в одном из хозяйств на 1990-2001 гг. () (табл. 10.4). Проведем расчеты первой гармоники (для значений синусов и косинусов используем данные табл. 10.3).

Отсюда можно определить параметры:

;;.

Следовательно, 1-я гармоника описывается уравнением

.

Аналогично рассчитываются гармоники 2-го и высших порядков, и значения их последовательно присоединяются к значениям 1-й гармоники. Запишем уравнения искомых отклонений с 2-й и 3-й гармоник.

---

Для 2-й гармоники:

.

Для 3-й гармоники:

.

Подставив в уравнение конкретные значения ,,,,,, получим выравненные уровни отклонений урожайности ярового ячменя за 1990-2001 гг. Затем, рассчитав остаточные диспер­сии () для трех гармоник, можно сделать вывод, какая гармоника ряда Фурье наиболее близка к фактическим уровням ряда.

Таблица 10.4
Отклонения от линейной тенденции данных об урожайности ярового ячменя и расчет параметров и в модели сезонной волны
Год
1990	2,1	0	2,1	0	0,81	0	0,81
1991	-2,0		-1,732	-1,0	0,701	-0,212	0,49
1992	0,5		0,25	0,433	0,405	-0,366	0,04
1993	-0,1		0	0,1	0	-0,423	-0,423
1994	2,8		-1,4	2,425	-0,405	-0,366	-0,797
1995	-2,5		2,165	-1,25	-0,701	-0,212	-0,913
1996	-3,1		3,1	0	-0,81	0	-0,81
1997	-2,0		1,732	1,0	-0,701	0,121	-0,489
1998	3,4		-1,7	-2,944	-0,405	0,366	-0,04
1999	-0,6		0	0,6	0	0,423	0,423
2000	2,6		1,3	-2,252	0,405	0,366	0,771
2001	-1,1		-0,953	0,55	0,701	0,212	0,912
Итого	0,0	-	4,862	-2,538	-	-	0,0

---

---

10.7 Методы выявления периодической компоненты. Модели сезонных колебаний

Для проверки предположения о существенности периодической компоненты ряда динамики целесообразно использовать такие критерии случайности, которые имеют наибольшую мощность относительно альтернативной гипотезы о цикличности ряда. Наиболее простым для применения и зрительно понятным является критерий «пиков» и «ям». В основе этого критерия лежит подсчет числа экстремальных точек ряда , который осуществляется следующим образом:

,

где
	;

число наблюдений в ряду динамики.

Для случайного ряда математическое ожидание числа экстремальных точек

Проверка гипотезы сводится к сравнению с расчетным значением. Если эти значения близки, то можно отказаться от дальнейшей проверки и признать ряд случайным. Если же и значительно отличаются друг от друга, то проводится дальнейшая проверка гипотезы, основанная на подсчете фаз различной длины.

Фазой называется интервал между двумя соседними уровнями, для которых. Для определениядлины фазыдостаточно просто найти разности индексов двух соседних экстремальных точек, затем подсчитать число фаз,,длин,,. Теоретическое значение числа фаз длиныдля случайного ряда следующее:

---