Файл: Тема 10.doc

.

(10.41)

Естественная процедура проверки случайности сводится к сравнению наблюдаемых значений ,,с теоретическим значением. Однако при небольшом числе наблюдений критерийздесь непосредственно использовать нельзя, так как в этом случае длины фазне являются независимыми. Доказано, что при разбиении длины фазы на три группы:,,(две степени свободы) - статистикаможет быть использована в обычной форме () при. Расчетные значенияв случае трех групп длин фазы определяются по формуле

.

(10.42)

Если , то колебания исходного ряда нельзя считать чисто случайными и ряд содержит периодическую составляющую. Этот критерий весьма чувствителен к периодическим колебаниям и имеет практически нулевую эффективность относительно альтернативы наличия тренда, поэтому он может применяться непосредственно к исходному ряду динамики в отличие от других критериев, которые требуют, чтобы из ряда динамики предварительно была выделена систематическая составляющая. После того как установлена периодическая составляющая, проводится ее анализ.

---

При рассмотрении квартальных или месячных данных многих социально-экономических явлений часто обнаруживаются определенные, постоянно повторяющиеся колебания, которые существенно не изменяются за длительный период времени. Они являются результатом влияния природно-климатических условий, общих экономических факторов, а также ряда многочисленных разнообразных факторов, которые частично являются регулируемыми. В статистике периодические колебания, которые имеют определенный и постоянный период, равный годовому промежутку, носят название сезонных колебаний, илисезонных волн, а динамический ряд в этом случае называюттренд-сезонным, или простосезонным рядом динамики.

Сезонные колебания характеризуются специальными показателями, которые называются индексами сезонности (). Совокупность этих показателей отражает сезонную волну. Индексами сезонности являются процентные отношения фактических внутригодовых уровней к постоянной или переменной средней.

Для выявления сезонных колебаний обычно берут данные за несколько лет, распределенные по месяцам. Данные за несколько лет (не менее трех) используют для того, чтобы выявить устойчивую сезонную волну, которая бы не отражала случайные условия одного года.

Для вычисления индексов сезонности применяют различные методы. Если ряд динамики не содержит ярко выраженной тенденции в развитии, то индексы сезонности вычисляют непосредственно по эмпирическим данным без их предварительного выравнивания.

Для каждого месяца рассчитывается средняя величина уровня, например за три года (), затем из них вычисляется среднемесячный уровень для всего ряда () и в заключение определяется процентное отношение средних для каждого месяца к общему среднемесячному уровню ряда, т.е.

.

(10.43)

Для наглядного получения представления о сезонной волне желательно изобразить полученные данные в виде линейной диаграммы.

Если ряд динамики содержит определенную тенденцию в развитии, то прежде чем вычислить сезонную волну фактические данные нужно обработать так, чтобы выявить общую тенденцию. Обычно для этого прибегают к аналитическому выравниванию ряда динамики.

---

При использовании способа аналитического выравнивания алгоритм вычислений индексов сезонности следующий:

• по соответствующему полиному вычисляют для каждого месяца (квартала) выравненные уровни на момент времени ();

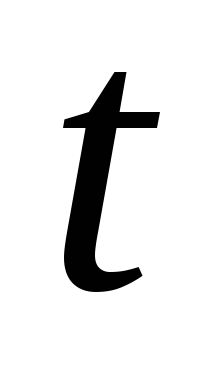• определяют отношения фактических месячных (квартальных) данных () к соответствующим выравненным данным (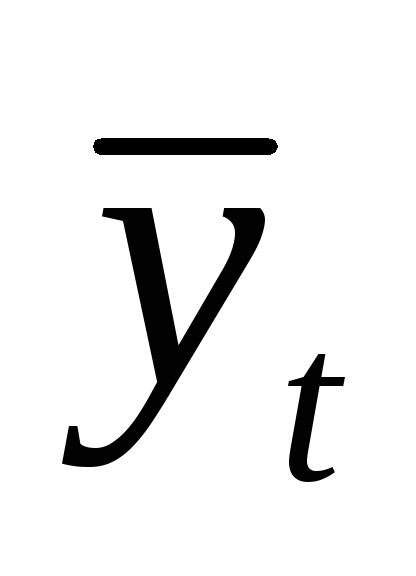) в процентах;

;

• находят средние арифметические из процентных соотношений, рассчитанных по одноименным периодам в процентах:

,

где

число одноименных периодов.

В общем виде формулу расчета индекса сезонности данным способом можно записать так:

.

(10.44)

В табл. 10.4 дана классификация наиболее распространенных методов измерения сезонной волны.

Таблица 10.4

Классификация методов измерения сезонной волны

Методы измерения сезонной волны, основанные на применении

Средней арифметической:

метод абсолютных разностей

метод отношений средних помесячных к средней за весь период

метод отношений помесячных уровней к средней данного года

Относительных величин:

метод относительных величин

метод относительных величин на основе медианы

метод У. Персонса (цепной метод)

Механического выравнивания:

метод скользящих средних

метод скользящих сумм и скользящих средних

Аналитического выравнивания:

выравнивание по прямой

выравнивание по параболе и экспоненте

выравнивание по ряду Фурье

---

---

10.8 Регрессионный анализ связных динамических рядов

Многомерные временные ряды, показывающие зависимость результативного признака от одного или нескольких факторных, называют связными рядами динамики. Применение методов наименьших квадратов для обработки рядов динамики не требует выдвижения никаких предположений о законах распределения исходных данных. Однако при использовании метода наименьших квадратов для обработки связных рядов следует учитывать наличие автокорреляции (авторегрессии), которая не учитывалась при обработке одномерных рядов динамики, поскольку ее наличие способствовало более плотному и четкому выявлению тенденции развития рассматриваемого социально-экономического явления во времени.

Выявление автокорреляции в уровнях ряда динамики. В рядах динамики экономических процессов между уровнями, особенно близко расположенными, существует взаимосвязь. Ее удобно представить в виде корреляционной зависимости между рядами,,, …,и этим же рядом, сдвинутым относительно первоначального положения намоментов времени,,, …,. Временное смещение называетсясдвигом, а само явление взаимосвязи -автокорреляцией.

Автокорреляционная зависимость особенно существенна между последующими и предшествующими уровнями ряда динамики. Поскольку классические методы математической статистики применимы лишь в случае независимости отдельных членов ряда между собой, то при анализе нескольких взаимосвязанных рядов динамики важно установить наличие и степень их автокорреляции. Различаются два вида автокорреляции:

• автокорреляция в наблюдениях за одной или более переменными;

• автокорреляция ошибок или автокорреляция в отклонениях от тренда.

---