ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 01.08.2024
Просмотров: 177
Скачиваний: 0
СОДЕРЖАНИЕ
Тема 10 статистическое изучение динамики социально-экономических явлений
Понятие и классификация рядов динамики
10.2 Сопоставимость уровней и смыкание рядов динамики
10.3 Аналитические показателиизменения уровней ряда динамики
10.5 Виды трендовой компоненты и проверка гипотезы о существовании тенденции
10.6 Методы анализа основной тенденции (тренда) в рядах динамики
10.7 Методы выявления периодической компоненты. Модели сезонных колебаний
10.8 Регрессионный анализ связных динамических рядов
|
|
(10.22) |
|
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определение скользящей средней по четному числу членов ряда динамики несколько сложнее, так как средняя может быть отнесена только к середине между двумя датами, находящимися в середине интервала сглаживания.
Если число членов скользящей средней
обозначить через
![]() ,
то серединным будет уровень, относящийся
к
,
то серединным будет уровень, относящийся
к![]() члену ряда, т.е. имеет место сдвиг периода,
к которому относится уровень. Например,
средняя, найденная для четырех членов,
относится к середине между вторым и
третьим периодами, следующая средняя
- к середине между третьим и четвертым
и т.д. Чтобы ликвидировать такой сдвиг,
применяют так называемыйспособ
центрирования. Центрирование
заключается в нахождении средней из
двух смежных скользящих средних для
отнесения полученного уровня к
определенной дате. При центрировании
необходимо находить скользящие суммы,
скользящие средние нецентрированные
по этим суммам и средние из двух смежных
нецентрированных скользящих средних.
члену ряда, т.е. имеет место сдвиг периода,
к которому относится уровень. Например,
средняя, найденная для четырех членов,
относится к середине между вторым и
третьим периодами, следующая средняя
- к середине между третьим и четвертым
и т.д. Чтобы ликвидировать такой сдвиг,
применяют так называемыйспособ
центрирования. Центрирование
заключается в нахождении средней из
двух смежных скользящих средних для
отнесения полученного уровня к
определенной дате. При центрировании
необходимо находить скользящие суммы,
скользящие средние нецентрированные
по этим суммам и средние из двух смежных
нецентрированных скользящих средних.
Сдвинуть интервал сглаживания на одну точку вправо, потом вычислить по формуле (10.22) сглаженное значение для
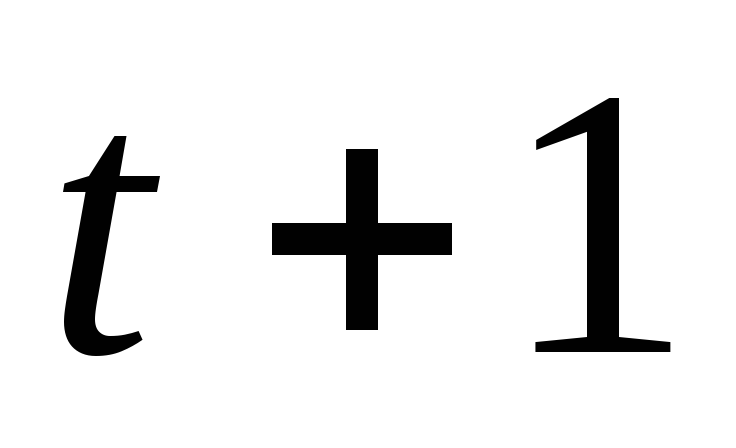 члена, снова произвести сдвиг и т.д. В
результате последовательного применения
приведенной итеративной процедуры
получится
члена, снова произвести сдвиг и т.д. В
результате последовательного применения
приведенной итеративной процедуры
получится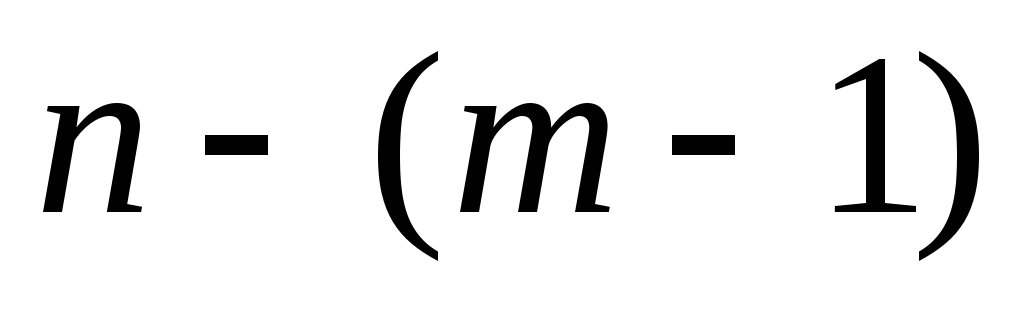 новых сглаженных уровней.
новых сглаженных уровней.
Первые и последние
![]() членов ряда с помощью данного алгоритма
сгладить нельзя, так как их значения
теряются.
членов ряда с помощью данного алгоритма
сгладить нельзя, так как их значения
теряются.
Метод простой скользящей средней вполне приемлем, если графическое изображение ряда динамики напоминает прямую линию. В этом случае не искажается динамика исследуемого явления. Однако когда тренд выравниваемого ряда имеет изгибы и к тому же желательно сохранить мелкие волны, использовать для сглаживания ряда метод простой скользящей средней нецелесообразно, так как простая скользящая средняя может привести к значительным искажениям исследуемого процесса. В таких случаях более надежным является использование взвешенной скользящей средней.
Метод взвешенной скользящей средней.
Взвешенная скользящая средняя
отличается от простой скользящей средней
тем, что уровни, входящие в интервал
усреднения, суммируются с различными
весами. Это связано с тем, что аппроксимация
сглаживаемого ряда динамики в пределах
интервала сглаживания осуществляется
с использованием уровней, рассчитанных
по полиному![]() (здесь
(здесь![]() - порядковый номер уровня в интервале
сглаживания). Полином 1-го порядка
- порядковый номер уровня в интервале
сглаживания). Полином 1-го порядка![]() есть уравнение прямой, следовательно,
метод простой скользящей средней
является частным случаем метода
взвешенной скользящей средней.,
Коэффициенты полиномов находятся по
способу наименьших квадратов (тема 9).
есть уравнение прямой, следовательно,
метод простой скользящей средней
является частным случаем метода
взвешенной скользящей средней.,
Коэффициенты полиномов находятся по
способу наименьших квадратов (тема 9).
На первом этапе сглаживания по методу взвешенной средней определяются интервал сглаживания и порядок аппроксимирующего полинома - параболы. Считается, что при использовании полиномов высоких степеней и при меньших размерах интервалов сглаживание ряда динамики будет более «гибким».
Центральная ордината параболы принимается
за сглаженное значение соответствующего
фактическим данным уровня. Поскольку
отсчет времени в пределах интервала
сглаживания производится от его середины,
т.е. (![]() )
)![]() ,
то сглаженное значение уровня равно
параметру
,
то сглаженное значение уровня равно
параметру![]() подобранной параболы и является
соответствующей скользящей средней.
Поэтому для сглаживания нет необходимости
прибегать к процедуре подбора системы
парабол, так как величину
подобранной параболы и является
соответствующей скользящей средней.
Поэтому для сглаживания нет необходимости
прибегать к процедуре подбора системы
парабол, так как величину![]() можно получить как взвешенную среднюю
из
можно получить как взвешенную среднюю
из![]() уровней.
уровней.
Пример.Если в интервал сглаживания входят пять последовательных уровней ряда со сдвигом во времени на один шаг, а выравнивание проводится по полиному 2-го порядка, то коэффициенты полинома находятся из условия
![]()
Учитывая, что для нечетных
![]() ,
приходим к системе:
,
приходим к системе:
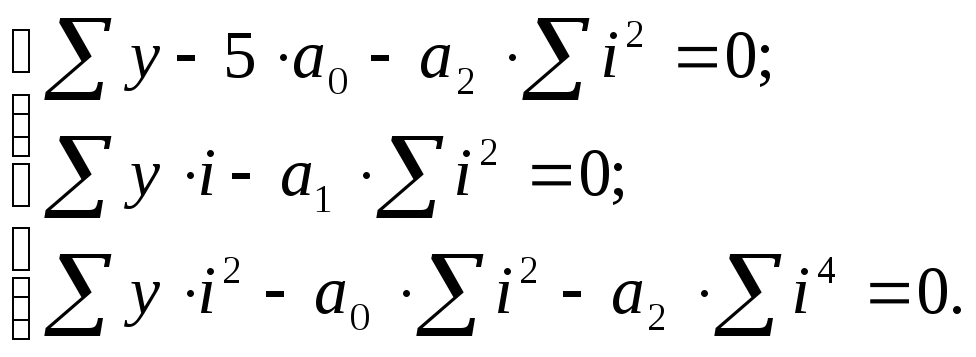
Для определения
![]() необходимо найти значения
необходимо найти значения![]() и
и![]()
Так как интервал сглаживания равен
![]() ,
то
,
то![]() и
и![]() .
.
Система нормальных уравнений для
определения
![]() и
и![]() в этом случае записывается так:
в этом случае записывается так:
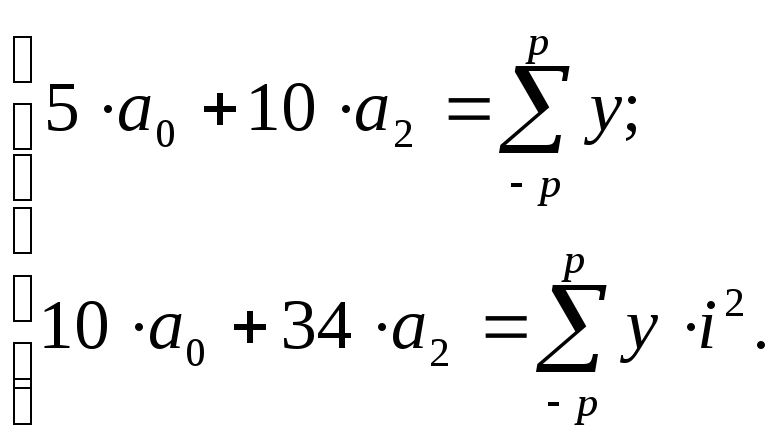
Решение этой системы относительно
![]() может быть представлено следующим
образом:
может быть представлено следующим
образом:
|
|
(10.23) |
Аналогичным путем получим выражения и для других интервалов сглаживания по параболе второго и третьего порядка. Так, например, для
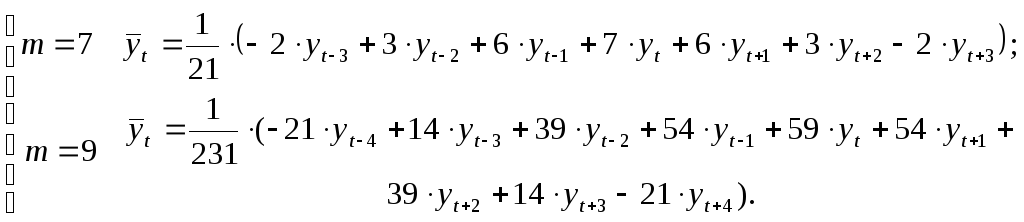
Согласно приведенным формулам веса
симметричны относительно центрального
уровня (![]() )
и их сумма с учетом общего множителя,
вынесенного за скобки, равна 1.
)
и их сумма с учетом общего множителя,
вынесенного за скобки, равна 1.
Выбор уравнения тренда, отображающего развитие социально-экономических явлений во времени. Для отображения основной тенденции развития явлений во времени применяются полиномы разной степени, экспоненты, логистические кривые и другие функции.
Полиномы имеют следующий вид:
1-й степени –
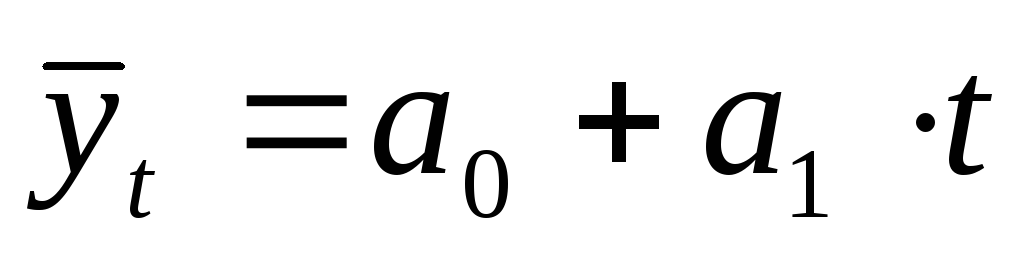 ;
;2-й степени –
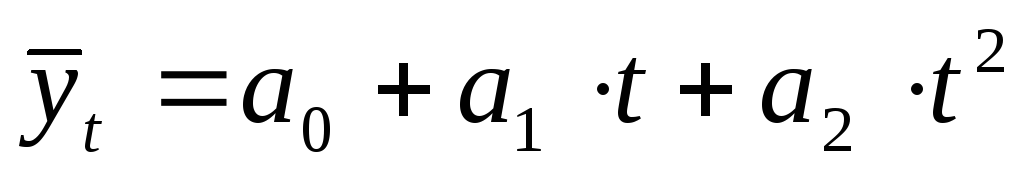 ;
;3-й степени –
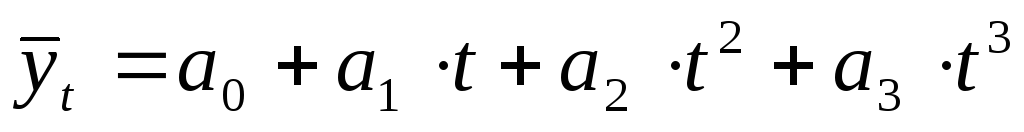 ;
;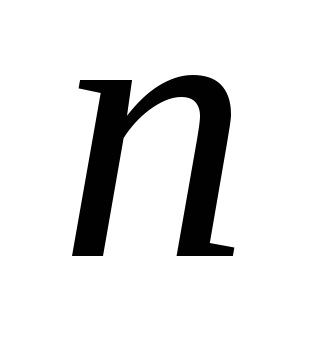 -й
степени –
-й
степени –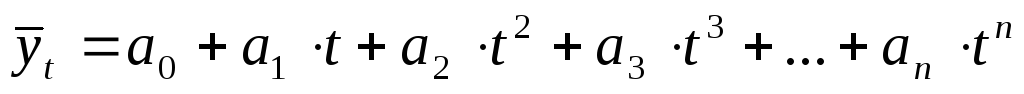 ,
,
|
где |
|
|
|
|
|
|
В статистической практике параметры
полиномов невысокой степени иногда
имеют конкретную интерпретацию
характеристик динамического ряда. Так,
параметр
![]() трактуется как характеристика средних
условий ряда динамики, параметры
трактуется как характеристика средних
условий ряда динамики, параметры![]() - изменение ускорения.
- изменение ускорения.
В статистике выработано правило выбора степени полинома модели развития, основанное на определении величин конечных разностей уровней динамических рядов. Согласно этому правилу полином 1-й степени (прямая) применяется как модель такого ряда динамики, у которого первые разности (абсолютные приросты) постоянны;полиномы 2-й степени - для отражения ряда динамики с постоянными вторыми разностями (ускорениями);полиномы 3-й степени - с постоянными третьими разностями и т.д.
Для полиноминальных моделей характерно отсутствие прямой связи между абсолютными приростами и приростами уровней рядов динамики.
Предполагаемой функцией, отражающей
процесс роста явления, может быть и
экспонента
![]() или
или![]() .
Экспоненты характеризуют прирост,
зависящий от величины основания функции.
.
Экспоненты характеризуют прирост,
зависящий от величины основания функции.
Отдельные уравнения выражают различные типы динамики.
Монотонное возрастание или убывание процесса характеризуют функции:
линейная;
параболическая;
степенная;
экспоненциальная простая (показательная) и производная от нее логарифмическая линейная;
сложная экспоненциальная и производная от нее логарифмическая парабола;
гиперболическая (главным образом убывающих процессов);
комбинация их видов.
Для моделирования динамических рядов, проявляющих быстрое развитие в начале ряда и затухающее его развитие к концу, т.е. тех, которые характеризуются стремлением к некоторой предельной величине, применяются логистические функции.
Логистическую функцию часто записывают в следующем виде:
![]() или
или![]()
|
где |
|
|
Логистическая кривая симметрична
относительно точки перегиба и при
![]() стремится к нулю, а при
стремится к нулю, а при![]() стремится к некоторой постоянной
величине, к которой кривая асимптотически
приближается. Если найти вторую
производную от
стремится к некоторой постоянной
величине, к которой кривая асимптотически
приближается. Если найти вторую
производную от![]() по
по![]() и приравнять ее к нулю, то для
логистической кривой, выражаемой через
местоположение точки перегиба кривой,
и приравнять ее к нулю, то для
логистической кривой, выражаемой через
местоположение точки перегиба кривой,![]() ;
;![]() .
.
Тип процессов, характеризующийся наличием экстремальных значений, описывается кривой Гомперца, имеющей следующее уравнение:
![]() .
.
Возможны четыре варианта этой кривой.
Для экономистов наибольшее значение
имеет кривая, у которой
![]() и
и![]() .
Развитие уровня такой кривой имеет
следующие этапы. Если коэффициент
.
Развитие уровня такой кривой имеет
следующие этапы. Если коэффициент![]() меньше 1 при отрицательном значении
меньше 1 при отрицательном значении![]() ,
то на первом этапе прирост кривой
незначителен. Он медленно увеличивается
по мере роста
,
то на первом этапе прирост кривой
незначителен. Он медленно увеличивается
по мере роста![]() ,
но на следующем этапе прирост
увеличивается быстрее, а затем, после
точки перегиба, начинает уменьшаться,
и на подходе к линии асимптоты прирост
кривой опять незначителен.
,
но на следующем этапе прирост
увеличивается быстрее, а затем, после
точки перегиба, начинает уменьшаться,
и на подходе к линии асимптоты прирост
кривой опять незначителен.
 или
или