ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 01.08.2024
Просмотров: 166
Скачиваний: 0
СОДЕРЖАНИЕ
Тема 10 статистическое изучение динамики социально-экономических явлений
Понятие и классификация рядов динамики
10.2 Сопоставимость уровней и смыкание рядов динамики
10.3 Аналитические показателиизменения уровней ряда динамики
10.5 Виды трендовой компоненты и проверка гипотезы о существовании тенденции
10.6 Методы анализа основной тенденции (тренда) в рядах динамики
10.7 Методы выявления периодической компоненты. Модели сезонных колебаний
10.8 Регрессионный анализ связных динамических рядов
Другой способ смыкания рядов динамики заключается в том, что уровни года, в котором произошли изменения, как до изменений, так и после изменения принимаются за 100%, а остальные пересчитываются в процентах по отношению к этим уровням соответственно. В результате получаем сомкнутый ряд динамики.
Приведение рядов динамики к одному основанию. Та же проблема приведения к сопоставимому виду возникает и при параллельном анализе развития во времени экономических показателей отдельных стран, административных и территориальных районов. Это, во-первых, вопрос о сопоставимости цен сравниваемых стран, во-вторых, о сопоставимости методики расчета сравниваемых показателей. В таких случаях ряды динамики приводятся кодному основанию, т.е. к одному и тому же периоду или моменту времени, уровень которого принимается за базу сравнения, а все остальные уровни выражаются в виде коэффициентов или в процентах по отношению к нему.
Коэффициент опережения (замедления).
Чтобы ответить на вопрос, во сколько
раз сравниваемый показатель одного
региона превышает аналогичный показатель
другого региона, необходимо сравнить
базисные коэффициенты роста за изучаемый
период, т.е. вычислитькоэффициент
опережения (замедления) -
![]() :
:
![]() ,
где (
,
где (![]() )
)
или
![]() ,
где (
,
где (![]() )
)
Эту формулу удобнее применять в том случае, когда ряд представляет постоянное повышение. Для рядов, где нет ярко выраженной тенденции к росту, удобнее за основание к приведению рядов брать средние показатели рядов динамики, в частности, средние темпы роста:
![]() ,
или
,
или![]()
10.3 Аналитические показателиизменения уровней ряда динамики
Анализ скорости и интенсивности развития явления во времени осуществляется с помощью аналитических показателей, которые получаются в результате сравнения уровней ряда динамики между собой. К таким показателям относятся: абсолютный прирост, темп роста и прироста, абсолютное значение 1% прироста. При этом принято сравниваемый уровень называть отчетным, а уровень, с которым производят сравнение, -базисным.
Аналитические показатели рада динамики.Абсолютный прирост (![]() )
характеризует размер увеличения (или
уменьшения) уровня ряда за определенный
промежуток времени. Он равен разности
двух сравниваемых уровней и выражает
абсолютную скорость роста:
)
характеризует размер увеличения (или
уменьшения) уровня ряда за определенный
промежуток времени. Он равен разности
двух сравниваемых уровней и выражает
абсолютную скорость роста:
|
|
(10.1) |
|
где |
|
|
Если
![]() ,
то уровень
,
то уровень![]() является предыдущим для данного ряда,
а абсолютные приросты изменения уровня
будут цепными. Если же
является предыдущим для данного ряда,
а абсолютные приросты изменения уровня
будут цепными. Если же![]() постоянно для данного ряда, то
абсолютные приросты будут базисными.
постоянно для данного ряда, то
абсолютные приросты будут базисными.
Интенсивность изменения уровня оценивается отношением отчетного уровня к базисному, которое всегда представляет собой положительное число.
Показатель интенсивности изменения уровня ряда в зависимости от того, выражается ли он в виде коэффициента или в процентах, принято называть коэффициентом роста илитемпом роста. Иными словами, коэффициент роста и темп роста представляют собой две формы выражения интенсивности изменения уровня. Однако необходимо отметить, что не нужно пользоваться одновременно двумя формами, которые по существу идентичны. Разница между ними заключается только в единице измерения.
Коэффициент роста показывает, во сколько раз данный уровень ряда больше базисного уровня (если этот коэффициент больше единицы) или какую часть базисного уровня составляет уровень текущего периода за некоторый промежуток времени (если он меньше единицы). В качестве базисного уровня в зависимости от цели исследования может приниматься какой-то постоянный для всех уровень (часто начальный уровень ряда) либо для каждого последующего предшествующий ему:
|
|
(10.2) |
В первом случае говорят о базисных темпах роста, во втором - о цепных темпах роста.
Наряду с темпом роста можно рассчитать показатель темпа прироста, характеризующий относительную скорость изменения уровня ряда в единицу времени. Темп прироста показывает, на какую долю (или процент) уровень данного периода или момента времени больше (или меньше) базисного уровня.
Темп прироста есть отношение абсолютного прироста к уровню ряда, принятого за базу:
|
|
(10.3) |
Если темп роста всегда положительное число, то темп прироста может быть положительным, отрицательным и равным нулю.
В статистической практике часто вместо расчета и анализа темпов роста и прироста рассматривают абсолютное значение одного процента прироста. Оно представляет собой одну сотую часть базисного уровня и в то же время - отношение абсолютного прироста к соответствующему темпу прироста:
|
|
(10.4) |
|
где |
|
|
Абсолютное значение 1% прироста служит косвенной мерой базисного уровня и вместе с темпом прироста позволяет рассчитать абсолютный прирост уровня за рассматриваемый период, т.е. он показывает, сколько абсолютных единиц приходится на 1% прироста (уменьшения).
Абсолютным ускорением в статистике
называется разность между последующим
и предыдущим абсолютными приростами
(![]() ).
Ускорение показывает, насколько данная
скорость больше (меньше) предыдущей.
).
Ускорение показывает, насколько данная
скорость больше (меньше) предыдущей.
Таким образом, абсолютное ускорение
есть скорость изменения скорости. Оно
может быть положительным и отрицательным
числом.. Относительным ускорением
называется отношение абсолютного
ускорения к абсолютному приросту,
принятому за базу (![]() ),
т.е. относительное ускорение есть темп
прироста абсолютного прироста. Оно
вычисляется лишь в том случае, если
абсолютный прирост, принятый за базу
сравнения, число положительное.
),
т.е. относительное ускорение есть темп
прироста абсолютного прироста. Оно
вычисляется лишь в том случае, если
абсолютный прирост, принятый за базу
сравнения, число положительное.
Средние обобщающие показатели ряда
динамики. Средний уровень ряда
динамики (![]() )
рассчитывается по средней хронологической.Средней хронологической называется
средняя, исчисленная из значений,
изменяющихся во времени. Такие средние
обобщают хронологическую вариацию. В
хронологической средней отражается
совокупность тех условий, в которых
развивалось изучаемое явление в данном
промежутке времени.
)
рассчитывается по средней хронологической.Средней хронологической называется
средняя, исчисленная из значений,
изменяющихся во времени. Такие средние
обобщают хронологическую вариацию. В
хронологической средней отражается
совокупность тех условий, в которых
развивалось изучаемое явление в данном
промежутке времени.
Методы расчета среднего уровня интервального и моментного рядов динамики различны. Для интервальных рядов с равноотстоящими уровнями средний уровень находится по формуле средней арифметической простой, а для неравноотстоящих уровней - по средней арифметической взвешенной:
|
|
(10.5) |
|
|
(10.6) |
|
где |
|
|
|
|
|
|
|
|
|
|
Средний уровень моментного ряда динамики так исчислять нельзя, так как отдельные уровни содержат элементы повторного счета. Средний уровень моментного равноотстоящего ряда динамики находится по формуле средней хронологической простой:
|
или
|
(10.7) |
Средний уровень моментных рядов динамики с неравноотстоящими уровнями определяется по формуле средней хронологической взвешенной:
|
|
(10.8) |
|
где |
|
|
|
|
|
|
Обобщающим показателем скорости
изменения явления во времени является
средний абсолютный прирост (![]() ).
).
Этот показатель дает возможность установить, насколько в среднем за единицу времени должен увеличиваться уровень ряда (в абсолютном выражении), чтобы, отправляясь от начального уровня за данное число периодов (например, лет), достигнуть конечного уровня. Определяющим свойством интересующего нас показателя среднего абсолютного прироста при такой постановке задачи является общий абсолютный прирост за весь период, ограничивающий ряд динамики. Для его определения воспользуемся формулой средней арифметической простой:
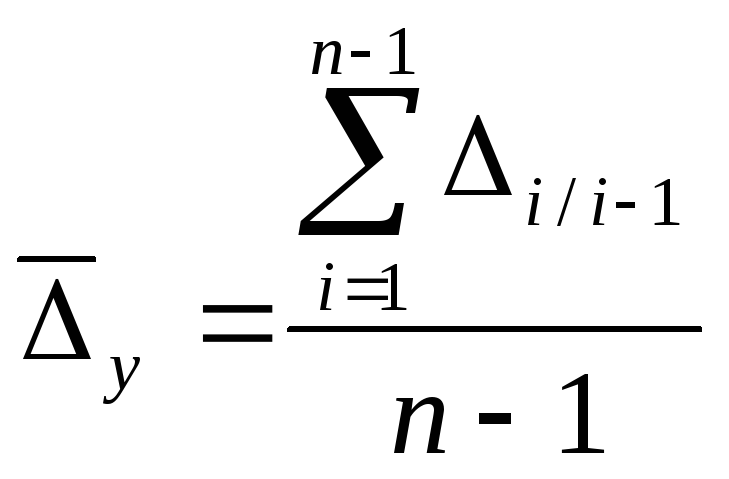
или
|
|
(10.9) |
Возможен и другой способ расчета среднего абсолютного прироста исходя из кумулятивных данных:
|
|
(10.10) |
Обе формулы применяются в зависимости от цели исследования.
Сводной обобщающей характеристикой интенсивности изменения уровней ряда динамики служит средний темп роста, показывающий, во сколько раз в среднем за единицу времени изменился уровень динамического ряда.
Необходимость исчисления среднего
темпа роста возникает вследствие того,
что темпы роста из года в год колеблются.
Кроме того, средний темп роста следует
определить в тех случаях, когда имеются
данные об уровне в начале какого-либо
периода и в конце его, а промежуточные
данные отсутствуют. Такого рода средний
темп роста можно исчислить, если положить
в основу расчетов рост не в арифметической
прогрессии, которая характеризуется
постоянной разностью, а геометрической
(![]() ),
характеризующейся постоянным
отношением, называемым знаменателем
прогрессии (
),
характеризующейся постоянным
отношением, называемым знаменателем
прогрессии (![]() ).
Следовательно, вопрос состоит в том,
чтобы найти этот знаменатель.Знаменатель
геометрической прогрессии (
).
Следовательно, вопрос состоит в том,
чтобы найти этот знаменатель.Знаменатель
геометрической прогрессии (![]() )
определяется делением последующего
уровня прогрессии на его предыдущий.
При делении
)
определяется делением последующего
уровня прогрессии на его предыдущий.
При делении![]() -го
уровня на первый получаем:
-го
уровня на первый получаем:
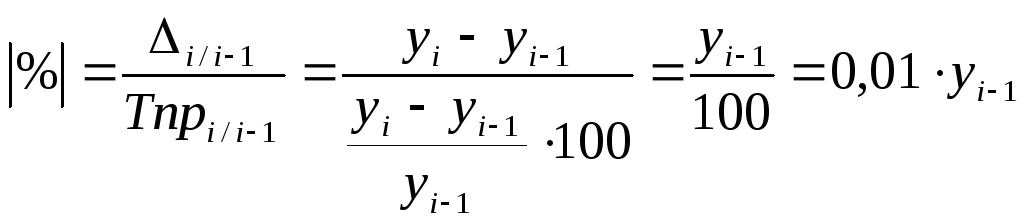 ,
,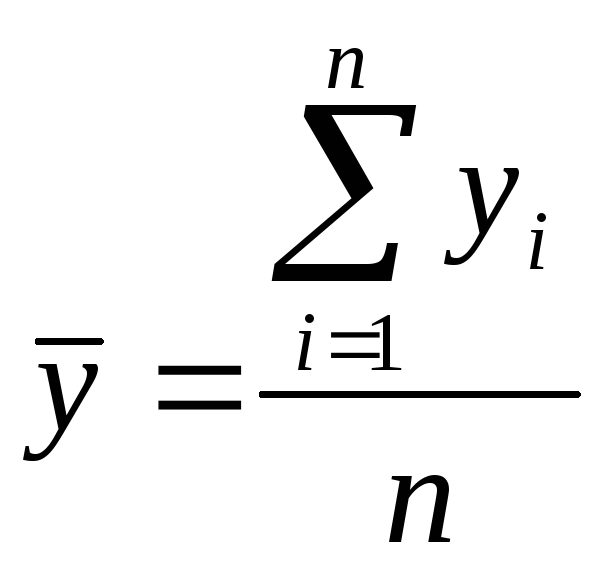 ;
;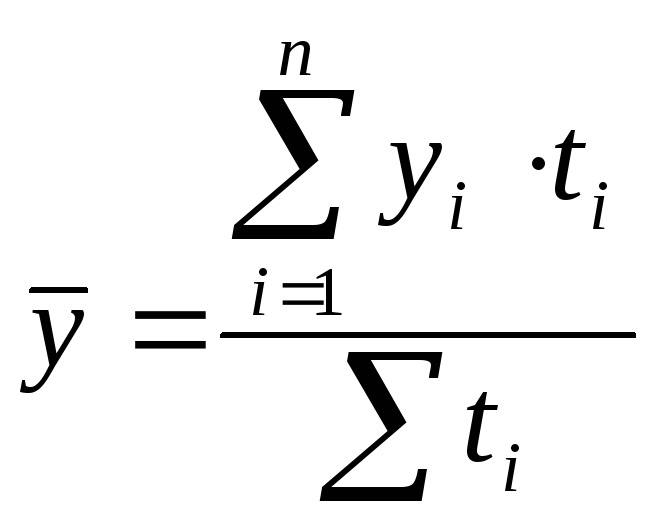 ,
,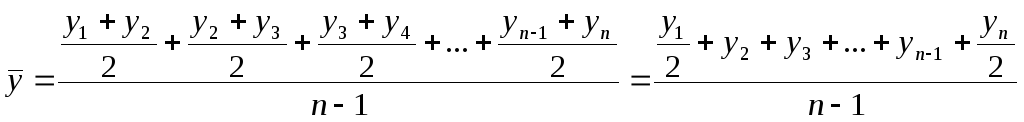
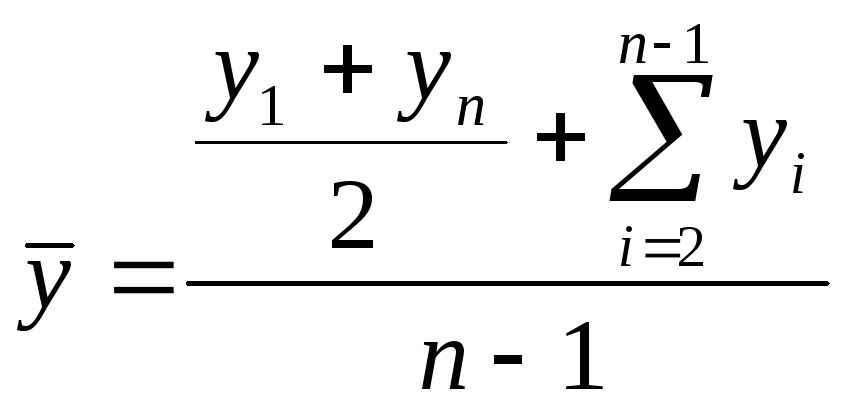 .
.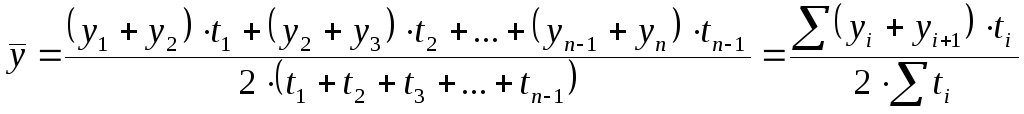 ,
,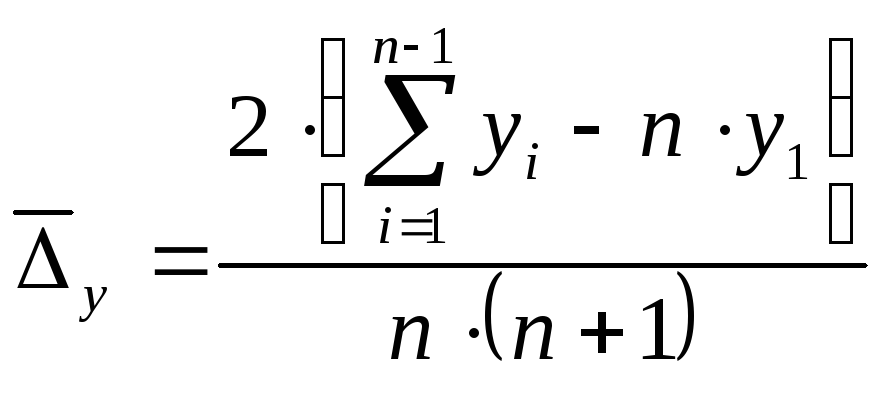 .
.