ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.08.2024
Просмотров: 91
Скачиваний: 0
СОДЕРЖАНИЕ
Многоэлектронные атомы. Заполнение электронных оболочек Конспект лекции (с демонстрациями)
Оценка энергии атомов в основном состоянии
Электронное строение атомов и их свойства
2. Атомный номер элемента. Изотопы
4. Волновые свойства электрона
5. Квантово-механическая модель атома
Не будем далее продолжать перечень элементов (подробно порядок заполнения электронных оболочек описан в приведенной ниже литературе и наглядно демонстрируется в простой модели). Рассмотренные примеры показывают, что квантовая механика на основе электронных структур атомов удовлетворительно описывает все основные закономерности периодической системы элементов Менделеева.
Подведем итоги:
основываясь на соотношении неопределенности, можно получить разумные оценки энергии основного состояния и размера многоэлектронных атомов;
состояние электрона в атоме задается значением четырех квантовых чисел: главного n, орбитального l, магнитного m и проекции спина ms;
два принципа: Паули и минимума энергии лежат в основе заполнения электронных состояний;
атомы действительно имеют те свойства, что следуют из предсказанных квантовой механикой электронных конфигураций.
Квантовые числа электрона
-
Квантовое число n – главное . Оно определяет энергию электрона в атоме водорода и одноэлектронных системах (He +, Li 2+ и т. д.). В этом случае энергия электрона
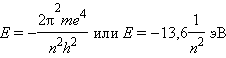
n принимает значения от 1 до ∞. Чем меньше n, тем больше энергия взаимодействия электрона с ядром. При n = 1 атом водорода находится в основном состоянии, при n > 1 – в возбужденном.
-
В многоэлектронных атомах электроны с одинаковыми значениямиn образуют слой или уровень, обозначаемый буквами K, L, M, N, O, P и Q. Буква K соответствует первому уровню, L – второму и т. д.
Модель 2.2. Атом водорода.
-
Орбитальное квантовое число l характеризует форму орбиталей и принимает значения от 0 до n – 1. Кроме числовых l имеет буквенные обозначения
l
=
0
1
2
3
4
…
l
=
s
p
d
f
g
…
Электроны с одинаковым значением l образуют подуровень.
Квантовое число l определяет квантование орбитального момента количества движения электрона
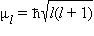 в
сферически симметричном кулоновском
поле ядра.
в
сферически симметричном кулоновском
поле ядра.-
Квантовое число m l называют магнитным . Оно определяет пространственное расположение атомной орбитали и принимает целые значения от –l до +l через нуль, то есть 2l + 1 значений. Расположение орбитали характеризуется значением проекции вектора орбитального момента количества движения M z на какую-либо ось координат (обычно ось z):
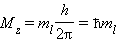
-
Все вышесказанное можно представить таблицей:
Орбитальное квантовое число
Магнитное квантовое число
Число орбиталей с данным значением l
l
m l
2l + 1
0 (s)
0
1
1 (p)
–1, 0, +1
3
2 (d)
–2, –1, 0, +1, +2
5
3 (f)
–3, –2, –1, 0, +1, +2, +3
7
Таблица 2.1.
Число орбиталей на энергетических подуровнях.
Орбитали одного подуровня (l = const) имеют одинаковую энергию. Такое состояние называют вырожденным по энергии. Так p-орбиталь – трехкратно, d – пятикратно, а f – семикратно вырождены.
-
Граничные поверхности s-, p-, d-, f- орбиталей показаны на рис. 2.1.
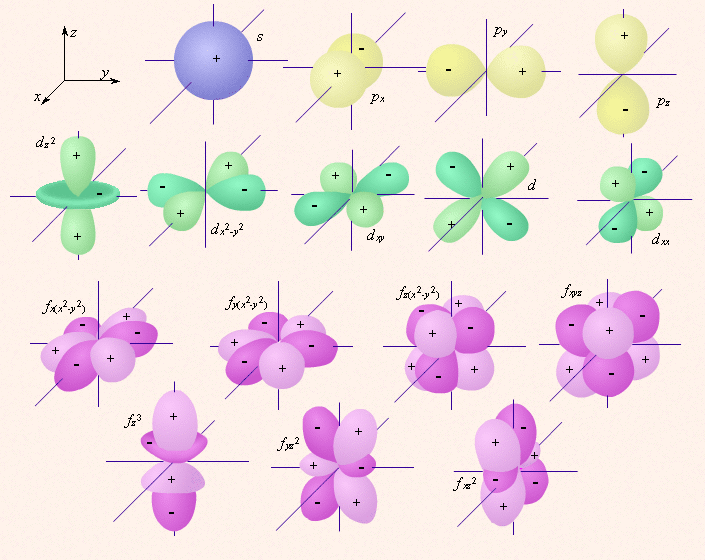
Рисунок 2.1.
Изображение с помощью граничных поверхностей s -, p -, d - и f -орбиталей.
s -Орбитали сферически симметричны для любого n и отличаются друг от друга только размером сферы. Их максимально симметричная форма обусловлена тем, что при l = 0 и μ l = 0.
p -Орбитали существуют при n ≥ 2 и l = 1, поэтому возможны три варианта ориентации в пространстве: m l = –1, 0, +1. Все p-орбитали обладают узловой плоскостью, делящей орбиталь на две области, поэтому граничные поверхности имеют форму гантелей, ориентированных в пространстве под углом 90° друг относительно друга. Осями симметрии для них являются координатные оси, которые обозначаются p x, p y, p z.
d -Орбитали определяются квантовым числом l = 2 (n ≥ 3), при котором m l = –2, –1, 0, +1, +2, то есть характеризуются пятью вариантами ориентации в пространстве. d-Орбитали, ориентированные лопастями по осям координат, обозначаются d z ² и d x ²–y², а ориентированные лопастями по биссектрисам координатных углов – d xy, d yz, d xz.
Семь f-орбиталей, соответствующих l = 3 (n ≥ 4), изображаются в виде граничных поверхностей, приведенных на рис. 2.1.
Квантовые числа n, l и m l не полностью характеризуют состояние электрона в атоме. Экспериментально установленно, что электрон имеет еще одно свойство – спин. Упрощенно спин можно представить как вращение электрона вокруг собственной оси.Спиновое квантовое число m s имеет только два значения m s = ±1/2, представляющие собой две проекции углового момента электрона на выделенную ось. Электроны с разными m sобозначаются стрелками, направленными вверх
 и
вниз
и
вниз  .
.-
В многоэлектронных атомах, как и в атоме водорода, состояние электрона определяется значениями тех же четырех квантовых чисел, однако в этом случае электрон находится не только в поле ядра, но и в поле других электронов. Поэтому энергия в многоэлектронных атомах определяется не только главным, но и орбитальным квантовым числом, а вернее их суммой: энергия атомных орбиталей возрастает по мере увеличения суммы n + l; при одинаковой сумме сначала заполняется уровень с меньшим n и большим l. Энергия атомных орбиталей возрастает согласно ряду
1s < 2s < 2p < 3s < 3p < 4s ≈ 3d < 4p < 5s ≈ 4d < 5p < 6s ≈ 4f ≈ 5d < 6p < 7s ≈ 5f ≈ 6d < 7p.
Итак, четыре квантовых числа описывают состояние электрона в атоме и характеризуют энергию электрона, его спин, форму электронного облака и его ориентацию в пространстве. При переходе атома из одного состояния в другое происходит перестройка электронного облака, то есть изменяются значения квантовых чисел, что сопровождается поглощением или испусканием атомом квантов энергии.
Главное квантовое число n в значительной степени определяет значение энергии электрона в атоме и размеры электронного облака. Оно принимает положительные целочисленные значения от 1 до бесконечности. С ростом n возрастают размеры электронного облака и энергия электронов. Вспомните, в теории Бора энергия электрона пропорциональна
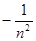 !
!Кроме цифрового обозначения n используется и буквенная индексация:
n = 1, 2, 3, 4 …
K, L, M, N …
Совокупность электронов, характеризующихся одним и тем же значением главного квантового числа, называют электронным слоем (школьное название – электронный уровень). Соответственно говорят о первом или K-слое, втором или L-слое, третьем или M-слое и т.д.
Второе квантовое число (ℓ), называемое орбитальным (побочным, в иностранной литературе – азимутальным) квантовым числом, характеризует энергию электрона внутри слоя (уровня) и определяет форму электронного облака. Оно принимает положительные целочисленные значения, начиная с нуля, но имеет ограничение: при данном значении главного квантового числа n величина ℓ не может превысить значение (n–1). На практике побочное квантовое число чаще обозначается буквами:
ℓ = 0, 1, 2, 3, 4,…, n–1
s, p, d, f, g,…
Совокупность электронов c одним и тем же значением побочного квантового числа называют электронной оболочкой (подуровнем). Соответственно говорят об s-, p-, d-, f- и т. д. оболочках.
Третье квантовое число (mℓ), называемое магнитным, определяет ориентацию орбитали в пространстве. Орбиталь же образуется совокупностью электронов с одним и тем же значением магнитного квантового числа, её традиционно обозначают клеточкой ٱ (квантовая ячейка). При данном значении ℓ, магнитное квантовое число принимает значения:
1, 2, 3, 4, …, ℓ
mℓ = 0
–1, –2, –3, –4, …, –ℓ
Общее число значений составляет (2ℓ+1).
Названные три квантовых числа непосредственно вытекают из решения уравнения Шредингера в трёхмерном мире. У электрона есть и четвертая квантовая характеристика – спиновое квантовое число ms, отражающее четвёртую координату нашего мира – время. Спиновое квантовое число принимает (в единицах атомного мира) лишь два значения: +½ и –½. Договоримся считать значение +½ больше значения –½ и будем обозначать электроны со спином +½ стрелочкой , а электроны со спином –½ – стрелочкой ¯.
Четыре квантовых числа есть полная и однозначная характеристика состояния электрона в атоме. Более того, в атоме не может быть двух электронов с одинаковым набором четырёх квантовых чисел (принцип Паули). Это – основной закон мира электронов. Принцип Паули позволяет рассчитать максимальное число электронов в слое, оболочке и на орбитали.



 Орбиталь
характеризуется постоянным значением
mℓ.
Это возможно лишь при известном значении
ℓ, что в свою очередь требует постоянства
значения n. Таким образом, для орбитали
изменяется только спиновое квантовое
число, отсюда следует, что на орбитали
может быть максимально два электрона
и они в соответствии с принципом Паули
обязательно должны иметь противоположные
спины: ¯ .
Орбиталь
характеризуется постоянным значением
mℓ.
Это возможно лишь при известном значении
ℓ, что в свою очередь требует постоянства
значения n. Таким образом, для орбитали
изменяется только спиновое квантовое
число, отсюда следует, что на орбитали
может быть максимально два электрона
и они в соответствии с принципом Паули
обязательно должны иметь противоположные
спины: ¯ .






 Возникает
вопрос, а если на орбитали находится
один электрон, то каково его состояние:
или ¯ ? Эта проблема регулируется правилом
Хунда: суммарный
спин электронов оболочки должен быть
максимальным.
Таким образом, в рамках принятых
договорённостей единственный электрон
на орбитали имеет спиновое квантовое
число +½.
Возникает
вопрос, а если на орбитали находится
один электрон, то каково его состояние:
или ¯ ? Эта проблема регулируется правилом
Хунда: суммарный
спин электронов оболочки должен быть
максимальным.
Таким образом, в рамках принятых
договорённостей единственный электрон
на орбитали имеет спиновое квантовое
число +½.Оболочка характеризуется постоянным значением орбитального квантового числа, что возможно при известном значении главного квантового числа. Следовательно, для оболочки происходит изменение магнитного и спинового квантового чисел. При значении орбитального квантового числа равном ℓ число разрешённых значений магнитного квантового числа, а значит и число орбиталей в этой оболочке составляет (2ℓ+1) штук (ℓ положительных, ℓ отрицательных и ноль). Отсюда получаем, что максимальное число электронов в оболочке составит 2(2ℓ+1) или конкретно: для s-оболочки 2; для p-оболочки 6; для d-оболочки 10; для f-оболочки 14 и т.д.
Наконец, для нахождения максимального числа электронов, могущих быть в данном слое, необходимо суммировать электроны всех оболочек этого слоя. Для слоя с главным квантовым числом n это будут оболочки с ℓ =0, 1, 2, 3, …, n –1. Следовательно, ёмкость слоя составит:
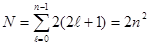
Методом математической индукции легко показать, что эта сумма равна 2n2. Отсюда максимальное число электронов составит: в первом слое (К-слое) 2; во втором слое (L-слое) 8; в третьем слое (М-слое) 18 и т.д.
Энергия электрона в атоме водорода (теория Бора) определяется единственным (главным) квантовым числом, а в многоэлектронном атоме – главным и орбитальным квантовыми числами. В целом энергия электрона возрастает по мере роста суммы названных квантовых чисел при доминирующем значении главного квантового числа. При одинаковой сумме энергия состояния с меньшим значением главного квантового числа ниже. В соответствии с этими правилами энергетический ряд атомных орбиталей выглядит следующим образом:
1s < 2s < 2p < 3s< 3p < 4s < 3d < 4p < 5s < 4d < 5p < 6s <
< 4f < 5d < 6p < 7s < 5f < 6d < 7p …
Для изображения атомных орбиталей используют значения волновой функции или её квадрата (точнее угловой части этой функции). Поскольку электронная орбиталь в принципе распространяется до бесконечности, то изображают её часть (например, 80 или 90%). На рис. 1.5 представлены формы 1s-, 2p- и 3d-орбиталей.
1s-орбиталь сферически симметрична, знак соответствующей функции одинаков в разных частях системы координат. Три 2p-орбитали представляют собой объёмные гантелеобразные фигуры, прошитые соответствующими осями координат. Четыре из пяти 3d-орбиталей представляют собой двугантельные образования, различно ориентированные в пространстве. Знаки соответствующих функций для гантелей различны. Пятая 3d-орбиталь представляет собой массивную гантель, насаженную на ось z, и тороидальную катушку в плоскости xy.
Узловой поверхностью орбитали называют геометрическое место точек, где Ψ=0 (Ψ2=0). Узловые поверхности могут быть сферическими, плоскими и коническими. По определению каждая орбиталь имеет сферическую узловую поверхность с бесконечным радиусом.
Главное квантовое число равно общему числу узловых поверхностей данной орбитали. Например, любая из 3d-орбиталей имеет одну сферическую узловую поверхность и две плоские (две конические – для
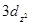 ).
).Побочное квантовое число равно числу узловых поверхностей орбитали, проходящих через начало координат. Например, любая из пяти
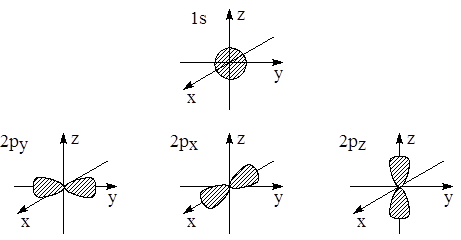
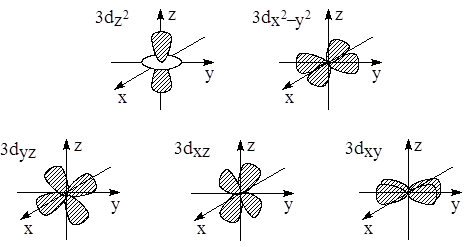
Рис. 1.5. Формы 1s, 2p и 3d-орбиталей
3d-орбиталей (ℓ=2) имеет по две узловые поверхности, проходящие через начало координат.
Отметим, что формы ns-орбиталей отличаются от формы 1s-орбитали, аналогично np-орбитали отличны от 2р-орбиталей. Однако при качественном рассмотрении вопросов химической связи, связанных с перекрыванием орбиталей, в определённом приближении можно считать любую s-орбиталь сферически симметричной, а любую р-орбиталь – гантелеподобной.
Строение атома
1. Ядро и электроны
Развитие естествознания на границе XIX-XX веков показало, что помимо химических превращений существует целый ряд процессов, в которых атомы выступают как сложные объекты, состоящие из положительно заряженной части - ядра и отрицательно заряженных электронов, суммарный заряд которых в точности компенсирует заряд ядра. В результате работ английского физика Дж. Дж. Томсона и американского физика Р.С. Малликена было установлено, что электрон имеет массу 9,1*1031 кг, или 1/1837 массы атома водорода, и заряд 1,6*10 19 Кл. Основная масса атома сосредоточена в ядре, которое занимает очень малую часть его объема: диаметр ядра порядка 1СГ14 м, он составляет лишь около 10 4 диаметра атома. Наглядно это соотношение размеров можно представить себе, если увеличить атом в 1011 раз: тогда ядро диаметром 1 мм разместится внутри атома диаметром 10 метров!
Позднее было показано, что атомные ядра состоят из положительно заряженных частиц - протонов и незаряженных частиц - нейтронов. Протон имеет заряд, равный заряду электрона, но со знаком плюс, его масса практически равна массе нейтрона. Отметим, что в химии принято выражать заряды ионов в единицах заряда электрона с соответствующим знаком, например Н+, Mg2+, СГ.
Таким образом, число протонов в ядре определяет его заряд и порядковый номер, а сумма чисел протонов и нейтронов - округленную общую массу ядра в атомных единицах, или массовое число атома. Очевидно, что в электронейтральном атоме число протонов в атомном ядре равно числу электронов в электронной оболочке атома.
2. Атомный номер элемента. Изотопы
Порядковый номер элемента принято называть его атомным номером и обозначать буквой Z. Атомный номер лежит в основе систематизации химических элементов и определяет их положение в периодической системе.
При определенном атомном номере, т.е. при определенном числе протонов, в ядре могут находиться разные числа нейтронов, поэтому могут существовать отличающиеся по массе разновидности атомов одного и того же элемента - изотопы.
Например, природный водород представляет собой смесь изотопов с массовыми числами 1 и 2, а.
Клетка периодической таблицы
В ядре атома урана 92 протона, а в его электронной оболочке - 92 электрона
В периодической таблице, элементы расположены в порядке увеличения заряда ядра, а в отдельных клеточках таблицы принято приводить средневзвешенные атомные массы, поэтому они часто сильно отличаются от целочисленных.
Рис. 2.3, а. Масс-спектрометр.
Газ вводится в вакуумированный прибор через трубку (i) и подвергается ионизации потоком электронов из электронной пушки (2). Заряженные пластины (3) и (4) разгоняют поток полученных положительных ионов, который проходит че-рез щель в пластине (4) и попадает в поле магнита (5), отклоняющее отдельные ионы в соответствии с отношением заряд: масса. За второй щелью (в) расположен детектор (7), который регистрирует число частиц, прошедших через щель. Меняя напряженность магнитного поля, можно последовательно регистрировать относительное количество ионов с различной массой, получая масс-спектр.
В масс-спектрометре молекулы газа превращаются в ионы. Показана часть масс-спектра, соответствующая нонам ТЮ+ и ТЮ2. Отдельные полосы отвечают пяти изотопам титана с массой 46, 47, 48, 49, 50 значений масс атомов и разделение изотопов стало возможным в результате создания масс-спектрометрии - метода, основанного на воздействии магнитного поля на направленные пучки заряженных частиц.
3. Ядерная модель атома
Первая модель атома была предложена в начале XX века Э. Резерфордом, новозеландцем, работавшем в Англии. Она предполагала, что электроны движутся с большой скоростью по круговым орбитам вокруг ядра, подобно планетам по отношению к Солнцу. По представлениям классической электромагнитной теории в таком атоме электрон должен приближаться по спирали к ядру, непрерывно излучая энергию. Через короткое время электрон неизбежно должен упасть на ядро. Это очевидное несоответствие фактам было не единственным недостатком модели Резерфорда: плавное изменение энергии электронов в атоме не согласовывалось с появившимися наблюдениями над спектрами атомов. Одним из достижений второй половины XIX века была разработка атомного спектрального анализа - точного и чувствительного метода, сыгравшего важнейшую роль в открытии новых элементов и послужившего экспериментальной основой изучения строения атомов. Метод основан на испускании света свободными атомами, получающимися при сильном нагреваний вещества; при этом атомы переходят из основного состояния с минимальной энергией в возбужденные состояния с более высокими энергиями.
Возвращаясь в основное состояние, атомы излучают свет. Оказалось, что атомные спектры излучения состоят из отдельных линий, отвечающих только определенным длинам волн.
Чтобы объяснить линейчатый характер атомных спектров и устойчивость атомов, знаменитый датский физик Нильс Бор предложил два постулата, выходящие за рамки классической физики:
Из бесконечного числа орбит, возможных с точки зрения классической механики, допустимы лишь определенные орбиты, по которым электрон движется не излучая.
Частота поглощаемого или испускаемого атомом излучения при переходе из одного разрешенного состояния в другое определяется разностью энергий этих состояний.
При этом Бор опирался на идею Макса Планка о квантовании энергии. Планк установил, что, хотя свет, испускаемый раскаленным телом, кажется сплошным, световая энергия поглощается или излучается отдельными порциями - квантами Е = hv, пропорциональными частоте светового электромагнитного колебания. Коэффициент пропорциональности h = 6,6252 * 10 34 Дж * с был назван постоянной Планка. Таким образом в науку было введено понятие кванта света, или некоторого светового пакета - фотона, отражающее не только волновую, но и корпускулярную природу света.
Модель Бора позволила рассчитать точные значения энергии атома водорода и любых одноэлектронных ионов, но оказалась непригодной для объяснения наблюдаемых энергетических характеристик атомов с двумя и более электронами; главный же ее недостаток заключался в том, что она не давала логического обоснования природы квантования и устойчивости не меняющихся во времени состояний атома. Однако, несмотря на эти недостатки, сами идеи Бора о квантовании и стационарных состояниях легли в основу современного описания строения атома с позиций квантовой механики.