ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 20.08.2024
Просмотров: 250
Скачиваний: 0
СОДЕРЖАНИЕ
4, 4, 2, 1, 4, 5 ,4, 3, 6, 5, 4, 4, 1, 2, 5, 4, 7, 3, 4, 2, 3, 1, 3, 2, 1, 2, 6.
Обобщающие статистические показатели
Статистическое изучение динамики
Статистическое изучение взаимосвязи социально-экономических явлений
Исходные данные для выполнения задания 15
Исходные данные для выполнения задания 21
Значения вероятностей, вычисленных для различных t (от 1 до 3)
Приложение 3 Величины коэффициента Стьюдента для различных значений доверительной вероятности
Приложение 4 Критические значения t-критерия Стьюдента для оценки значимости коэффициента корреляции
Среднее квадратическое отклонение заработной платы рабочих составит:
Сила влияния группировочного признака на вариацию анализируемого показателя определяется с помощью эмпирического коэффициента детерминации:
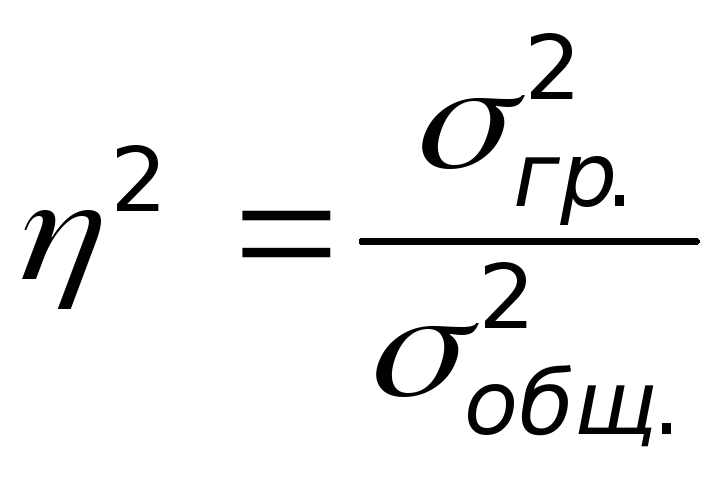
Теснота связи между группировочным и результативным показателями определяется с помощью эмпирического коэффициента корреляции:
=
Вывод…..……………………………………………………………..…………….
…………………………………………………………………………………………….……………………………………………………………………………………………….………………………………………………………………………………………………….
Задание 38. По двум фермам предприятия имеются следующие данные о молочной продуктивности коров и вариации их удоев:
|
Показатель |
Ферма № 1 |
Ферма № 2 |
|
Число коров, гол. |
200 |
400 |
|
Средний удой, ц |
40 |
30 |
|
Остаточная дисперсия |
4,00 |
2,25 |
Определите общую дисперсию и коэффициент вариации удоев по предприятию в целом. Сформулируйте выводы.
Решение. Определим средний уровень молочной продуктивности коров по предприятию в целом по формуле …
Для расчётов воспользуемся данными таблицы 26.
Таблица 26 – Исходные …
|
Средний удой, ц
|
Число коров, гол.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ИТОГО |
|
|
|
|
|
|
Рассчитывается общая дисперсия по правилу сложения дисперсий:
Групповая дисперсия рассчитывается по формуле:
Средняя из остаточных дисперсий определяется по формуле:
Среднее квадратическое отклонение:
Коэффициент вариации:
Вывод…..……………………………………………………………..…………….
…………………………………………………………………………………………….……………………………………………………………………………………………….………………………………………………………………………………………………….
Выборочное наблюдение
Задание 39. На заводе было взято 100 электроламп для проверки средней продолжительности горения. По ним выборочно определён ряд показателей. Так, средняя продолжительность горения составила 1500 ч, среднее квадратическое отклонение – 70 ч. Определите, в каких пределах заключена средняя продолжительность горения электроламп в генеральной совокупности с вероятностью 0,997.
Решение. Определяется, в каких пределах заключена средняя продолжительность горения электроламп в генеральной совокупности.
Д
ано:
?
Вывод…..……………………………………………………………..…………….
…………………………………………………………………………………………….……………………………………………………………………………………………….………………………………………………………………………………………………….
Задание 40. В сельскохозяйственной организации методом случайной бесповторной выборки было отобрано 100 овец для проверки среднего настрига шерсти. Получены следующие данные: средний настриг шерсти с одной овцы составил 3,36 кг, среднее квадратическое отклонение – 0,55 кг. Определите с вероятностью 0,997, в каких пределах заключён средний настриг шерсти с овцы во всей генеральной совокупности.
Решение. Определим, в каких пределах заключен средний настриг шерсти с одной овцы в сельскохозяйственной организации во всей генеральной совокупности.
Вывод…..……………………………………………………………..…………….
…………………………………………………………………………………………….……………………………………………………………………………………………….………………………………………………………………………………………………….
Д
ано:
?
Задание 41. В цеху изготовлена партия шестерён количеством 500 штук. Для определения веса шестерни было взято 45 штук. Их средний вес составил 620 г, а дисперсия – 10 г. С вероятностью 0,954 необходимо определить, какой был бы средний вес шестерни в генеральной совокупности при сплошном наблюдении.
Р
ешение.
Определяется, какой был бы средний вес
шестерни в генеральной совокупности
при сплошном наблюдении.
Дано:
?
Вывод…..……………………………………………………………..…………….
…………………………………………………………………………………………….……………………………………………………………………………………………….………………………………………………………………………………………………….
Задание 42. Механическим бесповторным отбором взято 256 голов из 500 голов родившихся поросят для определения их живой массы при рождении. Получены следующие характеристики: в среднем масса одного поросёнка при рождении составляет 891 г, среднее квадратическое отклонение в выборочной совокупности равно 82 г. Определите в каких пределах заключается средний вес поросёнка в генеральной совокупности с вероятностью 0,997.
Р
ешение.
Определим, в
каких пределах заключается средний вес
поросёнка в генеральной совокупности.
Дано:
?
Вывод…..……………………………………………………………..…………….
…………………………………………………………………………………………….……………………………………………………………………………………………….………………………………………………………………………………………………….
Задание 43. Случайной бесповторной выборкой 400 деталей установлено, что среди отобранных деталей 2 % бракованных. С вероятностью 0,954 найдите долю брака для всей совокупности, состоящей из 4000 деталей.
Решение. Определяется доля брака для всей совокупности.
Дано:
