ВУЗ: Московский технический университет связи и информатики
Категория: Учебное пособие
Дисциплина: Программирование
Добавлен: 23.10.2018
Просмотров: 6222
Скачиваний: 74
СОДЕРЖАНИЕ
Раздел 1. Основы работы с математическим пакетом Matlab
Тема 1.1. Элементы рабочей среды Matlab
1.1.1.Элементы рабочей среды Matlab и простейшие вычисления
1.1.2. Основные объекты системы Matlab
1.1.3. Лабораторная работа по теме «Элементы рабочей среды Matlab и простейшие вычисления»
1.2.2. Построение графиков и визуализация вычислений в системе MatLab
1.2.3. Лабораторная работа по теме
«Векторы, матрицы и построение графиков
1.2.4. Контрольные вопросы по теме
Тема 1.3. Средства Matlab для создания и описания m-файлов
Пример 1.3.5-1. Даны n чисел . Требуется вычислить их сумму: где
1.3.6. Лабораторная работа по теме
«Средства алгоритмизации и программирования
1.3.7. Контрольные вопросы по теме
Раздел 2. Технология решения вычислительных задач средствами MatLab
Тема 2.1. Решение нелинейных уравнений
2.1.2. Лабораторная работа по теме
«Технология решения нелинейных уравнений средствами пакета MatLab»
1. Вопросы, подлежащие изучению
2.1.3. Контрольные вопросы по теме
Тема 2.2. Технология аппроксимации интерполяции функций в среде пакета MatLab
Рис. 2.2.1-5. Вычисление функции в точке х=0.58
Рис. 2.2.2-7. Графики интерполирующих функций
Тема 2.4. Технология решения обыкновенных дифференциальных уравнений
Рис. 2.4.1-2. Решение ОДУ методом Рунге-Кутты четвертого порядка
1. Вопросы, подлежащие изучению
Тема 2.5. Технология решения задач одномерной оптимизации
2.5.2. Лабораторная работа по теме
«Технология решения задач одномерной оптимизации»
1. Вопросы, подлежащие изучению
3. Варианты индивидуальных заданий
2.5.3. Контрольные вопросы по теме
Тема 2.6. Технология решения задач многомерной оптимизации
Тема
1.2. Векторы, матрицы и
построение
графиков в системе Matlab
1.2.1. Вектора и матрицы
1.2.2. Построение графиков и визуализация вычислений в системе MatLab
1.2.3. Лабораторная работа по теме
1.2.4. Контрольные вопросы по теме
1.2.1. Векторы и матрицы
Matlab
построена как система, ориентированная
на работу с матрицами, то есть все
численные вычисления производятся в
матричной форме. Даже обычные числа и
переменные в Matlab
рассматриваются как матрицы размера 1
x 1. К
особенностям работы с массивами в Matlab
относится то, что одномерный массив
может быть вектором-строкой
или вектором-столбцом
(рис.
1.2.1-1).
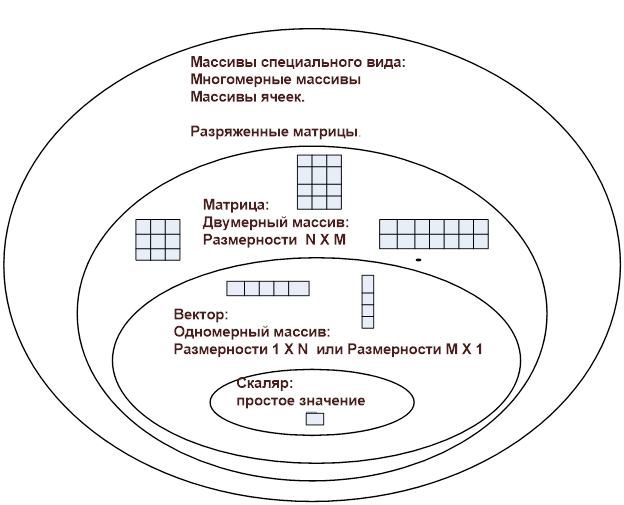
Рис.
1.2.1-1. Представление данных в Matlab:
переменные,
вектора (одномерные
массивы) и матрицы (двумерные массивы)
Для определения вектора используется операция квадратные скобки (операция объединения), а элементы вектора (рис. 1.2.1-2) отделяются друг от друга:
-
точкой с запятой, если нужно получить вектор-столбец;
-
пробелом или запятой, если нужно разместить элементы в векторе-строке.
|
|
Рис. 1.2.1-2. Создание вектора-строки a=[ ] и вектора-столбца b=[ ]
Для определения длины вектора используется функция length(а), где а – имя вектора, а для операции транспонирования используется символ апостроф (') (рис. 1.2.1-3).
|
|
Рис. 1.2.1-3. Определение длины вектора и его транспонирование
В следующем примере (рис. 1.2.1-4) при описании вектора х символ двоеточие, поставленный между двумя числами, указывает, что его элементы последовательно принимают значения, начиная от первого числа (0) до последнего числа (5) с шагом 1 (по молчанию шаг равен 1). При описании вектора y использован шаг 0.1, и выведены значения элементов вектора.
|
|
Рис. 1.2.1-4. Способы описания векторов с постоянным шагом
Для описания матрицы необходимо ввести ее имя и знак присваивания, а затем в квадратных скобках значения ее элементов. При этом значения элементов строк вводятся через пробел, а строки матрицы разделяет символ точка с запятой (;) (рис. 1.2.1-5):
А=[v1;v2;v3], где v1, v2, v3 - векторы одинаковой размерности.
|
|
Рис. 1.2.1-5. Создание матрицы A(3,4) и доступ к ее элементам
Следует помнить, что нумерация элементов матрицы (в строках и столбцах) начинается с 1.
Matlab обладает большим набором встроенных функций для обработки векторных данных. Полный список имеющихся функций выводится в командное окно при помощи команды help datafun. Некоторые из них приведены в таблице 1.2.1-1.
Таблица 1.2.1-1
|
Функции операции над векторами |
|
|
prod(V) |
Произведение элементов вектора |
|
sum(V) |
Сумма элементов вектора |
|
min(V) |
Минимальный элемент вектора |
|
max(V) |
Максимальный элемент вектора |
|
mean(V) |
Среднее значение элементов вектора |
|
sort(V) |
Сортировка элементов вектора по возрастанию (-sort(V) – по убыванию) |
|
Функции определения матриц и операций над ними |
|
|
det(A) |
Вычисляет определитель квадратной матрицы |
|
rand ([n,m]) |
Возвращает матрицу, элементы которой распределены по равномерному закону |
|
randn ([n,m]) |
Возвращает матрицу, элементы которой распределены по нормальному закону |
|
size(A) |
Определяет число строк и столбцов матрицы А, результат – вектор [n;m] |
|
sum(A [,k]) |
Формирует вектор-строку (k – есть) или вектор-столбец (k- нет), каждый элемент которого – сумма элементов строки или столбца |
|
min(А) |
Формирует вектор-столбец из минимальных элементов строк |
|
max(А) |
Формирует вектор-столбец из максимальных элементов строк |
|
sort(A) |
Упорядочивает элементы столбцов по возрастанию |
|
norm(A [,p]) |
Возвращает норму матрицы (по умолчанию вычисляется вторая норма) |
|
inv(A) |
Возвращает матрицу, обратную А |
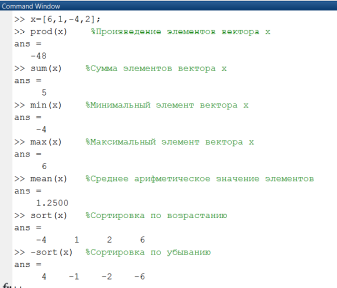
Примеры использования некоторых функций над векторами приведены на рис. 1.2.1-6.
|
|
Рис. 1.2.1-6. Примеры функции над векторами
|
|
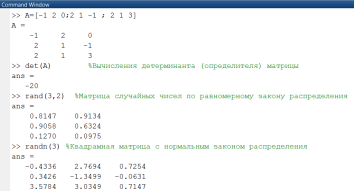
Рис. 1.2.1-7. Примеры определения матриц
На рис. 1.2.1-7 приведены примеры вычисления определителя квадратной матрицы и заполнения матриц случайными числами, сгенерированных по равномерному и нормальному законам.
В следующем примере (рис. 1.2.1-8) показано использование функции Matlab sum().
|
|
Рис. 1.2.1-8. Варианты использования функции Matlab sum()
Пример, приведенный на рис. 1.2.1-9, демонстрирует функции, определяющие минимальные и максимальные значения матриц.
|
|
Рис. 1.2.1-9. Определение минимальных и максимальных значений
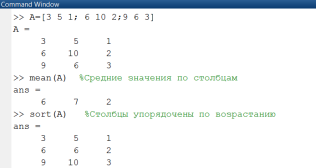
В примере, приведенном на рис. 1.2.1-10, показаны функции, позволяющие определять средние значения элементов в столбцах (или в строках) и проводить упорядочение (сортировку) элементов в строках (или столбцах).
|
|
Рис. 1.2.1-10. Определение средних значений и упорядочение элементов
Известно, что если детерминант матрицы отличен от нуля, то это невырожденная матрица. Для такой матрицы может быть вычислена обратная матрица (А-1), которая при умножении на исходную матрицу А дает единичную (по диагонали расположены единицы, а прочие элементы равны нулю). Для получения обратной матрицы используется функция inv(). Умножение матриц в Matlab производится только с использованием их имен. Описанные действия приведены на рис. 1.2.1-11.
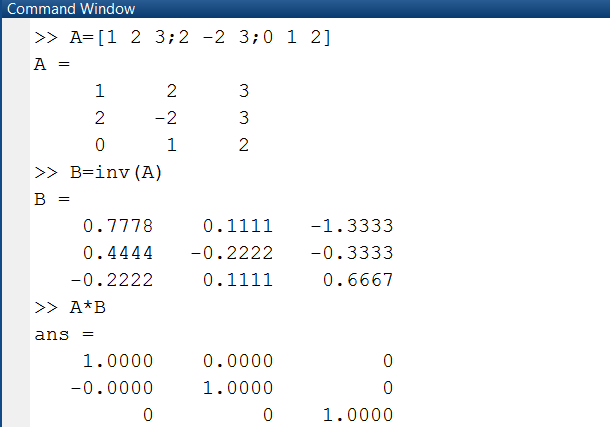
Рис. 1.2.1-11. Получение обратной и единичной матриц
Рассмотрим еще один пример, в котором матрица умножается на скаляр, матрица делится на скаляр и матрица умножается на вектор (рис. 1.2.1-12).
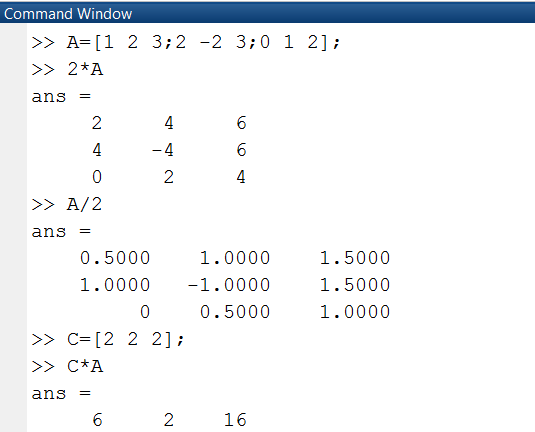
Рис. 1.2.1-12. Действия над матрицами
Вектора и матрицы кроме традиционного их применения для хранения и обработки данных необходимы и для построения графиков функций. При этом вектора используются для построения плоских графиков (графиков функций от одной переменной), а матрицы – для построения трехмерных изображений (графиков функций от двух переменных).
Обратите внимание, что после ввода или формирования элементов векторов и матриц могут возникнуть ошибки. Для контроля и исправления отдельных элементов векторов и матриц можно воспользоваться окном редактора данных (рис. 1.2.1-13).
Окно редактора массива данных (Variables – ИмяПеременной) состоит из панели инструментов и области просмотра значений переменных. В окне редактора данных (рис. 1.2.1-13) можно отображать несколько переменных. Переключение между переменными реализуется с помощью вкладок.
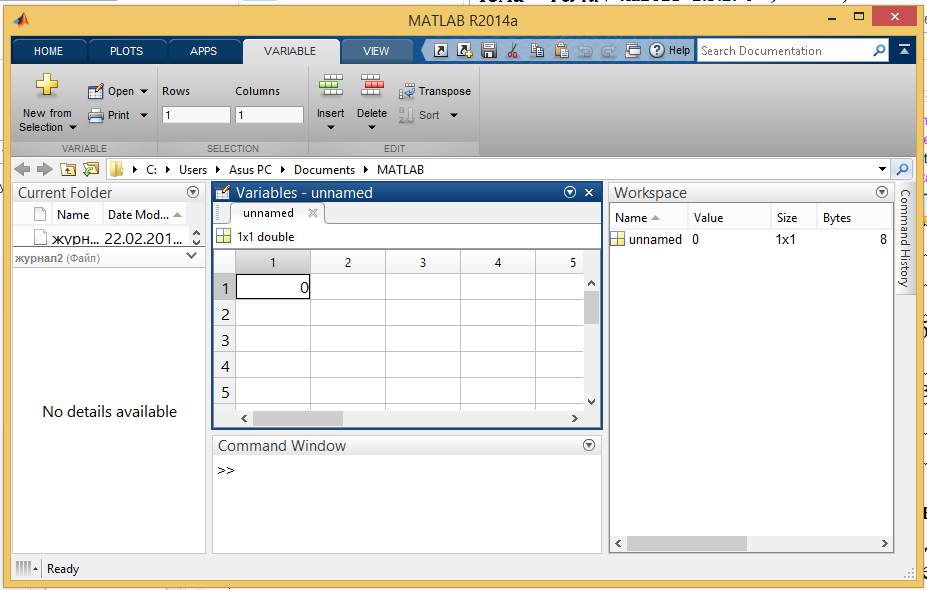
Рис. 1.2.1-13. Окно Рабочей среды с активной инструментальной панелью VARIABLE и открытым Редактором данных
1.2.2. Построение графиков и визуализация вычислений в системе MatLab
Самый простой способ для построения графика функции одной переменной y=f(x) - это предварительное формирование двух векторов одинаковой длины: вектора значений аргументов x и вектора соответствующих им значений функции у, а затем выполнение команды plot(x, y). Выполнение команды plot(x, y) открывает графическое окно и отображает в нем график функции y(x).
Рассмотрим
пример построения графика функции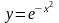 на отрезке [-1.5;1.5] (рис. 1.2.2-1).
на отрезке [-1.5;1.5] (рис. 1.2.2-1).
|
|
Рис.
1.2.2-1. Команды построения графика функции
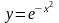
В результате выполнения команды plot(x,y) появляется графическое окно с именем Figure 1 (рис. 1.2.2-2).
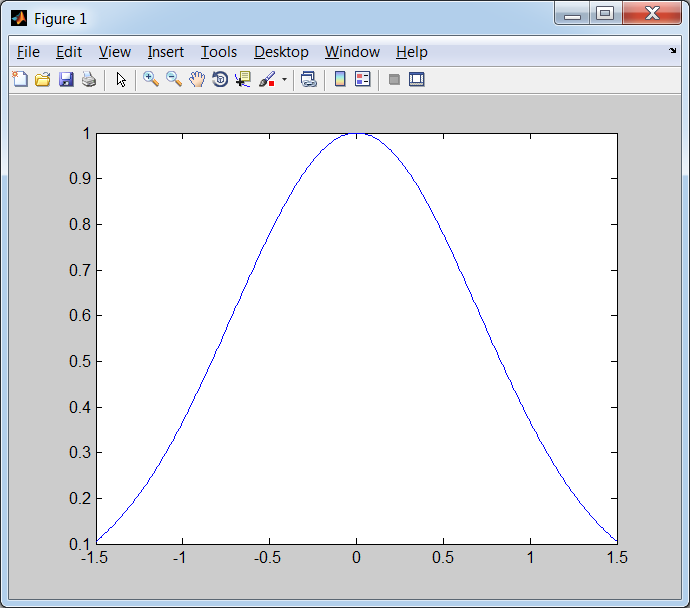
Рис.
1.2.2-2. Графическое окно с изображением
графика
функции
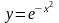
Переход между окнами (от командного окна к графическому окну и обратно) осуществляется с помощью комбинации клавиш <Alt+Tab> или с помощью мыши.
В общем случае, число аргументов у функции plot() не ограничивается двумя. Эта функция имеет следующий формат:
plot(x1,y1,x2,y2,...).
Таким образом, в одном графическом окне можно построить не один, а несколько графиков. Рассмотрим два способа построения в одном графическом окне трех графиков (рис. 1.2.2-3 и рис. 1.2.2-4).
|
|
Рис. 1.2.2-3. Использование векторов значений функций
для построения графиков трех функций
|
|
Рис. 1.2.2-4. Использование матрицы значений функций
для построения графиков трех функций
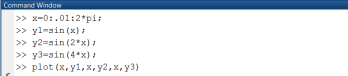
Приведенные в первом и втором примерах наборы команд позволяют получить один и тот же результат (рис. 1.2.2-5.) Разница в том, что в первом примере формируются три вектора значений функций (y1, y2, y3), а во втором – матрица y, содержащая значения функций в виде столбцов.
График, выведенный в графическое окно Matlab, может быть снабжен заголовком, именами осей, дополнительным текстом, сеткой и другой поясняющей информацией. Аргументами команд, управляющими пояснениями, являются текстовые строки. Например, команда title() добавит к графику заголовок. Команда grid on позволяет отобразить координатную сетку. Для вывода подписи осей используются команды Xlabel(), Ylabel().
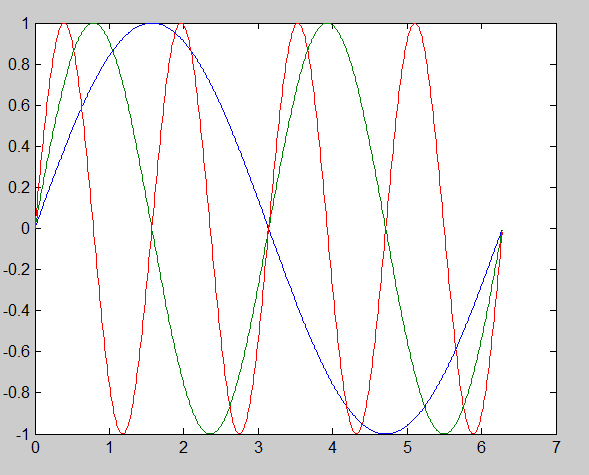
Рис. 1.2.2-5. Графики функций y 1=sin(x); y2=sin(2*x); y3=sin(4*x)
Если в одном графическом окне создаются несколько графиков, полезно с использованием функции legend() отобразить легенду графиков. Ее текстовые аргументы соответствуют подписям соответствующих созданию кривых, а числовой параметр определяет место расположения в графическом окне (табл. 1.2.2-1).
Таблица 1.2.2-1
|
Значение аргумента |
Размещение легенды |
|
-1 |
В правом верхнем углу над областью графика |
|
0 |
Место выбирается автоматически, чтобы не перекрывать область кривых |
|
1 |
В правом верхнем углу (и по умолчанию) |
|
2 |
В левом верхнем углу области графика |
|
3 |
В левом нижнем углу области графика |
|
4 |
В правом нижнем углу области графика |
При выводе в одно графическое окно нескольких графиков удобнее каждый график выводить с использованием своей команды plot(), однако в этом случае происходит создание нового графического окна. Для того чтобы этого избежать, используется команда holdon. Эта команда позволяет расположить все в дальнейшем выводимые графики в одном окне.
При выводе графика можно сменить принятый по умолчанию Matlab цвет и тип точек, с помощью которых рисуется данный график (табл.1.2.2-2). Символы, указывающие на цвет и тип точки, заключаются в апострофы и указываются в команде plot() после имени функции.
Таблица 1.2.2-2
|
Символ |
Цвет |
Символ |
Маркер |
|
y |
желтый |
. |
точка |
|
m |
фиолетовый |
кружок |
: |
|
c |
голубой |
x |
x-метка |
|
r |
красный |
+ |
плюс |
|
g |
зеленый |
* |
звездочка |
|
b |
синий |
s |
квадрат |
|
w |
белый |
d |
алмаз |
|
k |
черный |
v |
треугольник(вниз) |
|
€ |
треугольник (вверх) |
- |
сплошная |
|
< |
треугольник (влево) |
|
точечная |
|
> |
треугольник (вправо) |
-. |
штрих - пунктирная |
|
p |
шестиугольник |
- |
пунктирная |
|
h |
восьмиугольник |
|
|
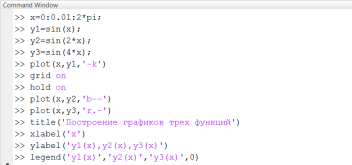
Рассмотрим пример (рис. 1.2.2-6), в котором используются перечисленные выше опции, инструкции и функции. Результат выполнения инструкций, комментирующих графики, приведен на рис. 1.2.2-7.
|
|
Рис. 1.2.2-6. Использование инструкций при построении графиков
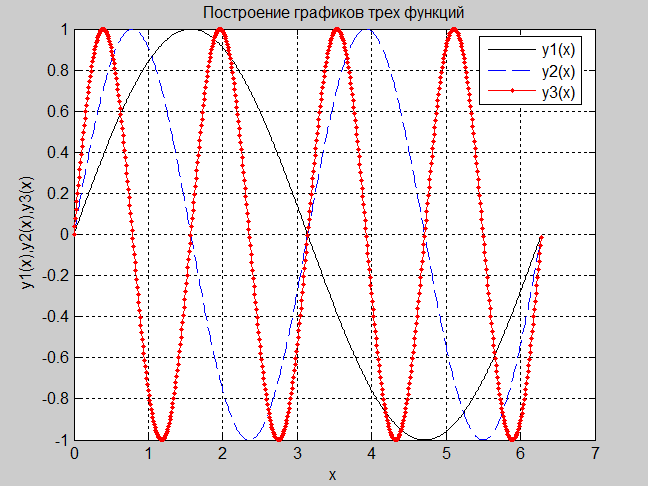
Рис. 1.2.2-7. Результат выполнения инструкций,
комментирующих графики
Большую часть вышеописанных действий можно реализовать также с помощью команд инструментальной панели графических окон (рис. 1.2.1-8).

Рис. 1.2.2-8. Компоненты меню графического окна
Команды основного меню графического окна представляют большой набор средств, предназначенных для отображения и оформления графиков, позволяющих в интерактивном режиме и без использования команд придать графику желаемый вид, а кнопки панели дублируют наиболее часто используемые пункты меню, ускоряя тем самым доступ к ним.
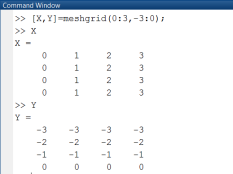
Трехмерные поверхности обычно описываются функцией двух переменных z(x,у). Для построения трехмерных графиков необходимо сформировать два двумерных массива, например, X и Y с использованием функции meshgrid() (рис. 1.2.2-9).
|
|
Рис. 1.2.2-9. Формирование двумерных массивов функцией meshgrid()
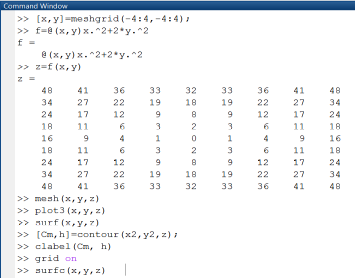
Рис. 1.2.2-10. Построение различных видов графиков
функций двух переменных
Сформированные в виде двумерных массивов данные используются функциями:
-
mesh(X,Y,Z) – построение сетчатого графика;
-
contour(X,Y,Z) – построение графика контурных линий;
-
surf(X,Y,Z) – построения графика сплошной поверхности;
-
surfс(X,Y,Z) – построения графика сплошной поверхности и контурных линий;
-
plot3(X,Y,Z) – построение точек, соединенных отрезками прямых и др.
Рассмотрим
примеры использования перечисленных
выше функций, для чего сформируем матрицу
z(x,y)
с использованием функции f(x,y)
(рис.
1.2.2-10).
Результатом выполнения команды mesh(x,y,z) является построение графика поверхности в виде сетки (рис. 1.2.2-11).
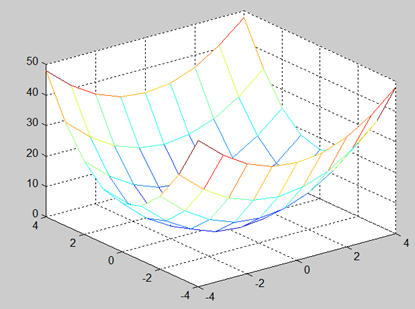
Рис. 1.2.2-11. Результат выполнения команды mesh(x,y,z)
В
результате выполнения команды
plot3(x,y,z)
происходит построение графика
поверхности, где точка соединены
отрезками прямой
(рис. 1.2.2-12).
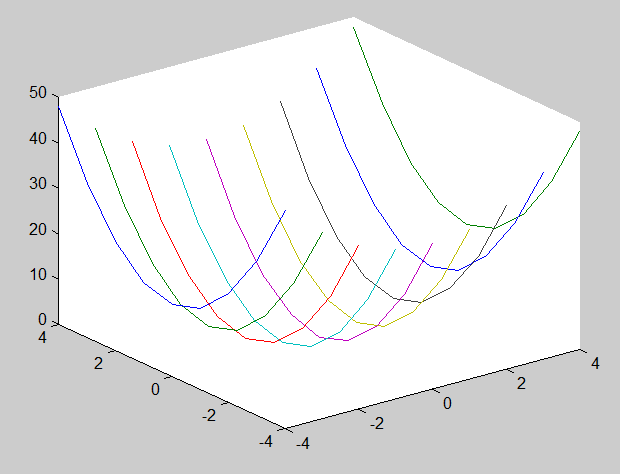
Рис. 1.2.2-12. Результат выполнения команды plot3(x,y,z)
Команда surf(x,y,z) выполняет построение графика сплошной поверхности (рис. 1.2.2-13).
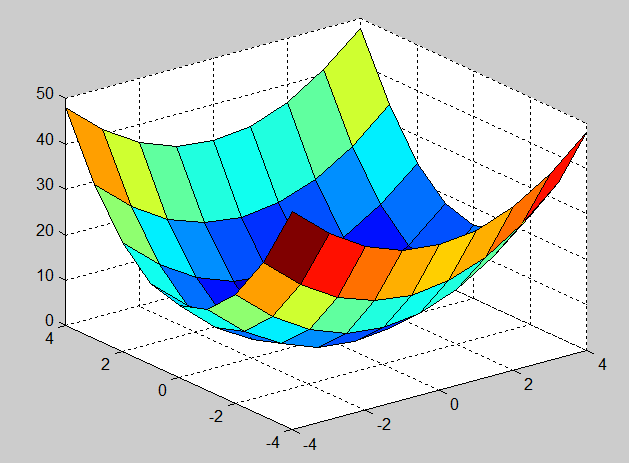
Рис. 1.2.2-13. Результат выполнения команды surf(x,y,z)
Команда contour(x,y,z) позволяет получить график контурных линий (рис. 1.2.2-14).
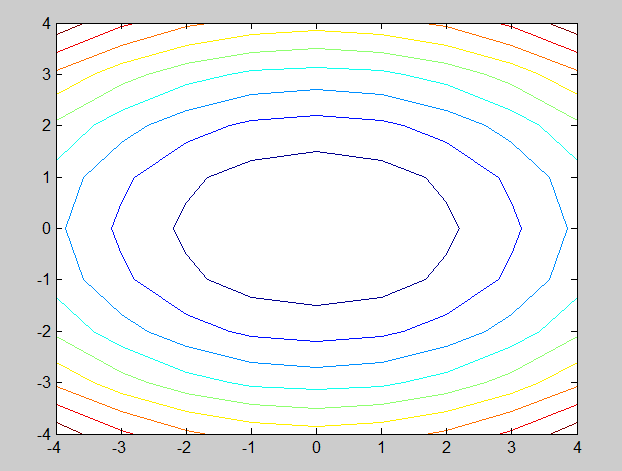
Рис. 1.2.2-14. Результат выполнения команды contour(x,y,z)

Рис. 1.2.2-15
Добавление
команд, представленных на рис. 1.2.2-15,
позволяет нанести на контурные линии
значения функции в отдельных точках
(рис. 1.2.2-16).
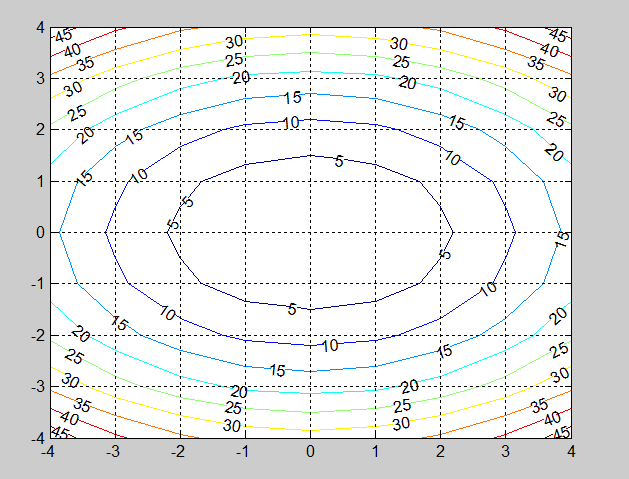
Рис. 1.2.2-16. График контурных линий с
нанесенными значениями функции
Команда surfс(x,y,z) предназначена для построения графика сплошной поверхности, дополненного контурными линиями (рис. 1.2.2-17).
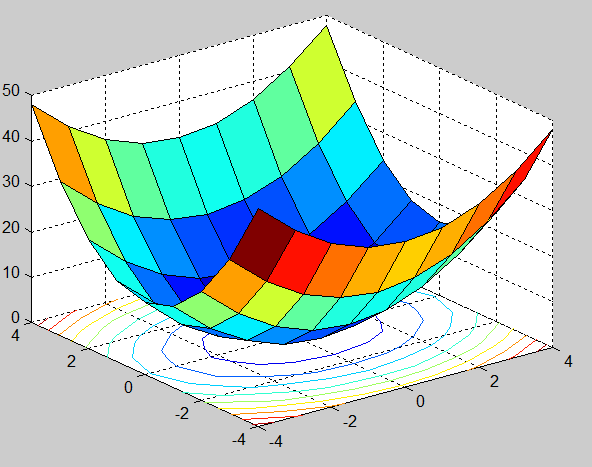
Рис. 1.2.2-17. Результат выполнения команды surfс(x,y,z)