Файл: Matlab Пособие.docx

M-функция возвращает свое значение (или значения) и может быть вызвана из выражений, расположенных в рабочей области или в других программных модулях:

f_name(список_параметров).

По умолчанию все переменные, описанные в теле m-функции, являются локальными, т.е. определены только в пределах функции, в которых они описаны. Между собой m -функции общаются посредством своего имени и входных и выходных параметров. Конструкция

vаri=выражение,

приведенная в общей структуре m-функции, используется, если требуется, чтобы функция возвращала результаты вычислений.

Поскольку m-функция может иметь не один, а несколько выходных параметров, то она во многом напоминает процедуру. Поэтому ее нельзя использовать непосредственно в математических выражениях. Если функция, имеющая несколько выходных параметров, используется как функция, имеющая единственный выходной параметр, то для возврата значения будет использоваться первый из них. Это зачастую ведет к ошибкам в математических вычислениях. Поэтому обращение к m-функции с несколькими выходными параметрами должно иметь вид:

[var1,var2,... ]=f_nаmе(Список_параметров)

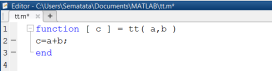
    Создадим простейшую m-функцию с двумя входными и одним выходным аргументами. При активизации Редактора появился шаблон, который заполним следующей информацией (рис. 1.3.3-2).

Рис. 1.3.3-2. Описание m-функции с одним выходным параметром

Сохраним функцию в файле, используя инструмент Save. При этом отметим, что MatLab предлагает в качестве имени m-файла название самой функции, т.е. tt.m. Всегда сохраняйте файл-функцию в m-файле, имя которого совпадает с именем m-функции! Теперь, убедившись, что каталог с файлом tt.m. является текущим, обратимся к функции tt(2, 3) из командной строки (рис. 1.3.3-3).

Рис. 1.3.3-3. Обращение к m-функции tt(a,b)

При вызове m-функции tt(a, b) входные аргументы a и b получили соответственно значения 2 и 3, сумма a и b записана в выходной параметр c, значение выходного аргумента c присвоено переменной y, а результат вывелся в следующую строку командного окна.

Следующий пример показывает создание m-функции с несколькими выходными параметрами. Список выходных параметров в заголовке m-функции заключен в квадратные скобки, а сами параметры отделены запятыми. В качестве примера создадим и выполним m-функцию quadeq(a, b, c), которая по заданным коэффициентам квадратного уравнения находит его корни (рис. 1.3.3-4 , 1.3.3-5).

Рис. 1.3.3-4. Описание функции quadeq(a, b, c)
с двумя выходными параметрами

Рис. 1.3.3-5. Выполнение функции quadeq(a, b, c)
с двумя выходными параметрами

Иногда и при создании m-функций желательно применение глобальных переменных (например, если параметров слишком много). В таких случаях используемые глобальные переменные надо объявить командой:

global varl, var2,...

Для того чтобы несколько функций могли совместно использовать глобальные переменные, они должны быть объявлены как global в каждом из модулей.

4. Алгоритмические операторы Matlab

Помимо программ с линейной структурой, инструкции которых исполняются строго по порядку, существует множество алгоритмов, структура которых нелинейная. При этом последовательность элементов алгоритмов может выполняться в зависимости от определенных условий, иногда с конечным числом повторений – регулярных циклов, иногда в виде циклов, завершаемых при выполнении заданного условия. Практически любая серьезная программа имеет нелинейную структуру. Для создания таких программ необходимы специальные управляющие структуры. Они имеются в любом языке программирования высокого уровня, и в частности в Matlab.

  Рассмотрим операторы m-файлов подробнее.

Оператор присваивания. Основным оператором системы программирования MatLab является оператор присваивания, имеющий следующую структуру:

ИмяПеременной = выражение

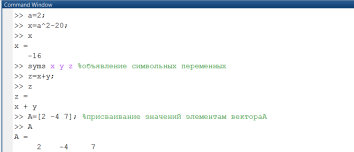
Оператор предназначен для идентификации переменных и обозначается символом =, слева от которого находится имя переменной, а справа арифметическое или строковое выражение (правила записи арифметических и строковых выражений были рассмотрены в п. 1.1.2). Приведем несколько примеров операторов присваивания (рис. 1.3.4-1).

Рис. 1.3.4-1. Примеры операторов присваивания

Все переменные, используемые в правой части оператора присваивания, должны быть предварительно определены. Если командная строка заканчивается символом точка с запятой (;), то результат выполнения оператора не выводится, иначе он выводится в следующей строке командного окна. Это замечание распространяется и на выполнение операторов присваивания, расположенных в m-файлах.

Операторы ввода данных. Ввод данных в Matlab может осуществляться как с использованием оператора присваивания (a=5;), так и с использованием функции ввода данных с клавиатуры:

ИмяПеременной = input ('Запроc');

Эта функция вводит выражение с клавиатуры, а результат заносится в переменную с именем a. В приведенном ниже примере в переменную a введено вначале числовое значение, а затем числовое выражение (рис. 1.3.4-2).

Рис. 1.3.4-2. Ввод данных с клавиатуры

Функция input() может использоваться и для ввода произвольных строковых выражений. При этом она задается в следующем виде:

input('Запроc', V);

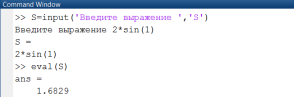
При выполнении этой функции вычисления останавливаются в ожидании ввода строкового выражения. Введенное выражение выводится в следующей строке. Для вычисления выражения, заданного в символьном виде, использована функция eval(). Это иллюстрирует пример на рис. 1.3.4-3.

Рис. 1.3.4-3. Вычисление выражения, заданного в символьном виде

Условный оператор if…end. Условный оператор if в общем виде записывается следующим образом:

if ЛогическоеВыражение1 

Инструкции1

elself Условие2 

ЛогическоеВыражение2 

else 

ЛогическоеВыражение3 

end

Правила записи логических выражений описано в Теме 1.1.

Эта конструкция допускает несколько частных вариантов. Простейшее – усеченное разветвление [x] имеет следующий вид:

if ЛогическоеВыражение

Инструкции

end

Напомним, что если ЛогическоеВыражение возвращает логическое значение 1 (то есть «Истина»), выполняются Инструкции, составляющие тело структуры if...end. При этом оператор end указывает на конец перечня инструкций. Инструкции в списке разделяют запятая или точка с запятой. Если ЛогическоеВыражение не выполняется (дает логическое значение 0, «Ложь»), то Инструкции также не выполняются.

Ниже приведен пример использования простейшего усеченного разветвления, реализованного с использования оператора if (рис. 1.3.4-4).

Рис. 1.3.4-4. Пример усеченного разветвления

Вторая частная конструкция напоминает стандартное разветвление [x]:

if ЛогическоеВыражение 

Инструкции1 

else 

Инструкции2 

end

Здесь выполняются Инструкции1, если выполняется истинно
ЛогическоеВыражение, или, в противном случае, выполняются
Инструкции2.

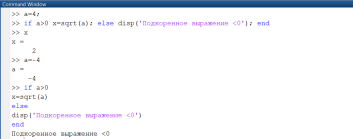
В примере, приведенном на рис. 1.3.4-5, рассматривается стандартное разветвление, реализованное с использованием оператора if.

Рис. 1.3.4-5. Пример стандартного разветвления

Из приведенного примера видно, что оператор if может быть как в одну строку, так и в несколько строк.

Рассмотрим пример более сложного - вложенного разветвления. Рассмотрим пример

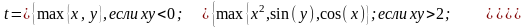
причем, для того чтобы полностью отразить структуру сложного разветвления, не заботясь о переносе длинных командных строк, используем m-функцию (рис. 1.3.4-7). Подберем данные для проверки основного разветвления и обратимся к функции raz() с различными исходными данными (рис. 1.3.4-6).

Рис. 1.3.4-6. Обращение к функции raz() с различными исходными данными

Рис. 1.3.4-7. Функция, реализующая вложенное разветвление

Оператор множественного выбора – switch. Для осуществления множественного выбора используется следующая конструкция switch:

switch Bыражение

case Зачение_1

Список_инструкций_1

case Значение_2

Список_инструкций_2

…

case Значение_N

Список_инструкций_N

otherwise

Список_инструкций_N+1

end

Если выражение после заголовка switch имеет значение одного из выражений Значение..., то выполняется блок операторов case, в противном случае — список инструкций после оператора otherwise. При выполнении блока case исполняются те списки инструкций, для которых Значение совпадает с Bыpaжением. Обратите внимание на то, что Значение может быть числом, константой, переменной, вектором ячеек или даже строчной переменной. Поясним использования оператора перебора switch следующим примером:

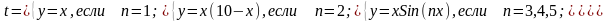
M-функция, реализующая множественное разветвление, приведена на рис. 1.3.4-8, а обращение к ней при исходных данных, позволяющих проверить каждую ветвь разветвления, показано на рис. 1.3.4-9.

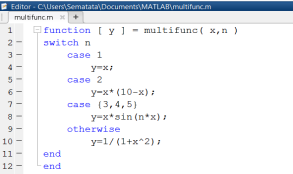
Рис. 1.3.4-8. Функция, реализующая множественное разветвление

Рис. 1.3.4-9. Обращения к функции multifunc()

У функции multifunc(x,n) два параметра, причем второй играет роль индикатора, определяющего тип функциональной зависимости. Значение функции записывается в переменную y. Если n=1, то выполняется первый case-блок, если 2, то – второй, если n=2, 3 или 4, то – третий. Если же значение переменной n не совпадает ни с одним из перечисленных значений, то выполняется команда, расположенная после ключевого слова otherwise.

  Оператор регулярного цикла – for...end. Оператор цикла типа for...end обычно используется для организации вычислений с заданным числом повторений циклов. Конструкция такого цикла имеет следующий вид:

for vаг = s:d:e

Инструкция1

….

ИнструкцияN

end

где s - начальное значение переменной цикла var, d - приращение этой переменной и е - конечное значение управляющей переменной, при превышении которого цикл завершается. Возможна и запись в виде s:е (в этом случае d=l). Список выполняемых в цикле инструкций завершается оператором end.

В качестве примера использования оператора for...end вычислим сумму элементов массива х, значения которого определены в командном окне с использованием m-функции summa() (рис. 1.3.4-10), параметром которой служит вектор x. Количество элементов массива х определяется функцией length. Кроме обращения к функции в командном окне предусмотрена проверка результата вычислений с использованием встроенной функции sum(x) (рис. 1.3.4-11).

Рис. 1.3.4-10. Функция, вычисляющая сумму элементов массива

Рис. 1.3.4-11. Обращение к функции summa() и встроенной функции sum()

В цикле может быть использован оператор continue, который передает управление в следующую итерацию цикла, пропуская операторы, которые записаны за ним, причем во вложенном цикле он передает управление на следующую итерацию основного цикла. Оператор break может использоваться для досрочного прерывания выполнения цикла (например, при отладке участка программы). Как только он встречается в программе, цикл прерывается.

Кроме простых регулярных циклов в Matlab имеется возможность организации вложенных циклов. Рассмотрим пример формирования двумерного массива а, каждый элемент которого представляет сумму его индексов (рис. 1.3.4-12). Обращение к script-файлу vzikl приведено на рис. 1.3.4-13.

Рис. 1.3.4-12. Script-файл, иллюстрирующий вложенные циклы

Рис. 1.3.4-13. Обращение к script-файлу с именем vzikl

Оператор итеративного цикла – while…end. Общий вид структуры while…end выглядит следующим образом:

while ЛогическоеВыражение

Инструкции

end

Отличительной особенностью этой структуры является то, что инструкции, расположенные в теле структуры повторения, выполняются только в том случае, если некоторое ЛогическоеВыражение «истинно». Как только условие становится «ложным», происходит выход из структуры повторения, и управление передается на инструкцию, расположенную после ключевого слова end.

Приведем простой пример (рис. 1.3.4-14).

Рис. 1.3.4-14. Диалоговая программа, использующая оператор while…end

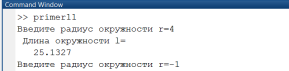
Эта программа, сохраненная в m-файле с именем primer11, служит для многократного вычисления длины окружности по вводимому пользователем значению радиуса r, где диалог реализован с помощью команды input. Cтроки, связанные с вводом переменной r и вычислением длины окружности, включены в управляющую структуру while...end. Это необходимо для циклического повторения вычислений при вводе различных значений r. Пока r>=0, цикл повторяется. Но стоит задать r<0, вычисление длины окружности перестает выполняться, а цикл завершается. Поскольку во второй строке программы величина r определена равной 0, цикл повторяется хотя бы один раз.

Работа с программой в командном окне представлена на рис. 1.3.4-15.

Рис. 1.3.4-15. Обращения к программе вычисления длины окружности

В управляющих структурах, в частности в циклах for и while, часто используются операторы, влияющие на их выполнение. Так, оператор break может использоваться для досрочного прерывания выполнения цикла. Как только он встречается в программе, цикл прерывается.

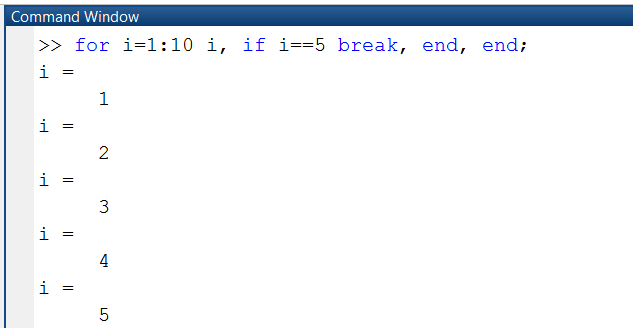
Рассмотрим пример досрочного прерывания цикла при выполнении условия i=5 (рис. 1.3.4-16).

Рис. 1.3.4-16. Прерывание программы с применением оператора break

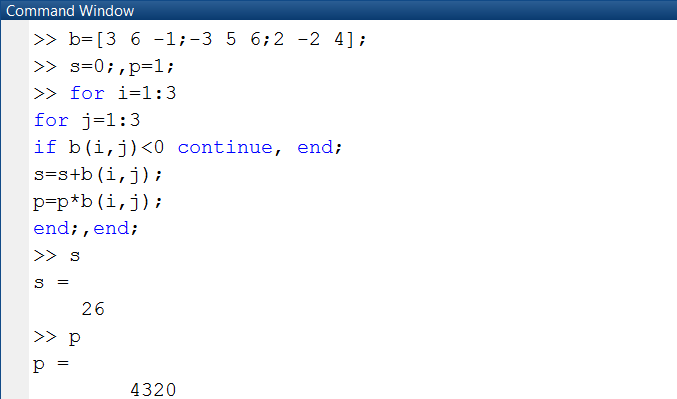
Оператор continue передает управление в следующую итерацию цикла, про­пуская операторы, которые записаны за ним, причем во вложенном цикле он пере­дает управление на следующую итерацию основного цикла. Ниже приведен пример вычисления суммы и произведения положительных элементов двумерного массива b(3,3) (рис. 1.3.4-17).

Рис. 1.3.4-17. Прерывание программы с применением оператора continue

5. Примеры решения задач с использованием

m-файлов

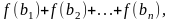Пример 1.3.5-1. Даны n чисел . Требуется вычислить их сумму: где

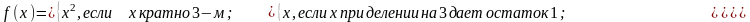
Для решения поставленной задачи разработана функция fb(x), реализующая алгоритм вычисления текущего значения функции. Функция имеет один входной параметр – текущее значение элемента массива b и один выходной параметр – y (рис. 1.3.5-1). Обращение к функции происходит в цикле, организованном для вычисления суммы (рис. 1.3.5-2).

Рис. 1.3.5-1. Функция, реализующая алгоритм Примера 1.3.5-1

Рис. 1.3.5-2. Программа, реализующая вычисление суммы чисел

Для вычисления суммы значений функции создан script-файл с именем zadashа.m, в котором сначала заданы количество чисел (n=10) и вектор их значений (b), а затем организован регулярный цикл для обращения в функции fb() и вычисления суммы.

Вычисления производятся запуском script-файла путем набора в командной строке окна Command Window его имени zadasha. Результаты его выполнения выведены на рис. 1.3.5-3.

Рис. 1.3.5-3. Запуск script-файла zadasha на выполнение

Пример 1.3.5-2. Сформировать из произвольных чисел двумерный массив а(3,4). Вычислить и вывести одномерный массив b, каждый элемент которого есть среднее арифметическое элементов соответствующей строки массива а[].