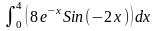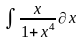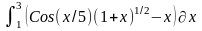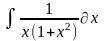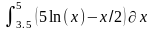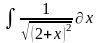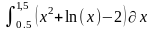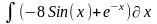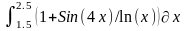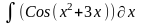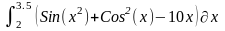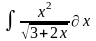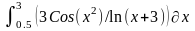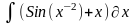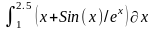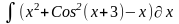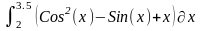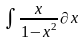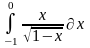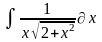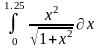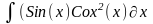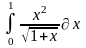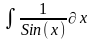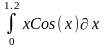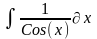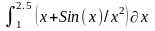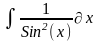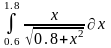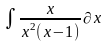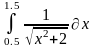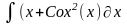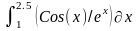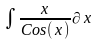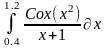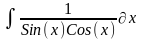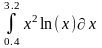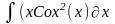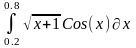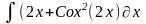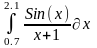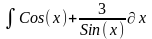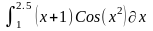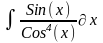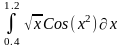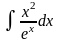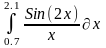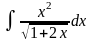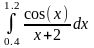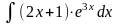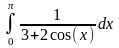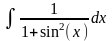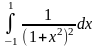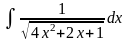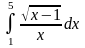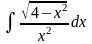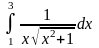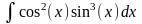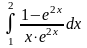ВУЗ: Московский технический университет связи и информатики
Категория: Учебное пособие
Дисциплина: Программирование
Добавлен: 23.10.2018
Просмотров: 6244
Скачиваний: 74
СОДЕРЖАНИЕ
Раздел 1. Основы работы с математическим пакетом Matlab
Тема 1.1. Элементы рабочей среды Matlab
1.1.1.Элементы рабочей среды Matlab и простейшие вычисления
1.1.2. Основные объекты системы Matlab
1.1.3. Лабораторная работа по теме «Элементы рабочей среды Matlab и простейшие вычисления»
1.2.2. Построение графиков и визуализация вычислений в системе MatLab
1.2.3. Лабораторная работа по теме
«Векторы, матрицы и построение графиков
1.2.4. Контрольные вопросы по теме
Тема 1.3. Средства Matlab для создания и описания m-файлов
Пример 1.3.5-1. Даны n чисел . Требуется вычислить их сумму: где
1.3.6. Лабораторная работа по теме
«Средства алгоритмизации и программирования
1.3.7. Контрольные вопросы по теме
Раздел 2. Технология решения вычислительных задач средствами MatLab
Тема 2.1. Решение нелинейных уравнений
2.1.2. Лабораторная работа по теме
«Технология решения нелинейных уравнений средствами пакета MatLab»
1. Вопросы, подлежащие изучению
2.1.3. Контрольные вопросы по теме
Тема 2.2. Технология аппроксимации интерполяции функций в среде пакета MatLab
Рис. 2.2.1-5. Вычисление функции в точке х=0.58
Рис. 2.2.2-7. Графики интерполирующих функций
Тема 2.4. Технология решения обыкновенных дифференциальных уравнений
Рис. 2.4.1-2. Решение ОДУ методом Рунге-Кутты четвертого порядка
1. Вопросы, подлежащие изучению
Тема 2.5. Технология решения задач одномерной оптимизации
2.5.2. Лабораторная работа по теме
«Технология решения задач одномерной оптимизации»
1. Вопросы, подлежащие изучению
3. Варианты индивидуальных заданий
2.5.3. Контрольные вопросы по теме
Тема 2.6. Технология решения задач многомерной оптимизации
Тема
2.3. Технология интегрирования
в
среде MatLab
2.3.1. Вычисление неопределенных и определенных интегралов
2.3.2. Лабораторная работа по теме «Технология интегрирования
в среде MatLab»
2.3.3. Контрольные вопросы по теме
2.3.1.
Вычисление неопределенных и
определенных
интегралов
При вычислении определенных интегралов первообразную функцию F(x) не всегда удается выразить аналитически, а кроме того иногда подынтегральная функция f(x) задана в виде таблицы (xi и yi, где i = 1, 2, …, n). Это приводит к необходимости использования численных методов интегрирования.
Существует ряд методов численного интегрирования. Во всех этих методах вычисление осуществляется по приближенным формулам, называемым квадратурами.
Суть получения формул численного интегрирования состоит в том, что на элементарных отрезках интегрирования подынтегральную функцию заменяют простейшим интерполяционным полиномом, который легко может быть проинтегрирован в аналитическом виде. Так, например, для получения формул прямоугольников, трапеций и Симпсона используют полиномы соответственно нулевой, первой и второй степени.
Формулы прямоугольников:
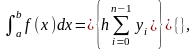
где:
h – шаг интегрирования;
yi – значение подынтегральной функции от аргумента xi, k=0, 1, …,n;
n – число разбиений интервала интегрирования a, b.
Формула трапеций:
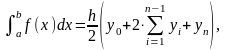
где:
h – шаг интегрирования;
y0 – значение подынтегральной функции при х = a;
yn – значение подынтегральной функции при х = b;
Формула Симпсона:
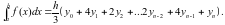
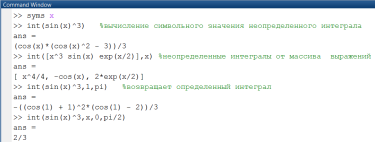
Для символьного вычисления неопределенных и определенных интегралов используется функция Matlab int(), которая может иметь один из следующих форматов:
-
int(S) – возвращает символьное значение неопределенного интеграла от символьного выражения или массива символьных выражений S по переменной, которая автоматически определяется функцией findsym(). Если S – скаляр или матрица, то вычисляется интеграл по переменной 'х'.
-
int(S, v) – возвращает неопределенный интеграл от S по символьной переменной v.
-
int(S, a, b) – возвращает определенный интеграл от S с пределами интегрирования от а до b, причем пределы интегрирования могут быть как символьными, так и числовыми.
-
int(S, v, a, b) – возвращает определенный интеграл от S по переменной v с пределами от а до b.
Ниже
приведены примеры использования функции
Matlabint()
(рис.
2.3.1-1).
|
|
Рис. 2.3.1-1. Примеры вычисления интегралов
В системе MatLab функции вычисления интегралов используют численные методы трапеции, Симпсона и некоторые другие. Рассмотрим технологию интегрирования с использованием некоторых функций.
Для
вычисления интеграла по формуле
трапеции в
MatLab используется функция trapz(x,y).
Эта функция возвращает значение интеграла
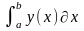 от функции
y(x),
которая может быть представлена вектором
или матрицей. Если y(x)
– матрица, то функция возвращает вектор
значений интеграла каждого столбца
матрицы. Если вектор узлов не задан -
trapz(y),
то в качестве ординат x
используются
индексы вектора y(x=1:length(y)),
где функция определяет длину вектора
y.
Важно, что узлы по оси x
могут быть как равноотстоящими, так и
неравноотстоящими.
от функции
y(x),
которая может быть представлена вектором
или матрицей. Если y(x)
– матрица, то функция возвращает вектор
значений интеграла каждого столбца
матрицы. Если вектор узлов не задан -
trapz(y),
то в качестве ординат x
используются
индексы вектора y(x=1:length(y)),
где функция определяет длину вектора
y.
Важно, что узлы по оси x
могут быть как равноотстоящими, так и
неравноотстоящими.
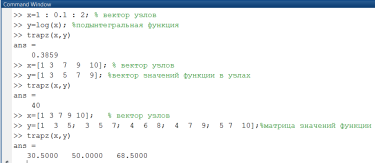
Рассмотрим несколько примеров вычисления значений определенных интегралов методом трапеций при различных способах задания узлов подынтегральной функции (рис. 2.3.1-2).
|
|
Рис. 2.3.1-2. Вычисление определенных интегралов с использованием
ФункцииMatlab trapz()
Для вычисления интеграла по формуле Симпсона в MatLab применяется функция quad(). При обращении к этой функции шаг интегрирования не задается, а используется параметр – требуемая точность вычисления интеграла.
Минимальная форма обращения к функции – q=quad('f',a,b), где f – имя функции, взятое в одинарные кавычки, второй и третий аргументы – пределы интегрирования.
|
|
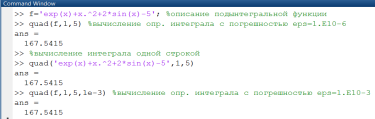
Рис.
2.3.1-3. Вычисление определенных интегралов
с
использованием функции quad()
Допускается задание четвертого входного параметра eps – абсолютной погрешности: q=quad('f', a, b, eps). По умолчанию eps =10-6.
Рассмотрим
примеры вычисления определенного
интеграла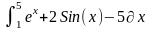 с
использованием функции Matlab
quad() (рис.
2.3.1-3).
с
использованием функции Matlab
quad() (рис.
2.3.1-3).
2.3.2. Лабораторная работа по теме
«Технология интегрирования в среде Matlab»
-
Вопросы, подлежащие изучению
-
Получение символьного выражения неопределенного интеграла средствами пакета Matlab.
-
Вычисление значения определенного интеграла с использованием функций.
-
Вычисление значения определенного интеграла с использованием функций Matlab int(), trapz(), quad().
-
Формулы численного интегрирования: средних прямоугольников, трапеций и Симпсона.
-
Общее задание
-
Изучите материал Темы 2.3 (п. 2.3.1).
-
Выберите из табл. 2.3.2-1 вариант индивидуального задания.
-
Получить символьное выражение неопределенного интеграла с использованием функций int(S) и int(S, x), где S – символьное выражение, а х - переменная.
-
Вычислите значение определенного интеграла с использованием функции int() формата int(S,a,b), где a, b – пределы интегрирования.
-
Вычислите определенный интеграл с использованием функции Matlab, реализующей формулу трапеций, - trapz(x, y), предварительно получив таблицу значений подынтегральной функции с шагом h и задав значения аргумента и функции в виде векторов.
-
Вычислите значение определенного интеграла с использованием функции Matlab, реализующей формулу Симпсона, – quad('f',a,b), где f – имя функции, взятое в одинарные кавычки.
-
Представьте результаты работы преподавателю, ответьте на поставленные вопросы.
-
Выполните команду clear all.
-
Оформите отчет по выполненной работе.
-
Варианты индивидуальных заданий
Таблица 2.3.2-1
|
№ |
Интеграл 1 |
Интеграл 2 |
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
|
11 |
|
|
|
12 |
|
|
|
13 |
|
|
|
14 |
|
|
|
15 |
|
|
|
16 |
|
|
|
17 |
|
|
|
18 |
|
|
|
19 |
|
|
|
20 |
|
|
|
21 |
|
|
|
22 |
|
|
|
23 |
|
|
|
24 |
|
|
|
25 |
|
|
|
26 |
|
|
|
27 |
|
|
|
28 |
|
|
|
29 |
|
|
|
30 |
|
|
-
Содержание отчета
-
В форме комментариев:
-
Название лабораторной работы
-
ФИО студента, номер группы
-
№ варианта
-
Индивидуальное задание
-
Протокол вычислений (сессии) в окне Command Window, снабженный необходимыми комментариями.
2.3.3. Контрольные вопросы по теме
1) Какой функцией в Matlab определяется символьное значение определенного интеграла?
2) Назначение функции trap(x,y).
-
Что возвращает функция trap(x,y), если y(x) – матрица?
-
Можно ли использовать функцию trap(x,y), если узлы по оси х - не равноотстоящие?
-
Какая функция Matlab позволяет вычислить определенный интеграл с заданной точностью?
-
Способы задания подынтегральной функции при вычислении определенного интеграла с использованием функции quad().
-
Какова точность вычисления определенного интеграла по умолчанию?
Тема 2.4. Технология
решения обыкновенных
дифференциальных
уравнений
2.4.1. Численное решение обыкновенных дифференциальных уравнений
2.4.2. Лабораторная работа по теме
2.4.3. Контрольные вопросы по теме
2.4.1.
Численное решение обыкновенных
дифференциальных уравнений
Представим
обыкновенное дифференциальное уравнение
(ОДУ) первого порядка в виде, разрешенном
относительно производной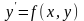 ,
и пусть
,
и пусть
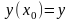 –
начальные условия его решения.
–
начальные условия его решения.
Тогда
решением ОДУ является функция
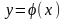 ,
которая, будучи подставленной в исходное
уравнение, обратит его в тождество, и
одновременно будут выполняться начальные
условия. Эта задача в математике
называется задачей
Коши.
,
которая, будучи подставленной в исходное
уравнение, обратит его в тождество, и
одновременно будут выполняться начальные
условия. Эта задача в математике
называется задачей
Коши.
Задача
Коши при решении ОДУ n-го
порядка
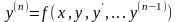 формулируется
аналогично, при этом начальными условиями
должны быть:
формулируется
аналогично, при этом начальными условиями
должны быть:
 При
решении ОДУ n-го
порядка уравнение путем выполнения
ряда обозначений
При
решении ОДУ n-го
порядка уравнение путем выполнения
ряда обозначений
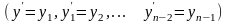 представляется
в виде системы дифференциальных
уравнений:
представляется
в виде системы дифференциальных
уравнений:

Результатом решения ОДУ численными методами является таблица значений y = (x) на некотором множестве значений аргументов. Поэтому при постановке задачи численного решения ОДУ наряду с начальными условиями x0, y0 необходимо задать область решения – отрезок [a;b] и шаг изменения аргумента h (шаг интегрирования).
Для получения численного решения ОДУ используются методы Рунге-Кутты [1]. Методы различаются порядком. Чем выше порядок метода, тем точнее решение, полученное при равном шаге интегрирования.
В Matlab имеется несколько функций для решения задачи Коши. Рассмотрим две функции, используемые для решения обыкновенных дифференциальных уравнений (ОДУ): ode23() – использует метод Рунге-Кутты второго и третьего порядка; ode45() – использует метод Рунге-Кутты четвёртого и пятого порядка точности с автоматическим выбором шага.
В MatLab обращением к функциям, предназначенным для решения ОДУ, является:
[x, y] = ode23('fun',t0,tf,x0)
[x, y] = ode45('fun',t0,tf,x0)
Входными параметрами функций являются:
-
'fun' – имя функции (в виде строчной переменной) или ссылка на функцию, задающую правую часть дифференциального уравнения (уравнение должно быть записано в нормальной форме
y' = fun(x,y)); -
t0 – начальное значение аргумента;
-
tf – конечное значение аргумента;
-
х0 – вектор начальных условий.
Выходными параметрами функций являются:
-
x – вектор, содержащий отсчёты аргумента в точках решения;
-
y – вектор, содержащий вычисленные значения результата решения ОДУ в точках, соответствующих отсчетам независимой перемен-ной x.
Требования к точности и другие параметры численного решения задаются в Matlab по умолчанию. Изменить эти настройки позволяет дополнительный аргумент OPTIONS.
|
|
Рис. 2.4.1-1. Решение ОДУ методом Рунге-Кутты второго порядка
Рассмотрим
примеры использования функций ode23()
и ode45() для
решения ОДУ вида:
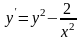 на отрезке [1;10]
с шагом интегрирования 1 при начальных
условиях y(1)=1.
Решение ОДУ с использованием функции
ode23()
приведено
на рис. 2.4.1-1.
на отрезке [1;10]
с шагом интегрирования 1 при начальных
условиях y(1)=1.
Решение ОДУ с использованием функции
ode23()
приведено
на рис. 2.4.1-1.
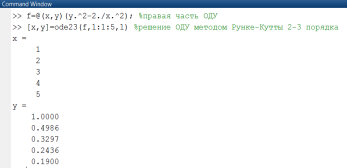
На рис. 2.4.1-2 приведено решение того же ОДУ, но с использованием функции ode45(). Вывод таблицы решения дополнен графиком функции y(x) (рис. 2.4.1-3).
|
|
Рис. 2.4.1-2. Решение ОДУ методом Рунге-Кутты четвертого порядка
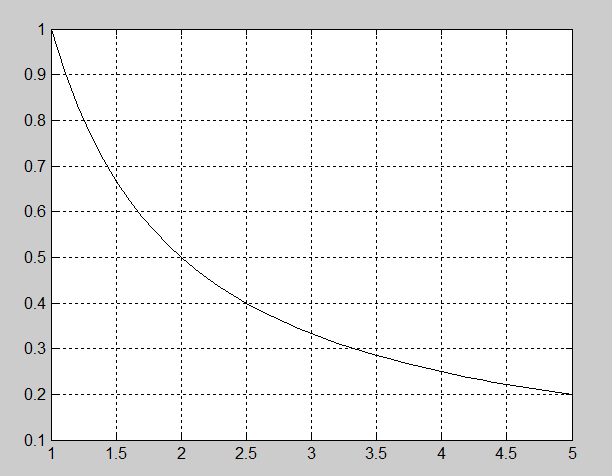
Рис. 2.4.1-3. Графическое решение ОДУ
При решении ОДУ высокого порядка вводят обозначения (новые функции) для всех производных, кроме самой старшей. В этих обозначениях самая старшая производная становится записанной, как первая. Исходное уравнение дополняется тождествами, определяющими правила введения новых функций. Проиллюстрируем описанный подход при решении ОДУ второго порядка.
Требуется
решить
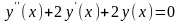 с начальными условиями: и
с начальными условиями: и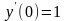 .
Сведем заданное ОДУ к равноценной
системе ОДУ первого порядка. Для этого
переобозначим функцию
.
Сведем заданное ОДУ к равноценной
системе ОДУ первого порядка. Для этого
переобозначим функцию
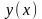 ,
как
,
как
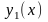 ,
и введем функцию
,
и введем функцию
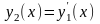 .
Запишем исходное уравнение в новых
обозначениях:
.
Запишем исходное уравнение в новых
обозначениях:
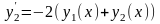 (здесь
учтено, что
(здесь
учтено, что
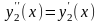 ).
Дополним это уравнение тождеством
).
Дополним это уравнение тождеством
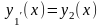 и получим нужную систему ОДУ. Эту систему
следует дополнить начальными условиями:
и получим нужную систему ОДУ. Эту систему
следует дополнить начальными условиями:
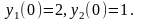
Решение системы ОДУ в Matlab начинается с определения векторной функции (рис. 2.4.1-4).
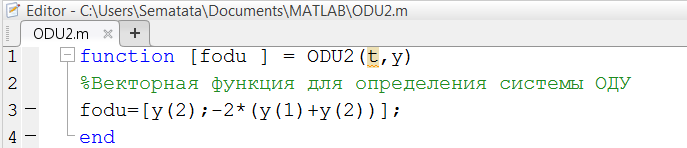
Рис. 2.4.1-4. Определение векторной функции
Для решения дифференциального уравнения (системы уравнений) используем команды, где решение системы ОДУ записывается в переменную y. При этом элемент y(1) содержит значение функции y(x), а y(2) значение производной y'(x). Команда plot(x, y) строит график функции решения ОДУ и ее производной (рис. 2.4.1-6).
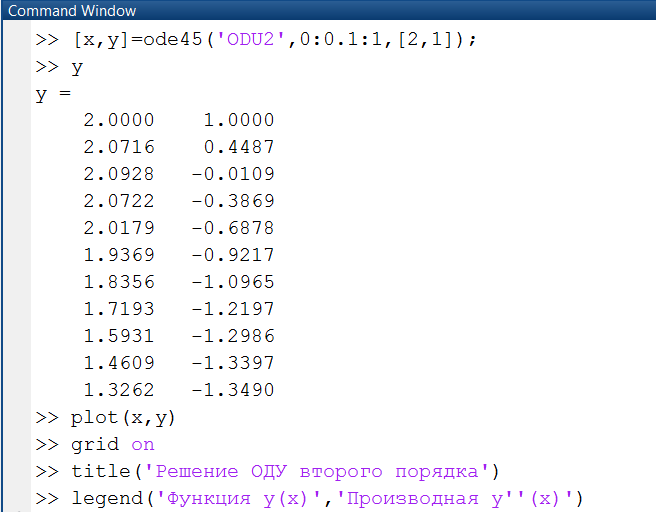
Рис. 2.4.1-5. Решение ОДУ второго порядка
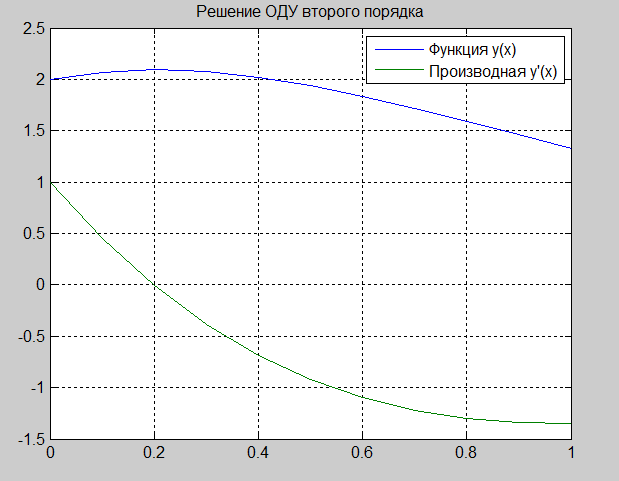
Рис. 2.4.1-6. Графики функций решения ОДУ и производной