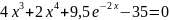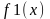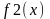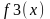ВУЗ: Московский технический университет связи и информатики
Категория: Учебное пособие
Дисциплина: Программирование
Добавлен: 23.10.2018
Просмотров: 6253
Скачиваний: 74
СОДЕРЖАНИЕ
Раздел 1. Основы работы с математическим пакетом Matlab
Тема 1.1. Элементы рабочей среды Matlab
1.1.1.Элементы рабочей среды Matlab и простейшие вычисления
1.1.2. Основные объекты системы Matlab
1.1.3. Лабораторная работа по теме «Элементы рабочей среды Matlab и простейшие вычисления»
1.2.2. Построение графиков и визуализация вычислений в системе MatLab
1.2.3. Лабораторная работа по теме
«Векторы, матрицы и построение графиков
1.2.4. Контрольные вопросы по теме
Тема 1.3. Средства Matlab для создания и описания m-файлов
Пример 1.3.5-1. Даны n чисел . Требуется вычислить их сумму: где
1.3.6. Лабораторная работа по теме
«Средства алгоритмизации и программирования
1.3.7. Контрольные вопросы по теме
Раздел 2. Технология решения вычислительных задач средствами MatLab
Тема 2.1. Решение нелинейных уравнений
2.1.2. Лабораторная работа по теме
«Технология решения нелинейных уравнений средствами пакета MatLab»
1. Вопросы, подлежащие изучению
2.1.3. Контрольные вопросы по теме
Тема 2.2. Технология аппроксимации интерполяции функций в среде пакета MatLab
Рис. 2.2.1-5. Вычисление функции в точке х=0.58
Рис. 2.2.2-7. Графики интерполирующих функций
Тема 2.4. Технология решения обыкновенных дифференциальных уравнений
Рис. 2.4.1-2. Решение ОДУ методом Рунге-Кутты четвертого порядка
1. Вопросы, подлежащие изучению
Тема 2.5. Технология решения задач одномерной оптимизации
2.5.2. Лабораторная работа по теме
«Технология решения задач одномерной оптимизации»
1. Вопросы, подлежащие изучению
3. Варианты индивидуальных заданий
2.5.3. Контрольные вопросы по теме
Тема 2.6. Технология решения задач многомерной оптимизации
«Технология решения
нелинейных уравнений
средствами
пакета MatLab»
1. Вопросы, подлежащие изучению
-
Задание функций и их производных с использованием средств пакета Matlab.
-
Получение таблиц значений функций в заданных границах изменения аргумента.
-
Построение графиков функций средствами Matlab.
-
Этапы решения нелинейных уравнений: отделение и уточнение корня.
-
Решение нелинейных уравнений с использованием встроенных функций пакета Matlab: fzero() и solve().
2. Общее задание
-
Изучите материал Темы 2.1 (п. 2.1.1).
-
Выберите индивидуальный вариант задания из табл. 2.1.2-1.
-
Отделите корень нелинейного уравнения f(x)=0 с использованием средств пакета Matlab, для чего:
-
Постройте графики функции f(x) и ее первой производной;
-
на выбранном отрезке пересечения графика с осью ОХ получить таблицы значений функции f(x) и ее первой производной;
-
проверить условие существования единственного корня на выбранном отрезке;
-
Решите нелинейное уравнение с использованием функций fzero() и solve();
-
Предъявите результаты выполнение задания на ПК преподавателю.
-
Варианты индивидуальных заданий
Таблица 2.1.2-1
|
№ |
Уравнение |
№ |
Уравнение |
|
1 |
|
16 |
|
|
2 |
|
17 |
|
|
3 |
|
18 |
|
|
4 |
|
19 |
|
|
5 |
|
20 |
|
|
6 |
|
21 |
|
|
7 |
|
22 |
|
|
8 |
|
23 |
|
|
9 |
|
24 |
|
|
10 |
|
25 |
|
|
11 |
|
26 |
|
|
12 |
|
27 |
|
|
13 |
|
28 |
|
|
14 |
|
29 |
|
|
15 |
|
30 |
|
-
Содержание отчета
-
В форме комментариев:
-
Название лабораторной работы
-
ФИО студента, номер группы
-
№ варианта
-
Индивидуальное задание
2) Протокол вычислений (сессии) в окне Command Window, снабженный необходимыми комментариями.
2.1.3. Контрольные вопросы по теме
-
Что называется, нелинейным уравнением?
-
Этапы решения нелинейного уравнения.
-
Графическое отделение корней нелинейного уравнения средствами Matlab.
-
Аналитическое отделение корней нелинейного уравнения средствами Matlab.
-
Способы задания функции нелинейного уравнения.
-
Назначение и формат функции fzero().
-
Назначение и формат функции solve().
-
Назначение и формат функции roots().
Тема
2.2. Технология аппроксимации
интерполяции
функций в среде пакета MatLab
2.2.1. Аппроксимация и интерполяция функций
2.2.2. Лабораторная работа по теме «Технология аппроксимации
интерполяции функций в среде пакета MatLab»
2.2.3. Контрольные вопросы по теме
2.2.1. Аппроксимация и интерполяция функций
Пусть имеется набор узловых точек xk (где k=1,2,…,n) и значения функции y(xk) в этих точках, а также некоторая функция f(x,a1, a2, …,am), которая кроме аргумента х зависит еще и от параметров as (где s=1, 2, …m). Задача аппроксимации состоит в том, чтобы подобрать такие значения параметров as, что функция f(x, a1, a2, …am) наилучшим образом описывала бы исходную функцию. Как правило, m<<n, поэтому добиться, чтобы функция f(x, a1, a2, …am) давала точные результаты даже в узловых точках не удастся. Нужен критерий, который оценивает точность аппроксимации таблично заданной функции. Например, в методе наименьших квадратов в качестве такого критерия используется среднеквадратическое отклонение
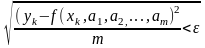 .
.
Частным случаем задачи аппроксимации является задача интерполяции функции. В этом случае также имеем набор узловых точек xk (где k=1,2,…,n) и значения функции yk в этих точках. Однако, в соответствии с критерием интерполяции, требуется построить такую функцию f(x), которая в узловых точках x1, x2,…,xn принимала бы значения y1, y2, …,yn, то есть f(xk) = yk для всех k от 1 до n.Чаще всего функцию f(x) ищут в виде полинома, степень которого n-1. Поэтому задача сводится к определению коэффициентов интерполяционного полинома на основании значений функции в базовых точках.
На практике для решения задачи интерполяции (вычисления значений функции в точках, несовпадающих с узлами интерполяции) используются интерполяционные формулы Ньютона и формула Лагранжа [1].
Для выполнения полиномиальной аппроксимации в MatLab используется функция polyfit(). Эта функция предназначена для выполнения аппроксимации методом наименьших квадратов. Функция polyfit(x,y,n) возвращает вектор коэффициентов полинома степени n, который с наименьшей среднеквадратичной погрешностью аппроксимирует функцию, заданную таблично. Результатом является вектор строка длиной n+1, содержащий коэффициенты полинома в порядке уменьшения степеней. Аргументами функции являются список узловых точек, список значений интерполируемой функции в этих точках и степень интерполяционного полинома. Как правило, степень полинома много меньше количества узлов (m<<n). В качестве результата возвращается список коэффициентов аппроксимирующего полинома.
Ниже приведены пример линейной и кубической аппроксимации функции, заданной таблицей (рис. 2.2.1-1), и графики аппроксимирующих функций (рис. 2.2.1-2).
|
|
Рис. 2.2.1-1. Пример линейной и кубической аппроксимации функции
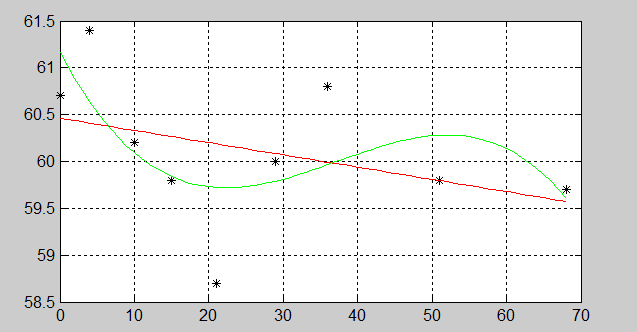
Рис. 2.2.1-2. Графики исходной и аппроксимирующих функций
Чтобы результатом выполнения функции Matlabpolyfit() был именно интерполяционный полином, необходимо, чтобы степень этого полинома была на единицу меньше количества узловых точек.
Пример
2.2.1-1.
Используя
в качестве узлов
интерполяции
x=-5,-4…5,
построить полином, интерполирующий
функцию
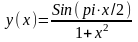 .
.
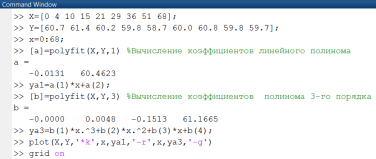
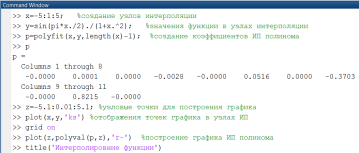
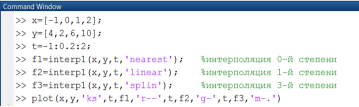
Выполняя команды Matlab в окне Command Window, получим таблицу значений функции и проведем ее интерполяцию с использованием функции Matlab polyfit() (рис. 2.2.1-3). Графики интерполяционных узлов и интерполяционного полинома приведены на рис. 2.2.1-4.Здесь для вычисления значений полинома в точках используется функция polival(p,z), где вектор z покрывает интервал интерполяции и даже выходит за его пределы.
|
|
Рис. 2.2.1-3. Интерполяция таблично заданной функции
с использованием функции Matlab polyfit()
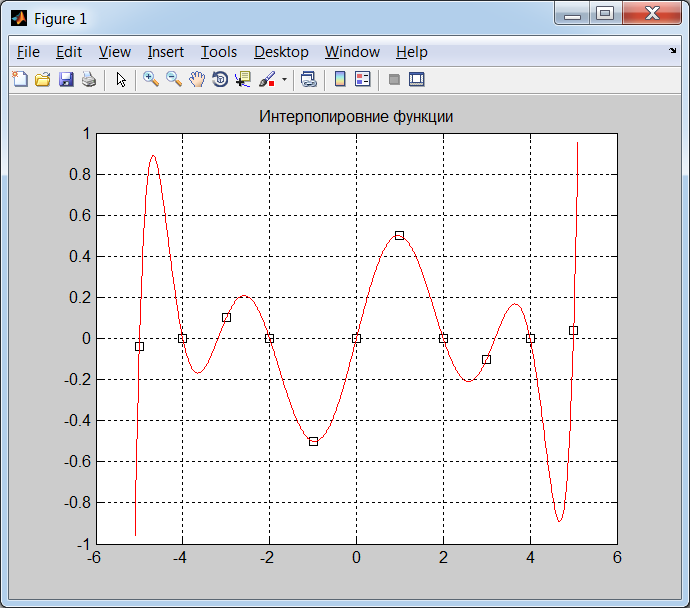
Рис. 2.2.1-4. Графики интерполируемой и интерполирующей функций
При большом количестве базовых точек интерполяция полиномом может оказаться малопродуктивной, поэтому нередко используют интерполяцию сплайнами. Идея сплайн-интерполяции состоит в разбиении диапазона интерполирования на отрезки, в пределах которых используются разные функции одного вида (чаще всего алгебраические многочлены). Эта функция и ее несколько производных на всем диапазоне интерполяции непрерывны. В результате имеем кусочно-гладкую интерполяционную зависимость.
Сплайн-интерполяцию можно реализовать с помощью функции Matlabinterp1(). В качестве аргументов функции передают: набор узловых точек аргумента, значения функции в этих точках, список значений точек, для которых вычисляется значения интерполяционной зависимости и, наконец (в апострофах), тип базового полинома (табл. 2.2.1-1).
Таблица 2.2.1-1
|
Имя функции |
Описание |
|
nearest() |
Интерполяция полиномами нулевой степени – график имеет ступенчатый вид |
|
linear() |
Интерполяция полиномами первой степени – базовые точки соединяются отрезками прямой |
|
spline() |
Интерполяция полиномами третьей степени |
Рассмотрим пример использования функции Matlab interp1().
|
x |
-1 |
0 |
1 |
2 |
|
y(x) |
4 |
2 |
0 |
1 |
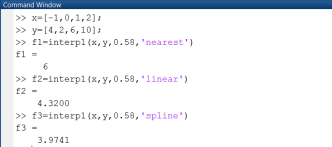
выполнить сплайн-интерполяцию с использованием полиномов нулевой, первой и третьей степени, и получить значения функции в точке х=0.58.
|
|
Рис. 2.2.1-5. Вычисление функции в точке х=0.58
На рис. 2.2.1-6 и 2.2.1-7 приведены команды, необходимые для проведения интерполяции таблично заданной функции и построения графиков интерполируемой функции и интерполирующих ее интерполяционных многочленов различных степеней.
|
|
Рис. 2.2.2-6. Команды построения графиков интерполяционных функций
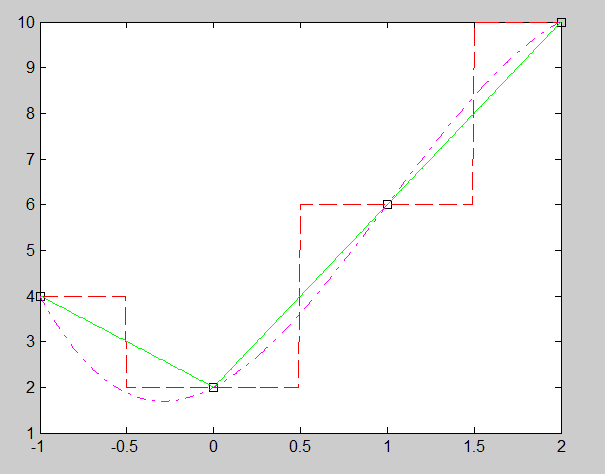
Рис. 2.2.2-7. Графики интерполирующих функций
2.2.2. Лабораторная работа по теме
«Технология аппроксимации интерполяции функций»
-
Вопросы, подлежащие изучению
-
Задание векторов и матриц в пакете Matlab.
-
Технология аппроксимации функции, заданной таблично, с использованием функций polyfit().
-
Технология линейной, кубической и сплайн-интерполяции таблично заданной функции с использованием функций interp1().
-
Получение интерполяционных многочленов в явном виде.
-
Построение графиков аппроксимирующих и интерполирующих функций.
-
Общее задание
-
Изучите материал Темы 2.2. (п. 2.2.1).
-
Выберите индивидуальное задание: номера узлов и номер аппроксимируемой функции из табл. 2.2.2-1; узлы аппроксимации и значения функции в узлах из табл. 2.2.2-2.
-
Задайте в виде векторов значения узлов и значения функции в выбранных узлах.
-
Вычислите коэффициенты аппроксимирующих функций для линейной, квадратичной и кубической аппроксимации с использованием функции polyfit() и получите три аппроксимирующие функции в явном виде.
-
Получите с использованием этих функций значение аппроксимирующей функции в произвольной точке, принадлежащей отрезку, но не совпадающей с узлами аппроксимации, и сравните полученные результаты.
-
Постройте графики табличной и трех аппроксимирующих функций в одном шаблоне, снабдив их легендой.
-
Проведите линейную и кубическую интерполяцию функции с использованием функции interp1(), заданной таблично. Получив значения интерполирующей функции в точке, не совпадающей с узлами интерполяции, сравните полученные результаты.
-
Постройте графики табличной и двух интерполирующих функций в одном шаблоне, снабдив их легендой.
-
Представьте результаты работы преподавателю, ответьте на поставленные вопросы.
-
Выполните команду clear all.
-
Оформите отчет по выполненной работе.
-
Варианты заданий
Таблица 2.2.2-1
Вариант № |
Номера узлов xi |
Номер функции |
|
1 |
1 3 5 7 9 10 13 |
|
|
2 |
1 2 4 5 7 10 12 |
|
|
3 |
1 3 6 7 10 11 13 |
|
|
4 |
1 2 4 7 9 11 13 |
|
|
5 |
3 6 7 9 10 11 12 |
|
|
6 |
2 3 6 8 9 10 13 |
|
|
7 |
1 4 5 7 9 11 12 |
|
|
8 |
1 2 4 7 9 12 13 |
|
|
9 |
2 3 5 7 8 11 12 |
|
|
10 |
1 3 6 7 9 10 13 |
|
|
11 |
1 3 7 8 10 11 13 |
|
|
12 |
1 2 5 6 7 10 12 |
|
|
13 |
1 4 5 8 10 12 13 |
|
|
14 |
1 3 5 7 9 10 13 |
|
|
15 |
1 3 6 7 8 10 13 |
|
|
16 |
1 4 5 7 9 11 12 |
|
|
17 |
2 4 5 6 8 12 13 |
|
|
18 |
1 4 5 7 9 11 12 |
|
|
19 |
1 4 5 8 10 11 12 |
|
|
20 |
2 4 5 6 8 12 13 |
|
|
21 |
1 4 5 8 10 12 13 |
|
|
22 |
2 3 6 8 9 10 13 |
|
|
23 |
1 3 5 8 10 12 13 |
|
|
24 |
1 4 5 7 9 11 12 |
|
|
25 |
2 4 5 6 8 12 13 |
|
|
26 |
3 4 5 7 8 9 12 |
|
|
27 |
3 5 8 10 11 12 13 |
|
|
28 |
2 4 7 9 10 11 13 |
|
|
29 |
2 4 5 7 8 10 12 |
|
|
30 |
1 4 5 7 9 11 13 |
|
Таблица 2.2.2-2
i |
xi |
|
|
|
|
1 |
-5 |
1.38 |
2.44 |
1.676 |
|
2 |
-4.5 |
1.221 |
2.359 |
2.025 |
|
3 |
-4 |
1.511 |
1.751 |
1.736 |
|
4 |
-3.5 |
1.501 |
2.13 |
1.203 |
|
5 |
-3 |
1 |
1.455 |
1.511 |
|
6 |
-2.5 |
0.728 |
1.482 |
1.362 |
|
7 |
-2 |
0.976 |
1.437 |
0.75 |
|
8 |
-1.5 |
1.065 |
0.803 |
0.976 |
|
9 |
-1 |
0.599 |
1.175 |
0.957 |
|
10 |
-0.5 |
0.192 |
0.49 |
0.272 |
|
11 |
0 |
0.3 |
0.375 |
0.3 |
|
12 |
0.5 |
0.319 |
-6.51*10-3 |
0.165 |
|
13 |
1 |
-0.405 |
-1.965 |
-1.185 |
-
Содержание отчета
-
В форме комментариев:
-
Название лабораторной работы
-
ФИО студента, номер группы
-
№ варианта
-
Индивидуальное задание
-
Протокол вычислений (сессии) в окне Command Window, снабженный необходимыми комментариями.
2.2.3. Контрольные вопросы по теме
-
Что такое аппроксимация функции и в каких случаях она используется?
-
В чем отличие аппроксимации от интерполяции?
-
Какой метод аппроксимации реализован в функции polyfit()?
-
Что служит результатом выполнения функции polyfit()?
-
Для чего предназначена функция polyval()?
-
Назначение и формат функции interp1()?
-
Каким параметром определяется тип интерполяции в функции interp1()?
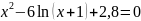
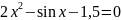
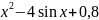 =0
=0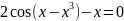
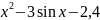
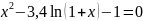
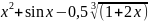 =0
=0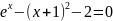
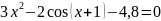
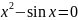
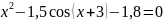
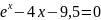

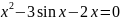
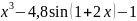 =0
=0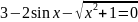
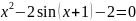
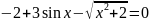
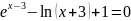
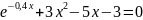
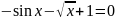
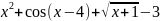 =0
=0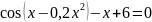
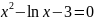
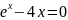
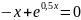
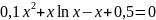
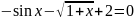
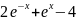 =0
=0