ВУЗ: Пермский национальный исследовательский политехнический университет
Категория: Лекция
Дисциплина: Программирование
Добавлен: 19.10.2018
Просмотров: 5031
Скачиваний: 11
СОДЕРЖАНИЕ
1.2.Описание стандартных типов данных
Вычисление выражений с использованием стандартных функций
Вычисление выражений с использованием стандартных функций.
Описание используемых стандартных функций.
2.1. Составной и пустой операторы.
Решение уравнений и неравенств с использованием условного оператора.
Лабораторная работа № 2, вариант № 8.
Решение уравнений и неравенств с использованием условного оператора.
Лабораторная работа № 3, вариант № 8.
Организация циклов в программе.
Лабораторная работа № 4, вариант № 8.
Организация циклов в программе.
3.3. Метод половинного деления.
Лабораторная работа № 5, вариант № 3.
Решение нелинейных уравнений методом итераций.
Распечатка результатов работы программы в следующем виде:
Лабораторная работа № 5, вариант № 3.
Решение нелинейных уравнений методом Ньютона.
Распечатка результатов работы программы в следующем виде:
Лабораторная работа № 5, вариант № 3.
Решение нелинейных уравнений методом половинного деления.
Описание метода половинного деления:
Блок-схема метода половинного деления:
Распечатка результатов работы программы в следующем виде:
Метод Монте-Карло (метод статистических испытаний)
5.2.2. Классы задач по обработке массивов.
5.2.2.1. Однотипная обработка всех или указанных элементов массивов.
5.2.2.2. Задачи, в результате решения которых изменяется структура массива.
5.2.2.3. Обработка нескольких массивов одновременно.
5.2.2.4. Поисковые задачи для массивов.
5.2.2.5.1. Сортировка вставкой
5.2.2.5.3. Сортировка обменом («пузырьковая сортировка»)
5.2.2.5.4. Сортировка фон Неймана (слиянием)
5.3.1. Описание двумерных массивов.
5.3.2. Сортировка двумерных массивов
6.2. Процедуры обработки строк.
Лабораторная работа № 7, вариант № 8.
7. Комбинированные типы. Оператор присоединения
Работа с комбинированными типами данных.
Лабораторная работа № 8, вариант № 8.
Работа с комбинированными типами данных.
Работа с множественными типами данных.
Лабораторная работа № 9, вариант № 3.




L = J




J = J + 1
I = I + 1




Программа реализующая метод выбора, будет иметь следующий вид:
Program Selection Sort;
Uses Crt;
const
n=20; { длина массива}
typc
TVector = array 1…n of Real;
Var
Vector : TVector;
Min : Real;
Imin, S: Integer;
i : Integer;
Begin
Clr Srt:
Writeln (‘введите элементы массива:’);
for i: = 1 to n do Read (Vector i); Readln;
{ - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - }
for S:=1 to n-1 do
begin
{поиск минимального элемента в диапазоне от }
{S-го элемента до n-го}
Min: = Vector S;
I min: = S;
For i: = S+1 to n do
If Vector i Min then
begin
Min: = Vector i;
I min: = I;
End;
{обмен местами минимального и S-го элемента}
Vector Imin: = Vector S;
Vector S: = Min;
End;
{ - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - }
Writeln (‘Отсортированный массив:’);
For i: = 1 to n do Write (Vector i: 8 : 2);
Writeln;
End.
Результат работы :
|
Bведите элементы массива : 7654098321 Отсортированный массив : 0123456789 |
5.2.2.5.3. Сортировка обменом («пузырьковая сортировка»)
Слева направо поочередно сравниваются два соседних элемента, и если их взаиморасположение не соответствует заданному условию упорядоченности, то они меняются. Далее берутся два следующих соседних элемента и так далее до конца массива. После одного такого прохода на последний n-ой позиции массива будет стоять максимальный элемент («всплыл первый пузырек»). Поскольку максимальный элемент уже стоит на своей последней позиции, то второй проход обменов выполняется до n-1 элемента. И так далее. Всего требуется n-1 проход.
1 шаг:
шаг:
-
5
11
3
7
1
4
2
9



 3 11
3 11

 7 11
2 11 9 11
7 11
2 11 9 11
2 шаг: 1 11 4 11
шаг: 1 11 4 11
-

 5
53
7
1
4
2
9
11
 3 5 1 7
3 5 1 7

 4
7
4
7
3 шаг: 2 7
-
3
5
1
4
2
7
9
11

 1 5
1 5
 4 5
4 5
4 шаг: 2 5
шаг: 2 5
-
3
1
4
2
5
7
9
11

 1 3 2 4
1 3 2 4
5 шаг:
шаг:
-
 1
13
2
4
5
7
9
11
2 3
6 шаг:
шаг:
-
1
2
3
4
5
7
9
11
7 шаг:
шаг:
-
1
2
3
4
5
7
9
11
Р езультат:
езультат:
-
1
2
3
4
5
7
9
11
Б ЛОК
– СХЕМА
ЛОК
– СХЕМА
I = 2



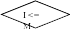 1
1




K = M



 1
1




I = I + 1

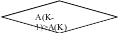




 1
1
R = A(K-1) A(K-1)=A(K) A(K) = R



K = K-1


Программа реализирующая метод обмена («пузырька»), будет иметь следующий вид:
Program Duddle Sort;
Uses Crt;
Const
N = 20; { длина массива}
Type
TVector = array 1…n of Real;
Var
Vector : Tvector;
B : Real;
i, K : Integer;
begin
ClrScr;
Writeln (‘введите элементы массива:’);
for i: = 1 to n do Read (Vector [i]); Readln;
{- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - }
for K: = n downto 2 do
{“всплывание” очередного максимального элемента}
{на К-ю позицию}
for i: = 1 to K-1 do
if Vector [i] > Vector [i+1] then
begin
B: = Vector [i];
Vector [i]: = Vector [i+1];
Vector [i+1]: = B;
End;
{- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - }
Writeln (‘отсортированный массив:’);
For i: = 1 to n do Write (‘Vector [i]: 8 : 2’);
Writeln;
End.
Результат работы:
|
Bведите элементы массива: 7654098321 Отсортированный массив: 0123456789
|
5.2.2.5.4. Сортировка фон Неймана (слиянием)
Заданы два упорядоченных по возрастанию элементов одномерных массива: а размерности n и b размерности m. Требуется получить третий массив с размерности n+m, который содержал бы все элементы исходных массивов, упорядоченных по возрастанию.
Алгоритм решения этой задачи известен как «сортировка фон Неймана» или сортировка слиянием. Идея алгоритма состоит в следующем. Сначала анализируются первые элементы обоих массивов. Меньший элемент переписывается в новый массив. Оставшийся элемент последовательно сравнивается с элементами из другого массива. В новый массив после каждого сравнения попадает меньший элемент. Процесс продолжается до исчерпания элементов одного из массивов. Затем остаток другого массива дописывается в новый массив. Полученный новый массив упорядочен таким же образом, как исходные.
Программа, реализующая метод Фон-Неймана, имеет следующий вид:
БЛОК – СХЕМА
I = 1 J = 1 K = 1



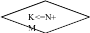 1
1




 1
1





 1
1




 1
1




[(K)=B(J)] J = J+1 K = K+1 [(K)=A(I)] I = I+1 K = K+1 K=N+M+1







[(K)=B(J)] J = J+1 K = K+1

[(K)=A(I)] I = I+1 K = K+1










program confluence;
const n = 10;
m = 20;
l = n + m;
var x: array [1..n] of integer;
y: array [1..m] of integer;
z: array [1..l] of integer;
k, i, j: integer;
begin
for i: = 1 to n do
read (x[i]); {формирование первого упорядоченного массива}
for i: = 1 to m do
read (y[i]); {формирование второго упорядоченного массива}
I:= 1; j:=1; l:=1 {i-индекс первого массива, j-индекс второго
массива, l-индекс результирующего массива}
while (i<=n) and (j<=m) do {пока не закончились элементы в одном из массивов}
if x[i] < y[i] then {переписываем элементы из первого массива}
begin
z[k]: = x[i];
i: = i + 1; k: = k + 1;
end
else {переписываем элемент из второго массива}
begin
z[k]: = y[j];
j: = j + 1; k: = k + 1;
end;
while i < = n do {если не закончились элементы в первом массиве,}
begin {переписываем их в результирующий массив}
z[k]: = x[i]; i: = i + 1; k: = k+1;
end;
while j < = m do {если не закончились элементы во втором массиве}
begin {переписываем их в результирующий массив}
z[k]: = y[j]; j: = j + 1; k: = k+ 1;
end;
for i: = 1 to l do {вывод на экран упорядоченного массива,}
writeln (z[i]); {полученного слиянием}
End.
Результаты работы:
|
0123456789 0123456789 00112233445566778899
|
5.2.2.5.5. Шейкер-сортировка
Шейкер — сортировка является модификацией сортировки методом пузырька. Здесь, как и в методе пузырька проводят попарное сравнение элементов и обменов в паре. Если имеется необходимость, но первый проход осуществляют снизу вверх, второй – сверху вниз и т.д. Иными словами меняется направление прохода.
program sheyker;
uses crt;
const n=30;
var a:array[1..n]of integer;
x,j,i,u:integer;
h:boolean;
begin
clrscr;
writeln('Массив до сортировки:');
for i:=1 to n do
begin
a[i]:=round(random*999);
write(a[i],'-');
end;
writeln;
writeln('Массив после сортировки:');
h:=true;u:=n;i:=2;
repeat
if h then begin
for j:=u downto i do
if a[j-1]>a[j] then begin
x:=a[j-1];
a[j-1]:=a[j];
a[j]:=x;
h:=false;
end;
u:=u-1;
end
else begin
for j:=i to u do
if a[j+1]<a[j] then begin
x:=a[j+1];
a[j+1]:=a[j];
a[j]:=x;
h:=true;
end;
i:=i+1;
end;
until u=i;
for i:=1 to n do
write(a[i],'-');
readln;
end.
Результаты выполнения программы:
|
Массив до сортировки: 0-31-860-202-273-671-318-162-372-425-82-474-70-840-60-293-916-368-774-328-697-84 3-717-306-162-329-466-246-825-279- Массив после сортировки: 0-31-60-70-82-162-162-202-246-273-279-293-306-318-328-329-368-372-425-466-474-67 1-697-717-774-825-840-843-860-916- |
5.3. Двумерные массивы.
5.3.1. Описание двумерных массивов.
Двумерный массив можно рассматривать как одномерный массив, каждый элемент которого сам является одномерным массивом. Поэтому для работы с элементами двумерного массива нужно организовать два цикла. Каждый из них отвечает за перебор значений соответствующего индекса. Для двумерного массива можно использовать те же схемы перебора, что и для одномерного, но комбинаций здесь будет в два раза больше.
Рассмотрим один из способов ввода элементов двумерного массива. Будем использовать схему перебора по одному от начала массива к концу. Считаем что массив имеет размерность n * m
For i : = 1 to n do {перебираем строки двумерного массива}
For j: = 1 to m do {перебираем столбцы двумерного массива}
Read (a [i,j]).
Транспонирование двумерного массива, значит переставить местами его стоки и столбцы. Например для исходного массива:
2 3 получить: 1 4 7
4 5 6 2 5 8
7 8 9 3 6 9
Из приведенного примера хорошо видно, что диагональные элементы в результате обмена остаются на своих местах, обмениваются местами элементы, расположенные симметрично относительно главной диагонали.
For i: = 1 to n do{перебираем все строки массива}
For j: = 1 to i-1 do {перебираем элементы до главной диагонали}
Begin r: = a [i, j]; a [i, j]: = a [j, i]; a [j,i]: = r ; end.
Нахождение максимального (минимального) элемента двумерного массива. Эта задача совпадает с решением задачи для одномерного массива. Отличие заключается в необходимости для двумерного массива вложенных циклов перебора. Фрагмент программы приведен ниже:
i max: =1; j max: = 1;{предлагаем максимальный первый элемент}
for i: = 1 to n do
for j: = 1 to n do
if a [i max, j max] < a [i, j]
then begin i max: = i; jmax = j; end.
5.3.2. Сортировка двумерных массивов
Отсортировать элементы двумерного массива по элементам второй строки.
Исходный массив. Результат
1 2 3 4 5 5 2 4 3 1
9 3 7 3 1 1 3 3 7 9
6 7 8 9 1 1 7 9 8 6
От сортировки одномерного массива этот случай отличается только тем, что переставлять нужно не два сравниваемых элемента, а два столбца:
for i: = 1 to n – 1 do
for j: = i+1 to n do
if a [2, i] > a [2, j]
then for k: = 1 to n do
begin r: = a [k, i]; a [k, i]; = a[k, j]; a [k, j]: =r
end.
{Сортировка массивов}
{ 1. Вставками }
{ 2. Обменом }
{ 3. Выбором }
{ 4. Фон Неймана (Слияние двух отсортированных массивов)}
program sor1;
uses crt;
const n=4;
var mas:array[1..n,1..n]of integer;
buf,l,i,j,a,c,nextmas:integer;
quit:boolean;
procedure print;
begin
for i:=1 to n do
begin
for j:=1 to n do
write(' ',mas[i,j],' ');
writeln;
end;
writeln;writeln('Ќ ¦¬ЁвҐ Enter ¤«п Їа®¤®«¦ҐЁп !');
readln;
end;
procedure next;
begin
j:=j+1;
if j=n+1 then begin j:=1;i:=i+1;end;
end;
procedure last;
begin
j:=j-1;
if j=0 then begin j:=n;i:=i-1;end;
end;
begin
clrscr;
for i:=1 to n do
for j:=1 to n do
mas[i,j]:=round(random*(9));
print;
i:=1;j:=1;
for l:=2 to (n*n) do
begin
next;buf:=mas[i,j];a:=i;c:=j;
last;quit:=true;
while (buf<mas[i,j])and(quit) do
begin
nextmas:=mas[i,j];
mas[i,j]:=buf;
next;mas[i,j]:=nextmas;last;last;
if j=0 then quit:=false;
end;
i:=a;j:=c;
end;
print;
end.
Результаты работы:
|
0 0 8 2 2 6 3 1 3 4 1 4 1 8 1 3 Нажмите Enter для продолжения ! 0 0 1 1 1 1 2 2 3 3 3 4 4 6 8 8 Нажмите Enter для продолжения !
|
program sor2;
uses crt;
const n=4;
var mas:array[1..n,1..n]of integer;
buf,l,units,i,j,nextmas:integer;
quit:boolean;
procedure print;
begin
for i:=1 to n do
begin
for j:=1 to n do
write(' ',mas[i,j],' ');
writeln;
end;
writeln;writeln('Ќ ¦¬ЁвҐ Enter ¤«п Їа®¤®«¦ҐЁп !');
readln;
end;
procedure next;
begin
j:=j+1;
if j=n+1 then begin j:=1;i:=i+1;end;
end;
procedure last;
begin
j:=j-1;
if j=0 then begin j:=n;i:=i-1;end;
end;
begin
clrscr;
units:=n*n;
for i:=1 to n do
for j:=1 to n do
mas[i,j]:=round(random*9);
print;
repeat
i:=1;j:=1;
quit:=true;
units:=units-1;
for l:=1 to units do
begin
next;nextmas:=mas[i,j];last;
if mas[i,j]>nextmas
then begin buf:=mas[i,j];mas[i,j]:=nextmas;next;mas[i,j]:=buf;quit:=false;end
else next;
end;
until quit or (units=1);
print;
end.
Результаты работы:
|
0 0 8 2 2 6 3 1 3 4 1 4 1 8 1 3 Нажмите Enter для продолжения ! 0 0 1 1 1 1 2 2 3 3 3 4 4 6 8 8 Нажмите Enter для продолжения !
|
program sor3;

