ВУЗ: Пермский национальный исследовательский политехнический университет
Категория: Лекция
Дисциплина: Программирование
Добавлен: 19.10.2018
Просмотров: 5068
Скачиваний: 11
СОДЕРЖАНИЕ
1.2.Описание стандартных типов данных
Вычисление выражений с использованием стандартных функций
Вычисление выражений с использованием стандартных функций.
Описание используемых стандартных функций.
2.1. Составной и пустой операторы.
Решение уравнений и неравенств с использованием условного оператора.
Лабораторная работа № 2, вариант № 8.
Решение уравнений и неравенств с использованием условного оператора.
Лабораторная работа № 3, вариант № 8.
Организация циклов в программе.
Лабораторная работа № 4, вариант № 8.
Организация циклов в программе.
3.3. Метод половинного деления.
Лабораторная работа № 5, вариант № 3.
Решение нелинейных уравнений методом итераций.
Распечатка результатов работы программы в следующем виде:
Лабораторная работа № 5, вариант № 3.
Решение нелинейных уравнений методом Ньютона.
Распечатка результатов работы программы в следующем виде:
Лабораторная работа № 5, вариант № 3.
Решение нелинейных уравнений методом половинного деления.
Описание метода половинного деления:
Блок-схема метода половинного деления:
Распечатка результатов работы программы в следующем виде:
Метод Монте-Карло (метод статистических испытаний)
5.2.2. Классы задач по обработке массивов.
5.2.2.1. Однотипная обработка всех или указанных элементов массивов.
5.2.2.2. Задачи, в результате решения которых изменяется структура массива.
5.2.2.3. Обработка нескольких массивов одновременно.
5.2.2.4. Поисковые задачи для массивов.
5.2.2.5.1. Сортировка вставкой
5.2.2.5.3. Сортировка обменом («пузырьковая сортировка»)
5.2.2.5.4. Сортировка фон Неймана (слиянием)
5.3.1. Описание двумерных массивов.
5.3.2. Сортировка двумерных массивов
6.2. Процедуры обработки строк.
Лабораторная работа № 7, вариант № 8.
7. Комбинированные типы. Оператор присоединения
Работа с комбинированными типами данных.
Лабораторная работа № 8, вариант № 8.
Работа с комбинированными типами данных.
Работа с множественными типами данных.
Лабораторная работа № 9, вариант № 3.
Постановка задачи:
-
Для конкретного варианта найти корень уравнения F(x) = 0 с точностью =10-4, используя один из численных методов. На печать вывести вычисленное значение корня и для сравнения точное значение корня.
-
Значения a, b, x0, вводятся с клавиатуры. Должен быть предусмотрен контроль вводимых значений.
-
В программе необходимо предусмотреть подсчет и вывод на печать числа итераций, за которое удается найти значение корня с заданной точностью.
Содержание отчета :
-
Постановка задачи для конкретного варианта и исходные данные.
-
Описание и блок-схема метода решения.
-
Текст программы.
Распечатка результатов работы программы в следующем виде:
РЕШЕНИЕ УРАВНЕНИЯ
ТОЧНОЕ ЗНАЧЕНИЕ КОРНЯ .............................
ВЫЧИСЛЕННОЕ ЗНАЧЕНИЕ КОРНЯ .............….
ЧИСЛО ИТЕРАЦИЙ ...........................................
Образец выполнения задания.
Лабораторная работа № 5, вариант № 3.
Решение нелинейных уравнений методом итераций.
Постановка задачи для конкретного варианта и исходные данные:
1. Найти корень уравнения
:
![]() с точностью =10-4,
корень уравнения находится на отрезке
(0.4, 1), используя метод итераций. На печать
вывести вычисленное значение корня и
для сравнения точное значение корня,
точное значение корня x=0.7376.
с точностью =10-4,
корень уравнения находится на отрезке
(0.4, 1), используя метод итераций. На печать
вывести вычисленное значение корня и
для сравнения точное значение корня,
точное значение корня x=0.7376.
Значения :
Xо – примерное значение корня,
- точность нахождения корня, вводятся с клавиатуры.
Должен быть предусмотрен контроль вводимых значений.
2. В программе необходимо предусмотреть подсчет и вывод на печать числа итераций, за которое удается найти значение корня с заданной точностью.
Описание и блок-схема метода решения:
Описание метода итераций:
Пусть уравнение
![]() имеет один корень на отрезке [a;b]. Функция
F(x) непрерывна на отрезке [a; b].
имеет один корень на отрезке [a;b]. Функция
F(x) непрерывна на отрезке [a; b].
Этот метод заключается
в замене уравнения
![]() эквивалентным ему уравнением вида
эквивалентным ему уравнением вида
![]()
![]()
После этого строится итерационный процесс:
На заданном отрезке [a; b] выберем точку х0 – нулевое приближение – и найдем:
х1 = f(x0),
потом найдем:
х2 = f(x1),
и т.д.
Таким образом, процесс нахождения корня уравнения сводится к последовательному вычислению чисел:
хn = f(xn-1) n = 1,2,3..... .
Процесс
итераций продолжается до тех пор, пока
![]()
где – заданная абсолютная погрешность корня х.
Блок-схема метода итераций:



![]()

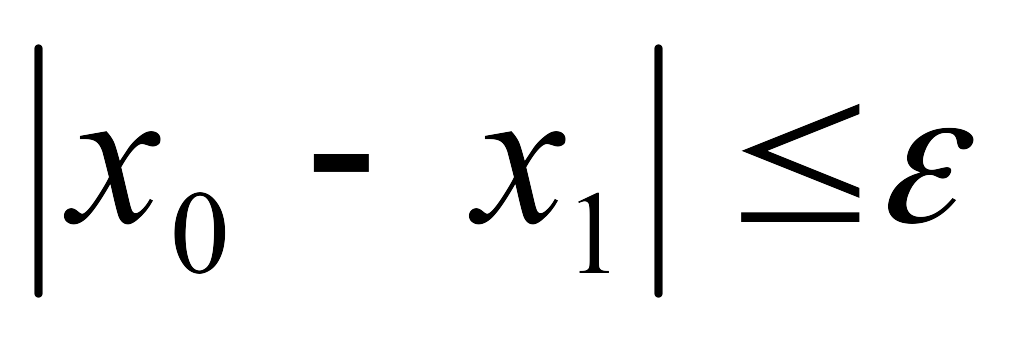 true
false
true
false




![]()




Текст программы.
program lab5{ вариант № 3};
uses crt;
var x0,x1,a,b,e:real;
iteraz:integer;
function fun(x:real):real;
begin
fun:=2.5-sqrt(x)-exp((1/3)*(ln(x)));
end;
begin
clrscr;
write('Введите приближённое значение X=');
readln(x1);
write('Введите точность e=');
readln(e);
iteraz:=0;
repeat
iteraz:=iteraz+1;
x0:=x1;
x1:=fun(x0);
until (abs(x1-x0)<=e);
writeln('Решение уравнения:');
writeln('Точное значение корня...... ……0.7376');
writeln('Вычисленное значение корня…',x1:6:5);
writeln('Число итераций..…………......... ',iteraz);
writeln('Программа закончена, нажмите Enter.');
readln;
end.
Распечатка результатов работы программы в следующем виде:
|
Решение уравнения: Точное значение корня...... ……...0.7376 Вычисленное значение корня.. …0.73767 Число итераций...........………….. ..989 |
Лабораторная работа № 5, вариант № 3.
Решение нелинейных уравнений методом Ньютона.
Постановка задачи для конкретного варианта и исходные данные:
1. Найти корень уравнения
:
![]() с точностью =10-4,
корень уравнения находится на отрезке
(0.4, 1), используя метод Ньютона. На печать
вывести вычисленное значение корня и
для сравнения точное значение корня,
точное значение корня x=0.7376.
с точностью =10-4,
корень уравнения находится на отрезке
(0.4, 1), используя метод Ньютона. На печать
вывести вычисленное значение корня и
для сравнения точное значение корня,
точное значение корня x=0.7376.
Значения :
Xо – примерное значение корня,
- точность нахождения корня, вводятся с клавиатуры.
Должен быть предусмотрен контроль вводимых значений.
2. В программе необходимо предусмотреть подсчет и вывод на печать числа итераций, за которое удается найти значение корня с заданной точностью.
Описание и блок-схема метода решения:
Описание метода Ньютона:
Пусть уравнение
![]() имеет один корень на отрезке [a;b]. Функция
F(x) непрерывна на отрезке [a; b].
имеет один корень на отрезке [a;b]. Функция
F(x) непрерывна на отрезке [a; b].
![]()
![]()
Приводящее к итерационному процессу следующего вида:
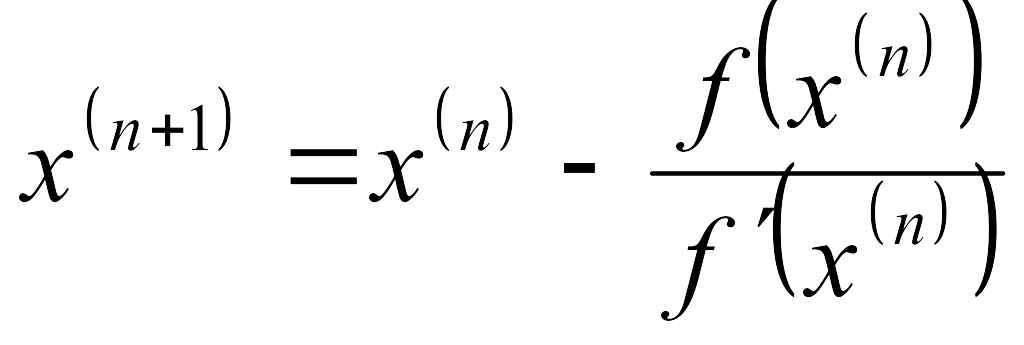
Выберем на отрезке[a; b] произвольную точку х0 – нулевое приближение. Затем найдем:
x1
= x0
-
![]() ,
,
потом x2
= x1
-
![]() .
.
Таким образом, процесс нахождения корня уравнения сводится к вычислению чисел xn по формуле:
xn
= xn-1
-
![]() n = 1,2,3...... .
n = 1,2,3...... .
Процесс вычисления продолжается до тех пор, пока не будет выполнено условие:
![]()
Блок-схема метода Ньютона:


![]()

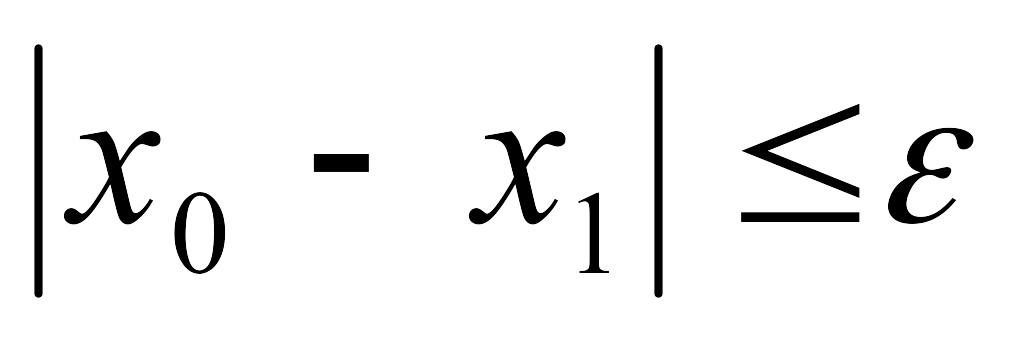 true
false
true
false




![]()




Текст программы.
program lab5{ вариант № 3};
uses crt;
var x0,x1,a,b,e:real;
iteraz:integer;
function fun(x:real):real;
begin
fun:=(x+sqrt(x)+exp((1/3)*(ln(x)))-2.5)/(1+1/(2*sqrt(x))+1/(3*exp((1/3)*(ln(x)))));
end;
begin
clrscr;
write('Введите приближённое значение корня X=');
readln(x1);
write('Введите точность e=');
readln(e);
iteraz:=0;
repeat
iteraz:=iteraz+1;
x0:=x1;
x1:=x0-fun(x0);
until (abs(x1-x0)<=e);
writeln('Решение уравнения:');
writeln('Точное значение корня...... ……0.7376');
writeln('Вычисленное значение корня…',x1:6:5);
writeln('Число итераций..…………......... ',iteraz);
writeln('Программа закончена, нажмите Enter.');
readln;
end.
Распечатка результатов работы программы в следующем виде:
|
Решение уравнения: Точное значение корня...... ……...0.7376 Вычисленное значение корня.. …0.73762 Число итераций...........………… ..3 |
Лабораторная работа № 5, вариант № 3.
Решение нелинейных уравнений методом половинного деления.
Постановка задачи для конкретного варианта и исходные данные:
1. Найти корень уравнения
:
![]() с точностью =10-4,
корень уравнения находится на отрезке
(0.4, 1), используя методов половинного
деления. На печать вывести вычисленное
значение корня и для сравнения точное
значение корня, точное значение корня
x=0.7376.
с точностью =10-4,
корень уравнения находится на отрезке
(0.4, 1), используя методов половинного
деления. На печать вывести вычисленное
значение корня и для сравнения точное
значение корня, точное значение корня
x=0.7376.
Значения :
(a, b) – отрезок на котором находится корень уравнения,
Xо – примерное значение корня,
- точность нахождения корня,
вводятся с клавиатуры.
Должен быть предусмотрен контроль вводимых значений.
2. В программе необходимо предусмотреть подсчет и вывод на печать числа итераций, за которое удается найти значение корня с заданной точностью.
Описание и блок-схема метода решения:
Описание метода половинного деления:
Пусть уравнение
![]() имеет один корень на отрезке [a;b]. Функция
F(x) непрерывна на отрезке [a; b].
имеет один корень на отрезке [a;b]. Функция
F(x) непрерывна на отрезке [a; b].
Метод половинного деления заключается в следующем:
Сначала выбираем
начальное приближение, деля отрезок
пополам, т.е. х0
= (a+b)/2. Если
F(x)=0, то x0
является корнем уравнения. Если F(x)![]() 0, то выбираем тот из отрезков, на концах
которого функция имеет противоположные
знаки. Полученный отрезок снова делим
пополам и выполняем действия сначала
и т.д.
0, то выбираем тот из отрезков, на концах
которого функция имеет противоположные
знаки. Полученный отрезок снова делим
пополам и выполняем действия сначала
и т.д.
Процесс деления отрезка продолжаем до тех пор, пока длина отрезка, на концах которого функция имеет противоположные знаки, не будет меньше заданного числа .
Блок-схема метода половинного деления:





true false




![]()

 false
true
false
true

![]()
![]()


![]()




Текст программы.
program lab5{ вариант № 3};
uses crt;
var x,a,b,e:real;
iteraz:integer;
function fun(x:real):real;
begin
fun:=x+sqrt(x)+exp((1/3)*(ln(x)))-2.5;
end;
begin
repeat
clrscr;
writeln('Корень уравнения находиться на интервале [a,b]');
write('Введите [a=');
readln(a);
write('Введите [b=');
readln(b);
write('Введите приближённое значение корня X=');
readln(x);
write('Введите точность e=');
readln(e);
until (b-a>e) or (x>a) or (x<b) or (a<>0);
iteraz:=0;
while (fun(x)<>0) and (abs(a-b)>e) do
begin
iteraz:=iteraz+1;
if (fun(a)*fun(x))<0
then b:=x
else a:=x;
x:=((a+b)/2);
end;
writeln('Решение уравнения:');
writeln('Точное значение корня....……..0.7376’);
writeln('Вычисленное значение корня.. ',x:6:5);
writeln('Число итераций..........…………. ',iteraz);
writeln('Программа закончена, нажмите Enter.');
readln;
end.
Распечатка результатов работы программы в следующем виде:
|
Решение уравнения: Точное значение корня...... ……..0.73760 Вычисленное значение корня.. …0.73764 Число итераций...........………… ..14 |
Варианты заданий.
|
N0 вар. |
Уравнение |
Отрезок, содержащий корень |
Метод |
Точное значение корня |
|
1 |
|
[2;3] |
Итераций |
2,2985 |
|
2 |
|
[0;2] |
Ньютона |
1,0001 |
|
3 |
|
[0;0,85] |
Итераций |
0,2624 |
|
4 |
|
[1;2] |
Ньютона |
1,1183 |
|
5 |
|
[0;8] |
Половинного деления |
0,3333 |
|
6 |
|
[0;1] |
Итераций |
0,5629 |
|
7 |
|
[2;4] |
Ньютона |
3,2300 |
|
8 |
|
[1;2] |
Половинного деления |
1,8756 |
|
9 |
|
[0;1] |
Итераций |
0,7672 |
|
10 |
ex - e-x -2 = 0 |
[0;1] |
Ньютона |
0,8814 |
|
11 |
|
[1;3] |
Половинного деления |
1,3749 |
|
12 |
|
[1,2;2] |
Итераций |
1,3077 |
|
13 |
|
[3;4] |
Ньютона |
3,5265 |
|
14 |
|
[1;2] |
Половинного деления |
1,0804 |
|
15 |
|
[0;1,5] |
Итераций |
1,1474 |
|
16 |
|
[1;3] |
Ньютона |
2,0692 |
|
17 |
|
[0;1] |
Половинного деления |
0,5768 |
|
18 |
|
[0,5;1] |
Итераций |
0,9892 |
|
19 |
|
[1;3] |
Ньютона |
1,8832 |
|
20 |
|
[0;1] |
Половинного деления |
0,1010 |
|
21 |
|
[2;3] |
Итераций |
2,0267 |
|
22 |
|
[0,4;1] |
Ньютона |
0,6533 |
|
23 |
|
[-1;0] |
Половинного деления |
-0,2877 |
|
24 |
ln x -x + 1,8 = 0 |
[2;3] |
Итераций |
2,8459 |
Мы не можем заранее сказать, какая сторона монеты или игрального кубика окажется сверху, какую карту мы вытащим из колоды. Говорят, что результат такого эксперимента является случайным числом. Повторяя эксперимент много раз, можно получить последовательность случайных чисел. Интересно, что невозможно предвидеть значение нового члена ряда – он не зависит от предыдущих членов.
Случайные числа широко используются в задачах, моделирующих жизненные ситуации (игры, эпидемии заболеваний и др.). В Паскале реализован датчик или генератор псевдослучайных чисел. Числа, вырабатываемые при помощи приведенных ниже функций, называют псевдослучайными («похожими» на случайные), поскольку это модель случайных чисел, иногда весьма приближенная.
Randomize – инициирует датчик.
Random – генерирует случайные действительные числа из диапазона [0;1]
Random (x) – генерирует любые случайные целые числа из диапазона [0;x].
Random (x) + random – генерирует случайное действительное число из диапазона [0;x];
Random (x) + random + y – генерирует случайное действительное число из диапазона [y; x + y];
Random (x) + random – y – генерирует случайное действительное число из диапазона [-y; x – y];
2* x* Random – x – генерирует случайное действительное число из диапазона [-x; x].
Метод Монте-Карло (метод статистических испытаний)
Случайные числа широко используются для приближенного вычисления площади с помощью метода Монте-Карло. Суть метода очень проста. Пусть есть некоторая фигура, площадь которой необходимо вычислить. Размещаем эту фигуру внутри стандартного квадрата со сторонами, параллельными осям. Пусть про любую точку квадрата можно узнать попадает ли эта точка внутрь фигуры или нет. Тогда площадь может быть вычислена следующим образом: поделив количество точек, попавших внутрь фигуры, на количество всех точек, попавших в квадрат, можно узнать, какую часть площади квадрата занимает фигура, домножив это отношение на площадь квадрата, получим площадь фигуры. Ясно, что число точек, попавших внутрь фигуры тем больше, чем больше фигура, а точность решения будет пропорциональна количеству точек в квадрате. Пара случайных чисел в этом методе может быть рассмотрена как координаты точки на плоскости.
Пример: Определить площадь круга с радиусом R=1.
Решение:
program task;
var i,n, m: integer; {n- общее кол-во точек, m- кол-во точек внутри круга}
x, y: real; {координаты точки}
begin
wriiteln (‘задайте количество точек’);
readin (n);
Randomize;
m: = 0;
for i: = 1 to n do
begin
x: = 2* random – 1; y: = 2* random – 1;
if sqr (x) + sqr (y) < = 1 then m: - m + 1;
end;
writeln ('площадь круга равна ‘, 4* m/n);
readln;
End.
Результаты выполнения программы:
|
Задайте количество точек: 8 Площадь круга равна : 2.5000000000E+00 |
5. Массивы.
5.1. Процедуры и функции.
Процедуры и функции представляют собой важный инструмент ТР, позволяющий писать хорошо структурированные программы.
Процедура представляет собой отдельную часть программы, которая имеет своё имя.
Процедуры и функции представляют собой относительно самостоятельные фрагменты программы, оформленные определенным образом и снабженные именем.
Описать программу - это значит указать ее заголовок и тело. В заголовке объявляют имя подпрограммы и формальные параметры. Для функции еще указывается тип возвращаемого ею результата. За заголовком следует тело подпрограммы, которое состоит из раздела описаний и раздела исполняемых операторов.
Заголовок процедуры имеет вид:
PROCEDURE <имя>[(< сп. ф. п. >)];
Заголовок функции:
FUNCTION<имя> [(< сп. ф. п.>)]: <тип>,
где <имя> - имя подпрограммы;
<сп. ф. п.> - список формальных параметров;
<тип> - тип возвращаемого функцией результата;
Список формальных параметров необязателен и может отсутствовать. Если же он есть, то в нем должны быть перечислены их имена и тип:
PROCEDURE SB (a : real; b : integer; c : char );
Операторы тела подпрограммы рассматривают список формальных параметров как своеобразное расширение раздела описаний: все переменные из этого списка могут использоваться в любых выражениях внутри подпрограммы.
Вызов и выполнение осуществляется при помощи оператора процедуры:
<имя процедуры>(<список фактических параметров>);
Между формальными и фактическими параметрами должно быть полное соответствие, т.е. должно быть одинаковое количество, порядок их следования должен быть один и тот же, тип каждого фактического параметра должен совпадать с типом соответствующего ему формального параметра. Определение формального параметра тем или иным способом существенно только для вызывающей программы: если формальный параметр объявлен как параметр-переменная, то при вызове подпрограммы ему должен соответствовать фактический параметр в виде переменной нужного типа; если формальный параметр объявлен как параметр-значение, то при вызове ему может соответствовать произвольное выражение. Контроль над неукоснительным соблюдением этого правила осуществляется компилятором языка Turbo Pascal.
Расмотрим взаимодействие основной программы с процедурами и функциями.
Program
Const
MWSt = 14.0;
Var
Value, cost:real;
Procedure Input_number (var Input_value:real);
{данная процедура решает задачу ввода стоимости товара после предварительного запроса }
Begin
Write(‘Ведите, велечину стоимости товара: ’)
Readln (Input_value);
End;
Prodcedure Calulation_cost (Cost,Value:real);
{данная процедура позволяет вычислить велечину цены ,учитывая при этом велечину налога}
Begin
Cost:=(1.0+MWSt/100.0)*Value;
End;
Procedure Output_result (Input_value:real);
{данная процедура позволяет вывести на экран результаты расчетов}
Begin
Writeln;{Оператор Writeln заданный без параметров,}
Writeln;{Переводит курсор на начало следующей строки}
Writeln(‘Расчетная цена с учетом’,MWSt:5:2,’% налога’,’составляет: ’,Cost:7:2,’ $.’);
End;
Begin {Основной блок программы}