ВУЗ: Пермский национальный исследовательский политехнический университет
Категория: Лекция
Дисциплина: Программирование
Добавлен: 19.10.2018
Просмотров: 5030
Скачиваний: 11
СОДЕРЖАНИЕ
1.2.Описание стандартных типов данных
Вычисление выражений с использованием стандартных функций
Вычисление выражений с использованием стандартных функций.
Описание используемых стандартных функций.
2.1. Составной и пустой операторы.
Решение уравнений и неравенств с использованием условного оператора.
Лабораторная работа № 2, вариант № 8.
Решение уравнений и неравенств с использованием условного оператора.
Лабораторная работа № 3, вариант № 8.
Организация циклов в программе.
Лабораторная работа № 4, вариант № 8.
Организация циклов в программе.
3.3. Метод половинного деления.
Лабораторная работа № 5, вариант № 3.
Решение нелинейных уравнений методом итераций.
Распечатка результатов работы программы в следующем виде:
Лабораторная работа № 5, вариант № 3.
Решение нелинейных уравнений методом Ньютона.
Распечатка результатов работы программы в следующем виде:
Лабораторная работа № 5, вариант № 3.
Решение нелинейных уравнений методом половинного деления.
Описание метода половинного деления:
Блок-схема метода половинного деления:
Распечатка результатов работы программы в следующем виде:
Метод Монте-Карло (метод статистических испытаний)
5.2.2. Классы задач по обработке массивов.
5.2.2.1. Однотипная обработка всех или указанных элементов массивов.
5.2.2.2. Задачи, в результате решения которых изменяется структура массива.
5.2.2.3. Обработка нескольких массивов одновременно.
5.2.2.4. Поисковые задачи для массивов.
5.2.2.5.1. Сортировка вставкой
5.2.2.5.3. Сортировка обменом («пузырьковая сортировка»)
5.2.2.5.4. Сортировка фон Неймана (слиянием)
5.3.1. Описание двумерных массивов.
5.3.2. Сортировка двумерных массивов
6.2. Процедуры обработки строк.
Лабораторная работа № 7, вариант № 8.
7. Комбинированные типы. Оператор присоединения
Работа с комбинированными типами данных.
Лабораторная работа № 8, вариант № 8.
Работа с комбинированными типами данных.
Работа с множественными типами данных.
Лабораторная работа № 9, вариант № 3.
Input_number (Value);
Calculation_cost (Cost,Value);
Output_result (Cost);
End.
На примере сложения двух чисел проиллюстрируем возможности ТП 7.0 по оформлению программ при помощи процедур и функций.
Program
{Программа демонстрирует различия между процедурами и функциями.}
Uses Crt;
Var
a,b,Sum_numbers : integer;
Prosedure Summing_up (Var sum : integer; a,b : integer);
Begin
Sum := a + b ;
End;
Function Sum(a ,b : integer) : integer;
Begin
Sum := a + b ;
End;
Begin
Clrscr;
a:= 12;
b:= 15;
{Сумма чисел с использованием процедуры}
Summing_up (Sum_numbers, a, b);
Writeln(‘Сумма чисел равна: ’,Sum_numbers);
{Сумма чисел с использовнием функции}
Sum_numbers := Sum(a , b);
Writeln(‘Сумма чисел равна: ’,Sum_numbers);
Writeln(‘Сумма чисел равна: ’, Sum(a, b));
End.
5.2. Одномерные массивы.
5.2.1. Описание массивов.
Массив – это формальное объединение нескольких однотипных объектов (чисел, символов, строк и т.п.), рассматриваемое как единое целое.
Массив описывается следующим образом:
<имя_типа> = ARRAY [<сп_инд_типов>] OF <тип>,
где ARRAY, OF – зарезервированные слова (массив, из);
<имя_типа> -- правильный идентификатор;
<сп_инд_типов> -- тип-диапазон, с помощью которого компилятор определяет число элементов массива.
<тип> -- любой тип ТР, в том числе и другой массив.
Определить переменную как массив можно непосредственно при описании этой переменной, без предварительного описания типа массива, например:
var f : array [1..12] of integer.
5.2.2. Классы задач по обработке массивов.
Перечисленные ниже классы задач относятся как к одномерным, так и к двумерным массивам.
Классы задач:
-
Однотипная обработка всех или указанных элементов массива.
-
Задачи, в результате решений которых изменяется структура (порядок следования элементов) массива.
-
Обработка нескольких массивов одновременно. Сюда же относятся задачи, когда по-разному обрабатываются подмассивы одного и того же массива.
-
Поисковые задачи для массивов.
-
Сортировка массивов.
5.2.2.1. Однотипная обработка всех или указанных элементов массивов.
Решение задач первого класса сводится к установлению того, как обрабатывается каждый элемент массива или указанные элементы. Затем выбирается подходящая схема перебора элементов, в которую вставляются операторы обработки элементов массива.
Пример: Найти максимальный (минимальный) элемент массива
Решение:
const n = 30;
var a: array [1..n] of integer;
i, max: integer;
begin
for i: = 1 to n do
read (a[i]);
max: = a[1];
for i: = 2 to n do
if a [i] > max then max: = a [i];
writeln (‘максимальный элемент массива равен ‘ , max)
end.
5.2.2.2. Задачи, в результате решения которых изменяется структура массива.
Особенностью задач этого класса является изменение порядка следования элементов массива. Для этого часто приходится менять местами элементы массива. Для чего необходимо ввести дополнительную переменную, для того, чтобы не потерять старое значение элемента массива. Это выполняется с помощью приведенных ниже операторов.
Пример: Поменять местами пары соседних элементов, т.е. первый и второй, третий и четвертый и т.д. (n-1)-ый и n-ый
Решение:
i: = 2
while i < n do
begin
r: = a[i];
a[i]: = a[j];
a[j]: = r;
i: = i + 2
End.
5.2.2.3. Обработка нескольких массивов одновременно.
Если обрабатываются несколько массивов одновременно, то для каждого массива нужно выбрать подходящую схему перебора, завести свой индекс, следить , чтобы индекс не вышел за границы массива. В некоторых частных случаях для обработки нескольких массивов бывает достаточно одного индекса, потому что элементы массива обрабатываются «синхронно», то есть, зная индекс элемента одного массива, можно вычислить по некоторой формуле индекс соответствующего ему элемента другого массива. Если такой формулы установить не удается, то говорят, что массивы обрабатываютя «асинхронно».
Пример: Дан массив целых чисел. Необходимо сформировать второй массив, содержащий четные элементы первого массива, при этом расположить элементы во втором массиве:
а) на тех же позициях, что и в первом;
б) сдвинуть к началу массива.
Решение:
Вариант 1:
const nn = 30;
var a, b: array [1..n] of integer;
i, n: integer;
begin
write (‘задайте количество элементов массива’);
readin (n);
for i: = 1 to n do
begin
read (a[i]);
if a[i] mod 2 = 0 then b[i]: = a[i];
End;
for i: = 1 to n do
write (b[i],”);
End.
Вариант 2.
const nn = 30;
var a, b: array [1..n] of integer;
i, k, n: integer;
begin
write (‘задайте количество элементов массива’);
readln (n);
for i: = 1 to n do
read (a[i]);
k: = 0; {в массиве b нет ещё элементов}
for i: = 1 to n do
if a[i] mod 2 = 0 then begin
k: = k + 1;
b[k]: = a[i];
end;
for i: = 1 to k do
write (b[i], “);
End.
5.2.2.4. Поисковые задачи для массивов.
Часто в программировании возникает задача отыскать первый элемент, совпадающий с заданным х. Для решения этой задачи могут быть предложены следующие варианты:
- линейный поиск;
поиск с барьером;
дихотомический поиск.
Линейный поиск
Алгоритмом такого поиска был рассмотрен при решении типовых задач на построение циклических алгоритмов. Напомним, что особенностью такого поиска является две причины прекращения поиска:
Элемент найден (это программируется с помощью логической переменной)
Просмотрены все элементы, но заданный элемент так и не нашли
(i > n)
const n = 20; {количество элементов в массиве}
var a: array [1..n] of integer; {исходный массив}
i, x: integer;
f: boolean;
begin
write (‘задайте искомый элемент’);
readln (x);
writeln (‘задайте элементы массива’);
for i: = 1 to n do
readln (a[i]);
f: = false; {элемент ещё не найден}
i: = 1;
while (i < = n) and not f do
if a[i] = x then f: = true {нашли}
else i: = i + 1 {переходим к следующему элементу}
if f then writeln (‘ нашли элемент с номером‘, i)
else writeln (‘такого элемента нет’)
End.
Поиск с барьером
Применяется широко распространенный прием фиктивного элемента, или барьера, расположенного в конце массива. Использование барьера позволяет упростить условие окончания цикла, т.к. заранее ясно, что хотя бы один элемент, равный а, в массиве есть. При этом необходимо увеличить размер массива на 1.
сonst n = 20; {количество элементов в массиве}
var a: array [1..n + 1] of integer; {исходный массив}
i, x: integer;
begin
write (‘задайте искомый элемент’);
readln (x);
writeln (‘задайте элементы массива’);
for i: = 1 to n do
readln (a[i]);
a[n + 1]: = x; {установлен барьер, равный х, в конце}
i: = 1; {массива}
while a[i] <> x do
i: = i + 1; {переходим к следующему элементу}
if i <> n + 1 then writeln (‘нашли элемент с номером’, i)
else writeln (‘такого элемента нет’):
End.
Дихотомический поиск (поиск элемента в упорядоченном массиве)
Алгоритм дихотомического поиска достаточно прост. Делим массив пополам и определяем в какой из частей может находиться искомый элемент. Поскольку массив упорядочен, то сравнивая искомый элемент со средним элементом массива, легко определить интересующую нас половину. Затем выбранную половину опять делим пополам и определяем в какой половине находится искомый элемент. Этот процесс продолжаем до тех пор, пока не будет найден искомый элемент, либо левая граница нового отрезка не станет больше правой. В последнем случае можно сделать вывод о том, что искомого элемента в массиве нет.
const n = 20; {kоличество элементов в массиве}
var a: array [1..n] of integer; {исходный массив}
i, x, k, m: integer;
left, right, mid: integer: {левая, правая граница и середина}
f: boolean; {отрезка}
begin
write (‘задайте искомый элемент’);
readln (k);
for i: = 1 to n do
readln (a [i]);
{упорядочивание массива по возрастанию}
for i: = 1 to n – 1 do
begin
m: = i;
for j: = i + 1 to n do
if a[j] < a[m] then m: =j;
x: = a[i];
a[i]: = a[m]; a[m]: = x
end;
{поиск элемента}
f: = false; {элемент не найден}
left: = 1; right: = n;
repeat {поиск элемента в части массива от элемента [left] до
элемента [rigth]}
mid: = (left + right) div 2;
if k < a[mid] then right: = mid – 1 {элемент в левой части}
else if k > a[mid] then left: = mid + 1 {элемент в правой части}
else f: = true; {нашли}
else f: = true; {нашли}
until f or (left > rigth);
if f then writeln (‘элемент с номером’, mid: 2, ‘совпадает с
исковым’, k)
else writeln (‘не нашли’);
End.
5.2.2.5. Сортировка массивов.
5.2.2.5.1. Сортировка вставкой
Массив разделяется на две части: отсортированную и неотсортированную. Элементы из неотсортированной части поочередно выбираются и вставляются в отсортированную часть так, чтобы не нарушить в ней упорядочность элементов.
В начале работы алгоритмы в качестве отсортированной части массива принимают только один первый элемент, а в качестве неотсортированной части – все остальные элементы.
Таким образом, алгоритм будет состоять из n – 1-го прохода (n – размерность массива), каждый из которых будет включать четыре действия:
Взятие очередного i-го неотсортированного элемента и сохранение его дополнительной переменной.
Поиск позиции j в отсортированной части массива, в которой присутствие взятого элемента не нарушит упорядоченности элементов.
Сдвиг элементов массива от i – 1-го до j-го вправо, чтобы освободить найденную позицию вставки.
Вставка взятого элемента в найденную j-ю позицию.
1 шаг:
шаг:
-
 3
31
9
2
5
7



-
1
2 шаг:
шаг:
-

 1
13
9
2
5
7
-
9
3 шаг:
шаг:
-

 1
13
9
2
5
7
-
2
4 шаг:
шаг:
-
 1
12
3
9
5
7

-
5
5 шаг:
шаг:
-
 1
12
3
5
9
7

-
7
Результат:
-
1
2
3
5
7
9
БЛОК – СХЕМА
I = 2



1



J = 1 R = A(I) IR =





 1
1






I = I + I




IR = 1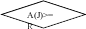
 1
1






K = I - 1 J = J+1







 1
1




A(J) = R IR = 2
A(K+1) = A(K) K = K - 1











Программа, реализующая рассмотренный алгоритм, будет иметь следующий вид.
Program Insertion Sort;
Uses Crt;
Const
n =10; {длина массива}
type
TVector = array 1…n of Real;
Var
Vector : TVector;
B : Real;
i, j, K : Integer;
Begin
ClrScr;
Writeln (‘Введите элементы массива:’);
For i:=1 to n do Read (Vector i); Readln;
{- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - }
for i:=2 to n do
begin
B:=Vector i; {взятие неотсортированного элемента}
{цикл поиска позиции вставки}
j:=1
While (BVector j ) do
j:= j+1 {после окончания цикла индекс j фиксирует позицию}
{вставк} {цикл сдвига элемента для освобождения позиции вставки}
for K:= i-1 downto j do
Vector K+1: = Vector K;
{Вставка взятого элемента на найденную позицию}
Vector j: = B;
End;
{ - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - }
Writein (‘Отсортированный массив:’);
For i: = 1 to n do write (‘vector [i] : 8 : 2);
Writeln;
End.
Результат работы :
|
7654098321 Отсортированный массив : 0123456789 |
5.2.2.5.2. Сортировка выбором
Находим (выбираем) в массиве элемент с минимальным значением на интервале от 1-го элемента до n-го (последнего) элемента и меняем его местами с первым элементом. На втором шаге находим элемент с минимальным значением на интервале от 2-го до n-го элемента и меняем его местами со вторым элементом. И так далее для всех элементов до n-1-го.
1

 шаг:
шаг:
-
5
11
3
7
1
4
2
9
min


2 шаг:
шаг:
-
1
11
3
7
5
4
2
9
min
3


 шаг:
шаг:
-
1
2
3
7
5
4
11
9
min
4

 шаг:
шаг:
-
1
2
3
7
5
4
11
9
min
5


 шаг:
шаг:
-
1
2
3
4
5
7
11
9
min
6


 шаг:
шаг:
-
1
2
3
4
5
7
11
9
min
7

 шаг:
шаг:
-
1
2
3
4
5
7
11
9
min
Результат:
-
1
2
3
4
5
7
9
11
БЛОК – СХЕМА
I = 1

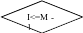


1




J = I L = 1



 1
1




R = A(L) F(L) =A(I) A(I) = R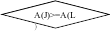 1
1