входные параметры:

1) Mas типа Vector - вектор, элементы которого необходимо суммировать.

2) N типа Integer - размерность вектора, не может превышать 100}

Var

I, S : Integer;

Begin

S:=0;

For I:=l to N do S:=S+Mas[I];

Sum_V:=S;

End;

{Основная программа}

Begin

Repeat

Write('Введите размерность массива');

Readln(K);

Until (K>=1)And(K<=100);

InpVec(A , K);

Writeln(‘Сумма элементов массива А = ‘, Sum_V(A, K));

End.

Приведем теперь простые примеры использования подпрограмм-процедур и подпрограмм-функций.

Примеры решения задач с использованием процедур и функций

Пример 4.1. Составить программу для определения зна­чений n!, m!, (n-m)!, используя функцию при вычислении факториала.

Решение.

Программа имеет вид:

Program Prim41;

Var

N, M, NF, MF, NMF : Integer;

Function FACT(K : Integer) : LongInt;

Var PF, I : Integer;

Begin

PF := 1;

For I:=1 TO К Do

PF := PF*I;

FACT:= PF

End;

Begin

Write(‘Введите N и M’);

Readln(N, M);

NF := FACT(N);

MF:= FACT(M);

NMF:= FACT(N-M);

Writeln('HF= ',NF,' HF= ', MF,' NHF= ',NMF)

End.

В операторах присваивания программы записаны три обращения к функции FACT (N), FACT (M), FACT (N—M).

Пример 4.2. Составить программу для вычисления значения функции y=ax²+bx+d, где

; ; ,

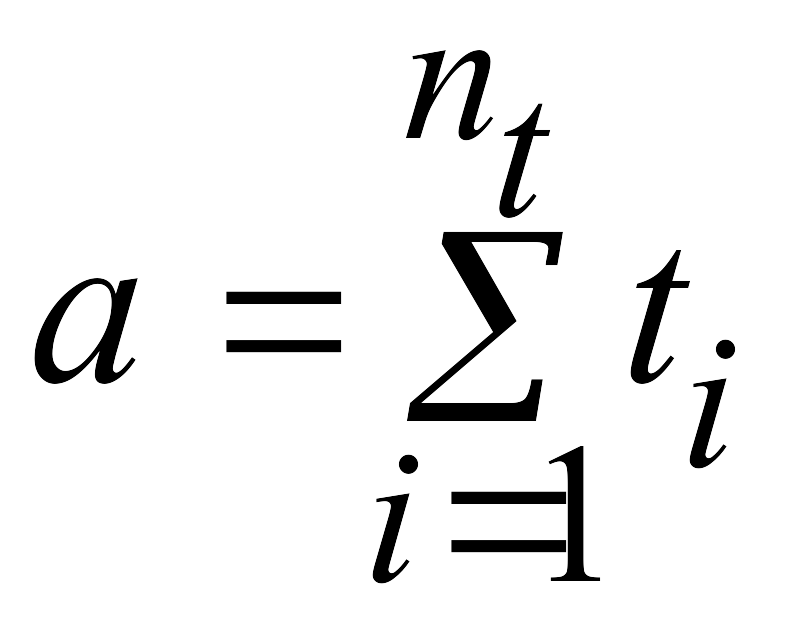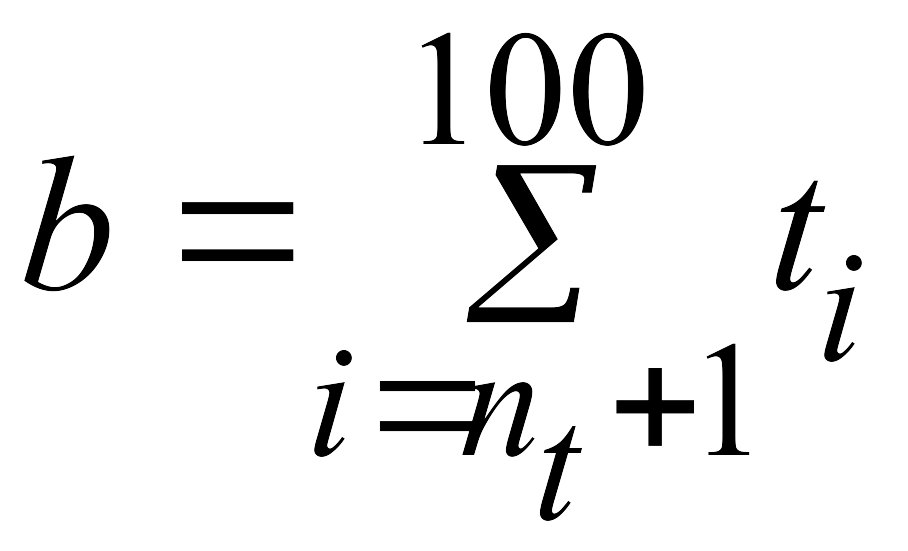используя функцию SUM.

Решение.

Программа имеет вид:

Program Prim42;

Const N = 100;

Type

INDEX = 1..N;

VECT = Array[INDEX] Of Real;

Var

I, NТ : Integer;

T,Q : VECT;

X,Y : Real;

Function SUM (MAS : VECT; K : Integer; MM : INDEX) : Real;

Var J : Integer; S : Real;

Begin

S := 0;

For J:= 1 To MM DO

S := S+MAS[J];

SUM := S

End;

Begin

Write(‘Введите Nt ’);

Readln(NT);

For I:=1 To N DO Read(T[I]);

For I:=1 TO 20 DO Read(Q[I]);

Y:=SUM(T, 1, NT)*X*X + SUM(T, NT+1, N)*X + SUM(Q, 1, 20) ;

Write(‘Y: = ', Y)

End.

Указание. Несмотря на то что обрабатываемые массивы имеют разную длину, они описываются в программе как массивы одного и того же типа (VECTOR), так как при обращении к процедуре типы соответствующих формальных и фактических параметров должны совпадать.

Пример 4.3. Составить программу вычисления функции

,

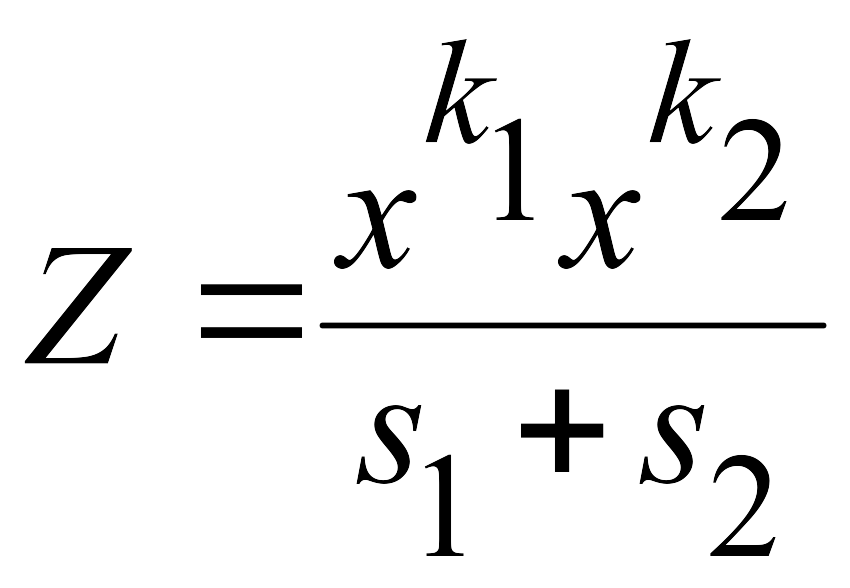где s₁ и k₁ — сумма и количество положительных элементов массива A(A₁, A₂, ..., A₇₀); s₂ и k₂ — сумма и количество положительных элементов массива B(B₁, В₂, ..., В₄₀). Для вычисления суммы и количества положительных элементов массива использовать процедуру SUMKOL, в которой вычисляются s — сумма положительных элементов массива MAS и k — количество этих элементов.

Решение.

Программа имеет вид:

Program Prim43;

Const Rasm=100;

Type

INDMAX = 1..Rasm;

Vector = Array[INDMAX] Of Real;

Var

NA, NB, I, K1, K2 : Integer;

Z, S1, S2, X : Real;

A, B : Vector;

Procedure InpVec(var Mas: Vector; N: INDMAX);

Var I: Integer;

Begin

Writeln('Введите ', N, ' чисел');

For I := 1 to N do

Read(Mas[I])

End;

Procedure SUMKOL(Var MAS : Vector; MM : INDMAX; Var S : Real; Var K : Integer);

{Процедура, в которой подсчитывается количество К и сумма S положительных элементов массива Mas.

Входные параметры:

1. Mas – одномерный массив;

2. ММ – размер массива (количество элементов массива).

Выходные параметры:

1. S – сумма положительных элементов массива Mas;

2. К – количество положительных элементов массива Mas.}

Var J : Integer;

Begin

S := 0;

K := 0;

For J:= 1 To MM Do

If MAS[J] > 0 Then

Begin

S := S + MAS[J];

K := K + 1;

End;

End;

Function St(Y: Real; N : Integer) : Real;

{Функция, вычисляющая через умножение возведение вещественного числа Y в целую степень N, т.е. Y^N}

Var I : Integer;

P, AY : Real;

Begin

AY := ABS(Y);

P := 1;

For I := 1 To N Do P := P*AY;

If Z >=0 Then St := P

Else St := 1/P;

End;

Begin

Write(‘Введите размер массива А ‘);

Readln(NA);

InpVec(A, NA);

Write(‘Введите размер массива B ‘);

Readln(NB);

InpVec(B, NB);

SUMKOL(A, NA, S1, K1);

SUMKOL(B, NB, S2, K2);

Write(‘Введите Х: ‘);

Readln(X);

Z := St(X, K1)*St(X, K2) / (S1 + S2);

Writeln(‘Z= ', Z);

End.

Пример 4.4. Написать программу, которая в первой вводимой с клавиатуры строке подсчитывает количество точек, а во второй – количество букв “я”.

Решение.

Возможный вариант программы:

Program Prim44;

Var

St1, St2 : String;

Function KOL(S : String; Sim : Char): Integer;

Var I, K : Integer;

Begin

K := 0;

For I := 1 To Length(S) Do

If S[I] = Sim Then K := K + 1;

KOL := K

End;

Begin

Writeln('Введите первую строку');

Readln(St1);

Writeln('Введите вторую строку');

Readln(St2);

Writeln('Количество точек = ',KOL(St1, '.'));

Writeln('Количество букв я = ',KOL(St2, 'я'))

End.

Пример 4.5.Вычислить значения многочлена

F(x) = 1.5 х⁷ - 2x⁶ – 7x⁵ + 3.4x⁴ + 8x³ – 0.5x² + 5.4x - 4

при x, изменяющемся от 0 до 1 с шагом 0.1, пользуясь схемой Горнера

F(x) ==(... ((а₀x + a₁) х + а ₂) х + a ₃) х )+...+a _n.

Значения аргумента х и функции F(x) занести в массивы Х в Y соответственно и вывести на экран. Вычисление F(x) офор­мить в виде функции.

Решение.

Программа

Program Prim45;

Type

Vector = Array[0..7] Of Real;

Const

{Типизированная константа-массив}

A : Vector = (1.5, -2, -7, 3.4, 8, -0.5, 5.4, -4);

Var

X, Y : Array[1..11] Of Real;

I : Integer;

Function Gorner(B : Vector; Z : Real; N : Integer):Real;

{Параметры функции:

В - массив коэфициентов полинома;

Z - аргумент;

N - степень полинома}

Var

J : Integer;

S : Real;

Begin

S := B[0];

For J := 1 To N Do

S := S*Z + B[J];

Gorner := S;

End;

Begin

Writeln('X F(X)');

Writeln('_____________');

For I := 1 To 11 Do

Begin

{Заполнение и вывод массивов X и Y}

X[I] := 0.1*(I-1);

Y[I] := Gorner(A, X[I], 7);

Writeln(X[I]:4:2, Y[I]:9:4);

End;

End.

Контрольные вопросы

1. В каких случаях целесообразно применять процедуры и функции?

2. Какова структура описания процедур и функций?

3. Какой вид имеют заголовки процедуры и функции?

4. В чем состоит отличие описания функции от описания процедуры?

5. Можно ли для упорядочения по возрастанию массива вместо процедуры использовать функцию?

6. Какие параметры называются формальными и какие – фактическими?

7. Какие способы передачи параметров реализованы в Турбо Паскале?

8. Как происходит в программе обращение к процедуре?

9. Как происходит в программе обращение к функции?

10.Как и куда осуществляется выход из подпрограммы?

Задачи I уровня

В следующих задачах необходимо со­ставить программу, содержащую функцию.

1. Вычислить сумму значений функций

Y = F(a, b) + F(a², b²) + F(a² – 1, b) + F(a – b, b) + F(a² + b², b² –1),

где

u ² + t ², если u > 0; t > 0;

u + t, если u ≤ 0, t ≤ 0;

F(u, t) = u – t, если u > 0, t ≤ 0;

u + t, если u ≤ 0, t > 0.

2. Вычислить сумму значений функций

Y = F(sin(a), a) + F(cos(a), a) + F(sin ² (a), a - 1)+ F(sin(a)–cos(a), a ²- 1),

г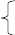 де

u + sin(t), если u > 0;

F(u, t) = u + t, если u ≤ 0.

3. Вычислить сумму значений функций

Y = F(sin(a)+cos(b), a+b)+F(sin(a), cos(b))+ F(a –b, a) + F(sin ²(a) – 2, a),

где

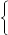u + t, если u > 1;

F(u, t) = u – t, если 0 ≤ u ≤ 1;

t - u, если u < 0.

4. Получить таблицу значений функции y = e^xsinx при x, изменяющемся от 0 до 2π с шагом π/10. Вычисление значений функции оформить в виде функции. Результаты представить в виде таблицы.

5. Получить таблицу значений функции у = (sin x)/x при x, изменяющемся от π до 2π с шагом π/10. Вычисление значений функции оформить в виде функции. Результаты представить в виде таблицы.

6. Получить таблицу значений функции y = tg х при x, изменяющемся от -π до π с шагом π/5. Вычисление значений функции оформить в виде функции. Результаты представить в виде таблицы.

7. Получить таблицу значений функции y = 2x² + x+-4 при x, изменяющемся от -5 до 5 с шагом 1. Вычисление значений функции оформить в виде функции. Результаты представить в виде таблицы.

8. Получить таблицу значений функции y = sh x при x, изменяющемся от -1 до 1 с шагом 0.1. Вычисление значений функции оформить в виде функции. Результаты представить в виде таблицы. Функция гиперболический синус определяется формулой .

9. Получить таблицу значений функции y = ch x при x, изменяющемся от -1 до 1 с шагом 0.1. Вычисление значений функции оформить в виде функции. Результаты представить в виде таблицы. Функция гиперболический косинус определяется формулой .

10. Получить таблицу значений функции y = th x при x, изменяющемся от -1 до 1 с шагом 0.1. Вычисление значений функции оформить в виде функции. Результаты представить в виде таблицы. Функция гиперболический тангенс определяется формулой .

11. Два треугольника заданы длинами своих сторон а, b и с. Вычислить площади треугольников по формуле Герона и опреде­лить наибольший из них.

12. Два треугольника заданы координатами своих вершин A(x₁, y₁), B(x₂, y₂) и С(x₃,у₃). Вычислить площади треугольни­ков и определить, который из них больше. Площадь треугольника вычислять по формуле Герона:

S =.

13. Футболист ударом ноги посылает мяч вертикально вверх с высоты 1 м с начальной скоростью 20 м/с. На какой высоте мяч будет через 1 , 3, 4 с? Движение мяча описывается зависимостью

y(t) = у₀ + v₀t -,

где у₀ — начальная высота; v₀ — начальная скорость; t- вре­мя. Оформить вычисление y(t) в виде функции. Предусмотреть печать необходимой текстовой информации.

14. Вычислить приближенно площадь фигуры, ограниченной осью х, прямыми x = 1 и x = 3 и кривой у(х) = 1/х + 5, раз­делив интервал изменения х на 10 частей и суммируя площа­ди получившихся прямоугольников, принимая их высоту, равную значению функции в середине каждого интервала. Вычисление площади прямоугольника оформить в виде функции.

15. Счастливым считается число N из шести цифр, в которой сумма левых трех цифр равна сумме правых трех цифр. Напри­мер, 457961 : 4+5+7= 9+6+1 = 16. Найти все счастливые числа в интервале от N1 до N2 и подсчитать их количество. Выделение цифры в числе оформить в виде функции.

16. Найти все такие числа в интервале от 1 до 1000, кото­рые содержатся в последних разрядах их квадрата, например: 5² = 25, 25² = 625. Выделение последних разрядов в числе офор­мить в виде функции.

17. Число Армстронга — число, состоящее из k цифр, у кото­рых сумма k-х степеней его цифр равна самому числу. Например: 153 = 1³+5³+3³. Найти все числа Армстронга, состоящие из двух, трех и четырех цифр. Нахождение числа Армстронга оформить в виде функции.

Задачи II уровня

В следующих задачах необходимо со­ставить программу, содержащую процедуру.

1. Для каждой из двух матриц сформировать одномерные массивы, составленные из минимальных элементов столбцов.

2. В каждую из двух матриц вставить заданные числа перед мак­симальным элементом каждой строки.

3. В каждую из двух матриц вставить заданные числа после ми­нимального элемента каждого столбца.

4. Для каждой из двух матриц сформировать одномерный массив, составленный из максимальных элементов строки.

5. В каждую из двух матриц добавить по строке, в которой значения эле­ментов равны количеству отрицательных элементов в соответст­вующих столбцах.

6. В каждую из двух матриц добавить по строке, в которой значения эле­ментов равны суммам элементов соответствующего столбца.

7. В каждую из двух матриц добавить по столбцу, в котором значения эле­ментов равны количествам положительных элементов в соот­ветствующих строках.

8. Для каждой из двух матриц сформировать одномерные массивы, значения элементов которых равны суммам элементов в соответствующих строках.

9. Для каждой из двух матриц сформировать одномерные массивы, значения элементов которых равны суммам элементов в соответствующих столбцах.

10. Для каждой из двух матриц сформировать одномерные массивы, в которых значения элементов равны количествам отрицательных элементов в соответствующих строках.

11. Найти разность и произведение максимальных по модулю элементов двух матриц.

12. В каждую из двух матриц добавить по столбцу, в котором эле­менты равны суммам элементов соответствующих строк.

13. Найти среднее геометрическое и среднее арифметическое макси­мального и минимального элементов каждой из двух матриц.

14. Сформировать одномерные массивы из столбцов каждой из двух матриц, содержащих максимальные количества положительных эле­ментов.

15. Найти среднее арифметическое минимальных элементов каждой из двух матриц.

16. Сформировать одномерные массивы из строк каждой из двух мат­риц, содержащих минимальные элементы этих матриц.

17. Для каждой из двух матриц сформировать одномерные массивы, в которых значения элементов равны количествам положительных элементов в соответствующих столбцах.

18. Максимальные элементы двух матриц поменять местами. Найти среднее арифметическое максимальных элементов строк каждой из двух матриц.

19. Сформировать одномерные массивы из отрицательных элементов каждой из двух матриц.

20. Проверить, является ли произведение матриц А и В перестановочным, т.е. проверить равенство А В = В А .

21. Вычислить суммы и количества элементов, находящихся в интер­вале от p до q для матриц А и В.

22. Для каждой из двух целочисленных матриц вывести на печать элементы, кратные трем.

23. Найти суммы элементов главной диагонали матриц, равных произ­ведению А В и В А.

24. В каждой из двух матриц вычислить суммы элементов над гла­вной диагональю.

Глава 5. СОРТИРОВКА И ПОИСК

5.1. Сортировка

Очень часто на практике встречаются задачи, в которых требуется переставить элементы неупорядоченного массива, после чего они становятся упорядоченными по возрастанию или убыванию. Сортировка элементов одномерного массива – это такая перестановка его элементов, в результате которой они оказываются упорядоченными определенным образом.

Процесс упорядочивания при большом объеме данных очень трудоемок, поэтому часто прибегают к помощи компьютеров.

Проблема сортировки остро встала в связи с широким внедрением ЭВМ в бизнес, где необходимо было обрабатывать огромные массивы числовой и текстовой информации. Технические средства внешней памяти тогдашних компьютеров - накопители на магнитной ленте (НМЛ) - обеспечивали только последовательную запись и чтение информации, поэтому необходимо было упорядочивать данные для того, чтобы обеспечить их быстрый поиск.

Современные устройства внешней памяти компьютеров - накопители на магнитных дисках (НГМД) - обеспечивают прямой доступ к записанной на них информации, что в некоторых случаях организации массивов данных позволяет обходиться без сортировки, но до сих пор она остается важным аспектом вычислительной техники.

Рассмотрим задачу упорядочивания в простейшей постановке: дан числовой массив x₁, …, x_n, эле­менты которого попарно различны; требуется переставить элементы массива так, чтобы после перестановки они были упорядочены в порядке возрастания: x₁ <...<x_п.

Способы сортировки

Существует несколько способов решения задачи сортировки. Каждый из них требует выполнения различного количества операций, а следовательно, времени расчета и памяти ЭВМ, необходимой для их реализации.

Способы сортировки делятся на прямые и улучшенные. Выделим следующие виды сортировок прямым способом:

- обменом ("пузырьковая сортировка");

- выбором (выделением);

• вставкой (включением).

Улучшенные способы сортировки основываются на тех же принципах, что и прямые, с использованием оригинальных идей и рационализации для ускорения процесса преобразования массива данных.

Сортировка обменом

Одной из наиболее простых (но и наи­более медленных) является так называемая сортировка обменом пар.

Основой алгоритма является сравнение двух элементов и их переста­новка для получения порядка по возрастанию или убыванию значений элементов массива.

Для упорядочивания массива попарно различных чисел x₁, ..., x_п может быть использован алгоритм “пузырьковой” сортировки (сортировки обменами). Опишем этот алгоритм применительно к упорядочиванию по воз­растанию. На каждой итерации i=1, 2, 3, … N-1 последовательно сравниваются пары соседних элементов x_j и x_j+1 , j=1, 2, 3, …, N-i, и если x_j>x_j+1, то они переставляются. Таким образом, после каждой итерации по i наибольший элемент оказывается на своем месте в конце массива.