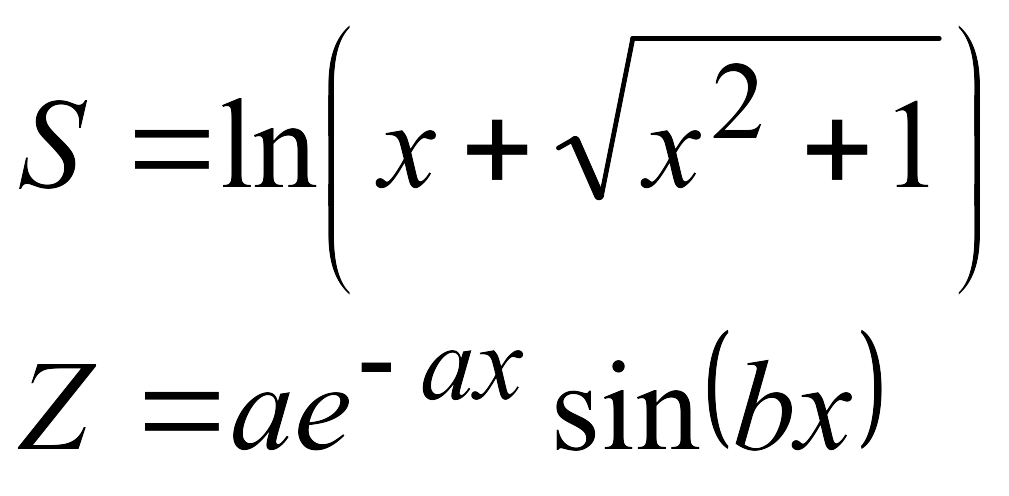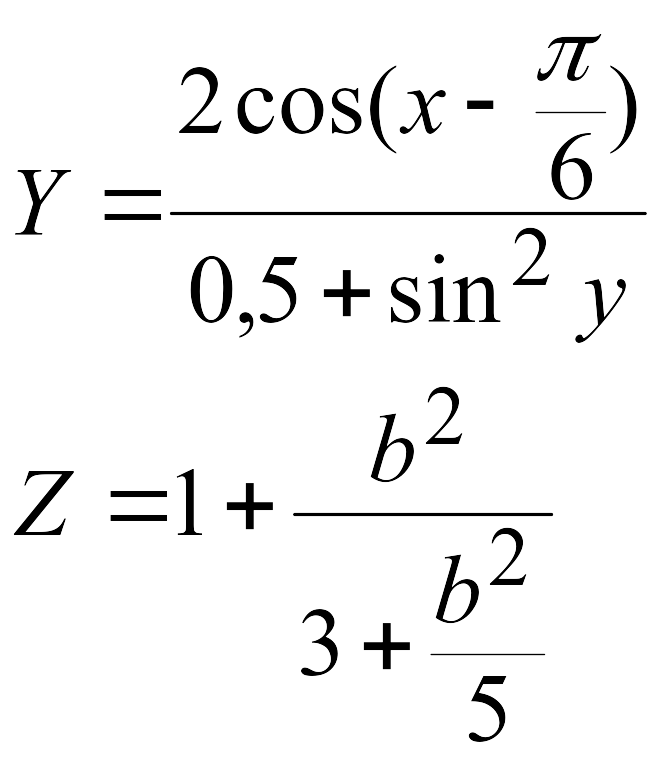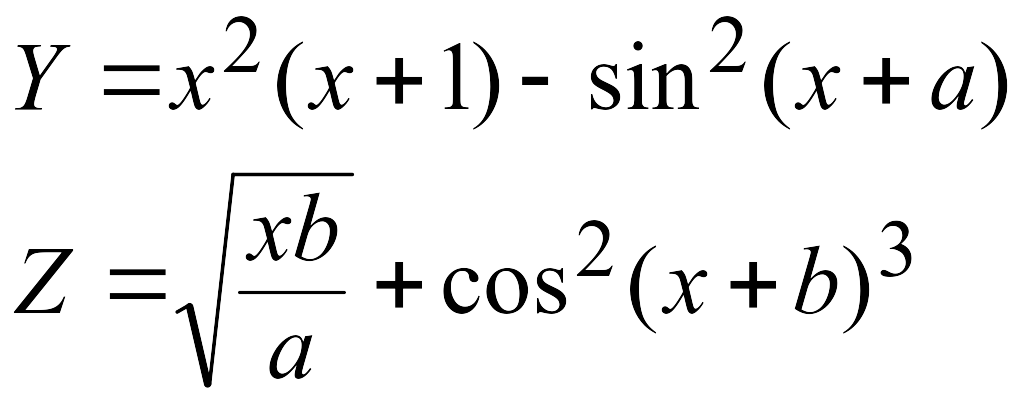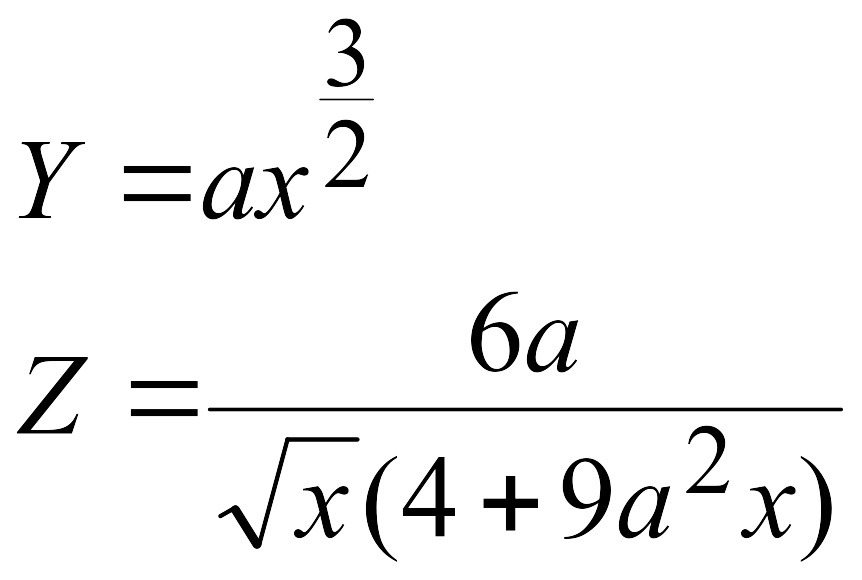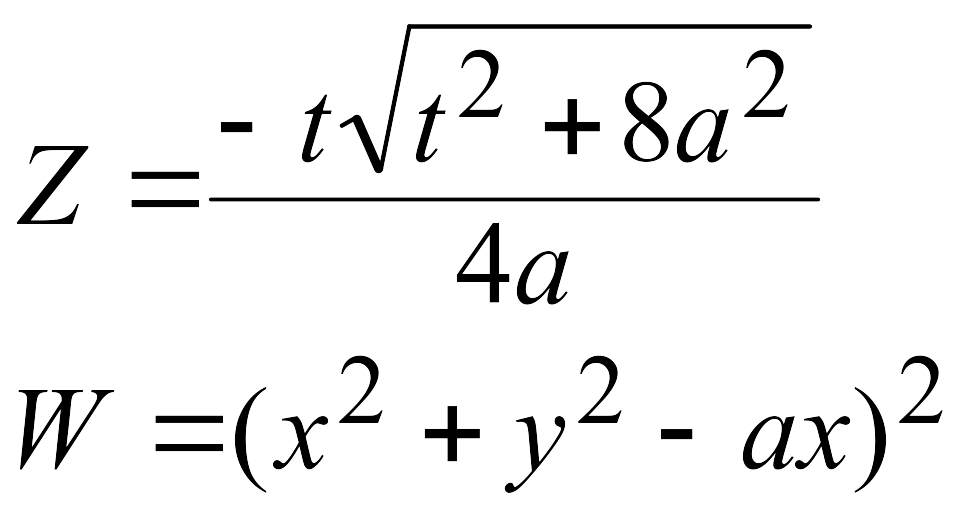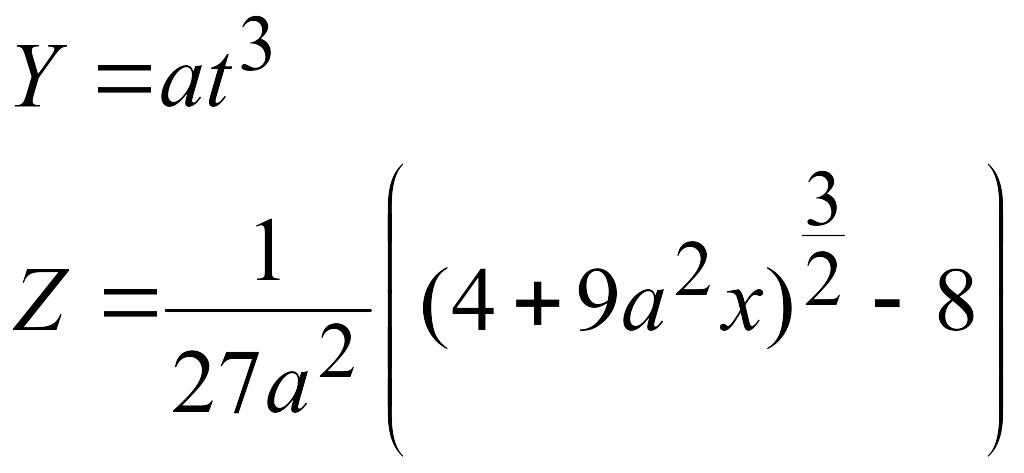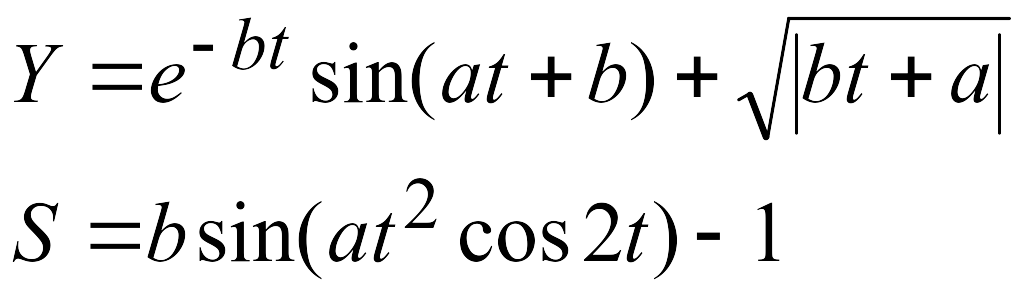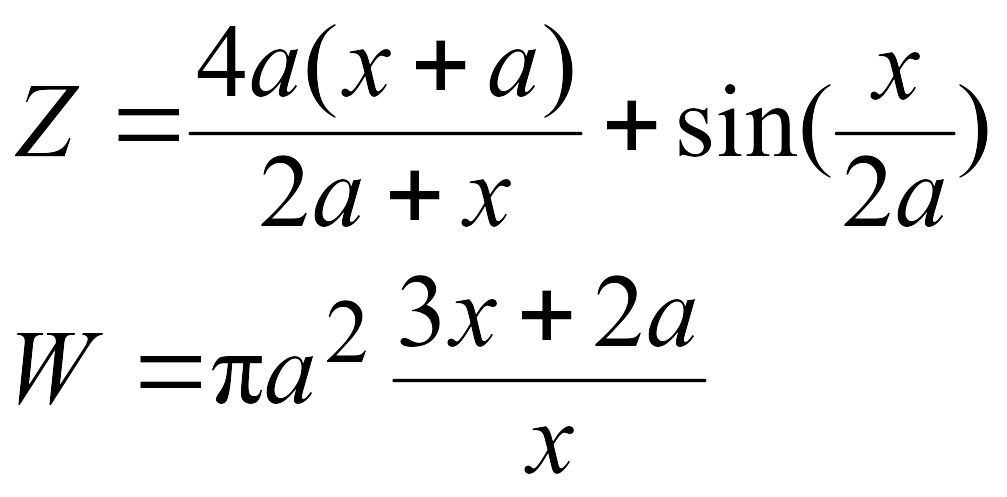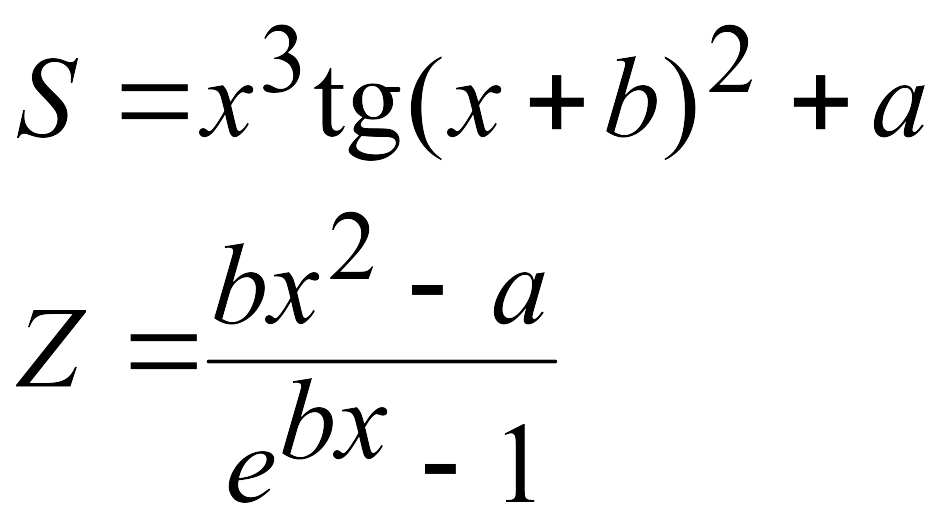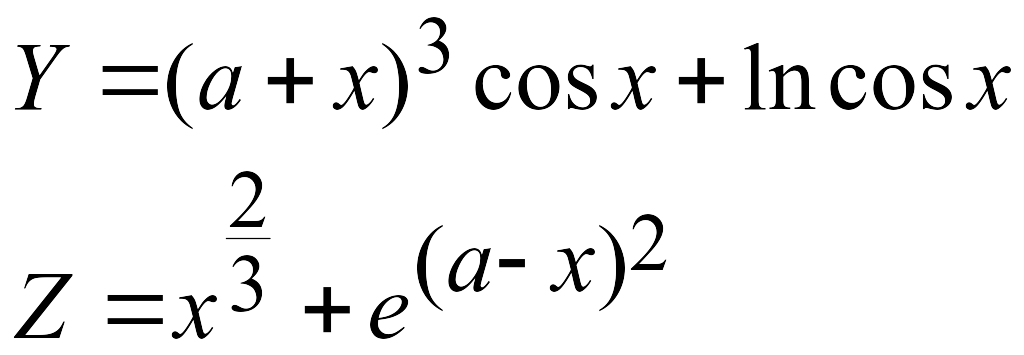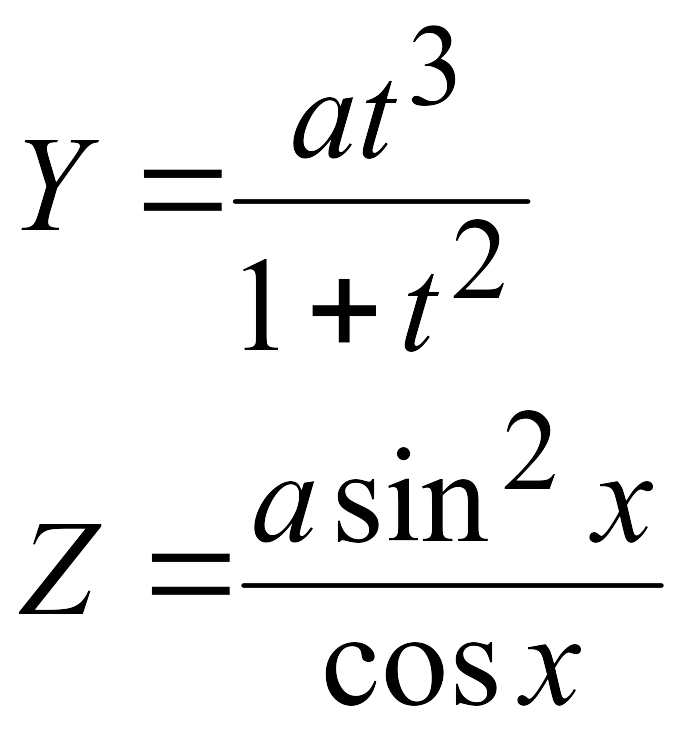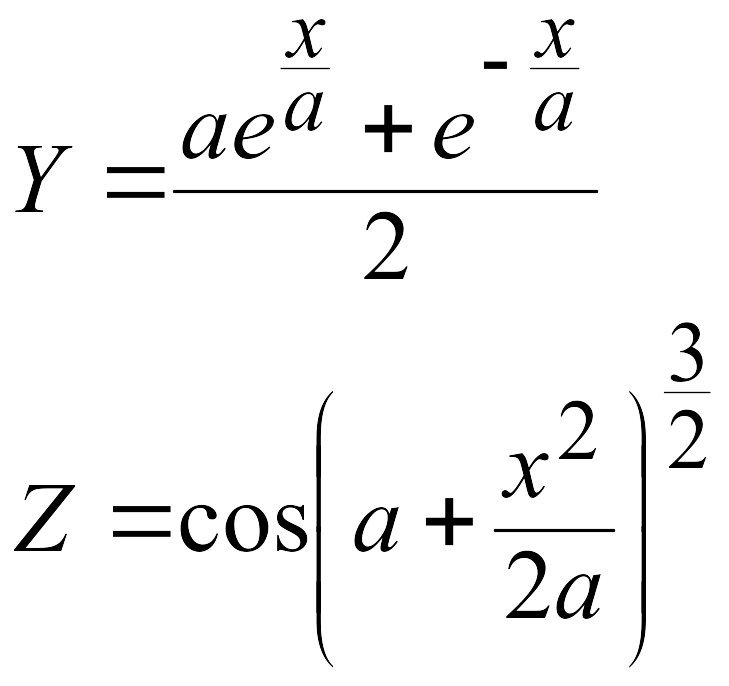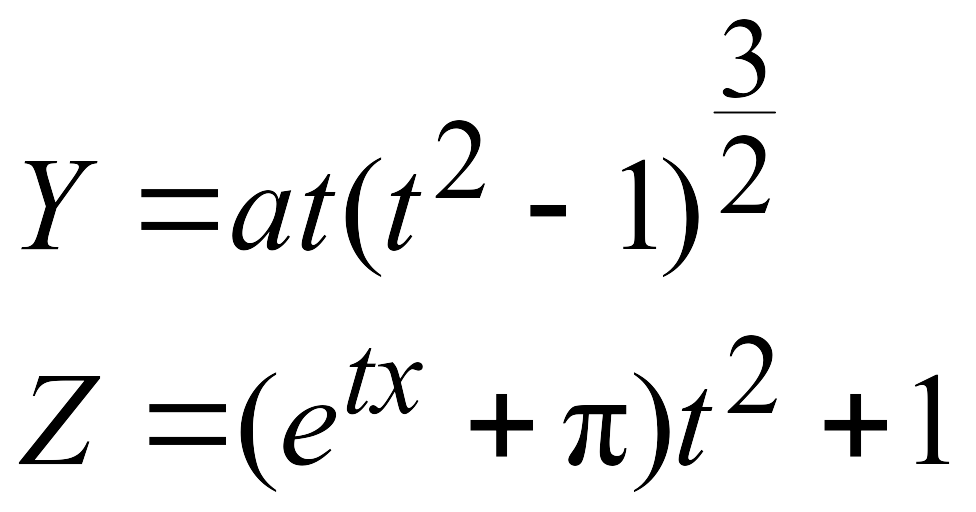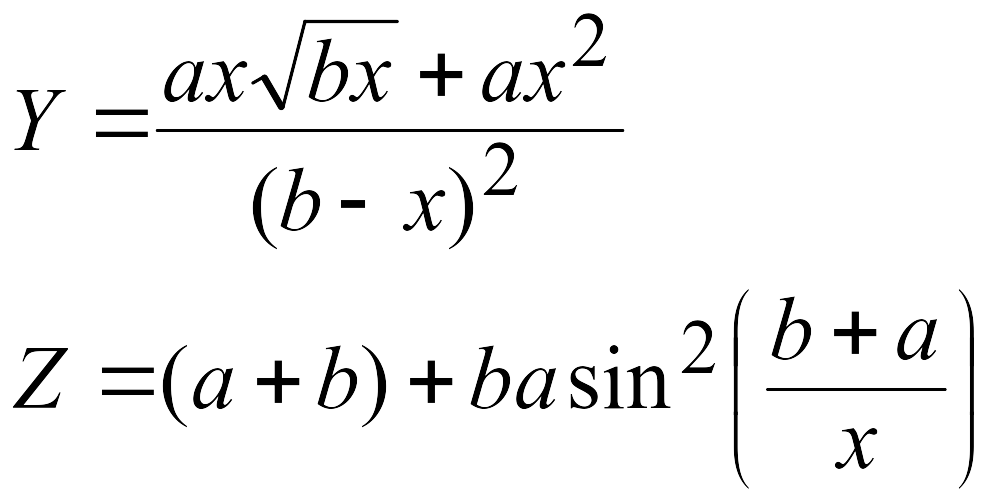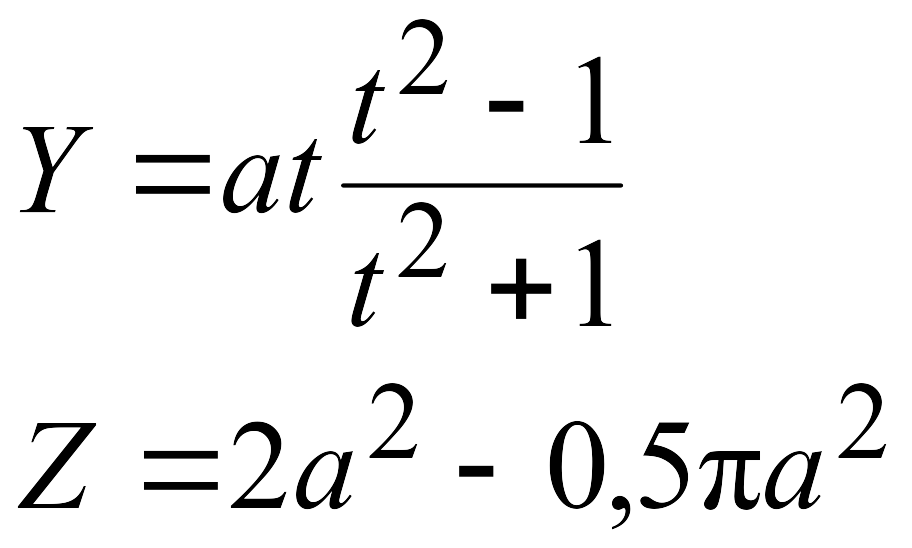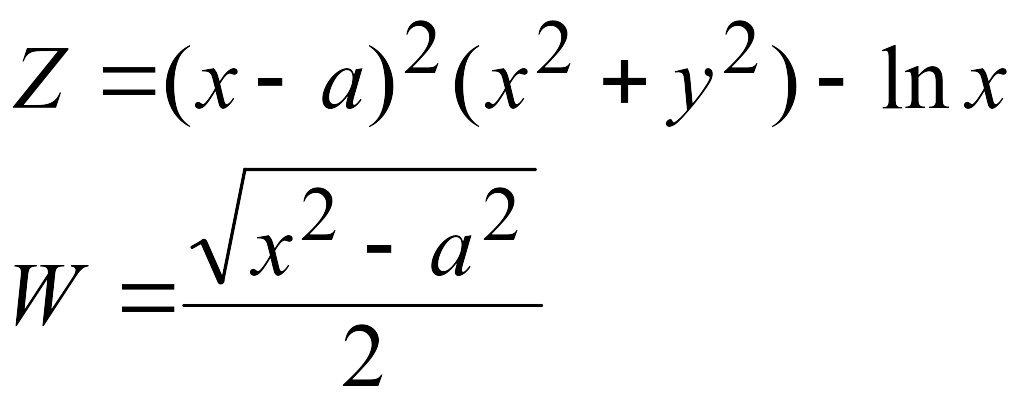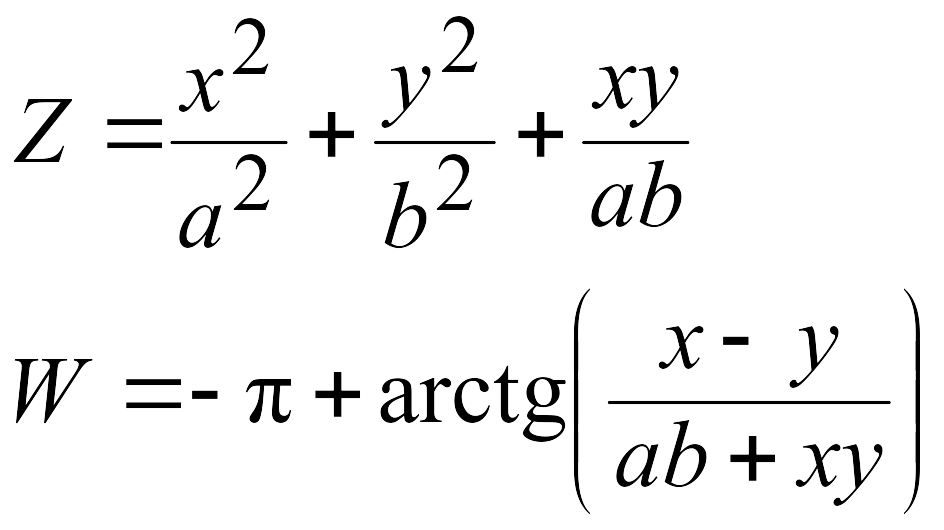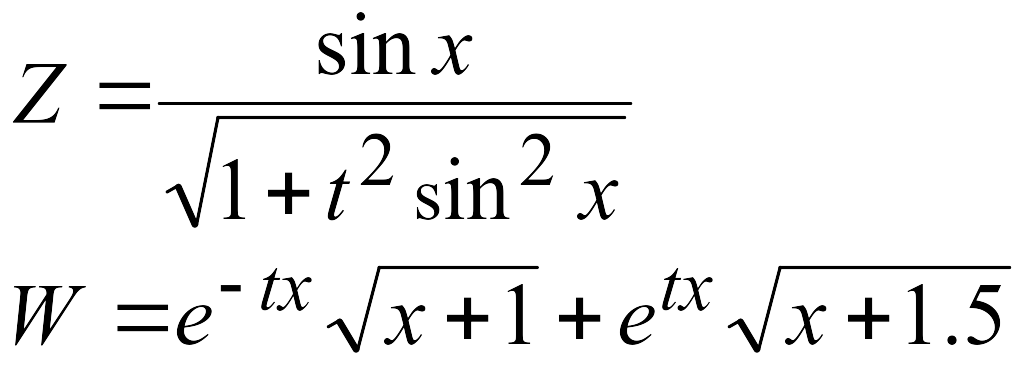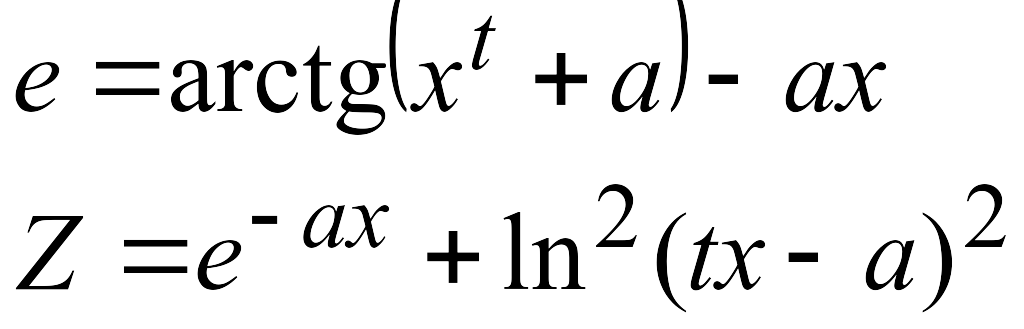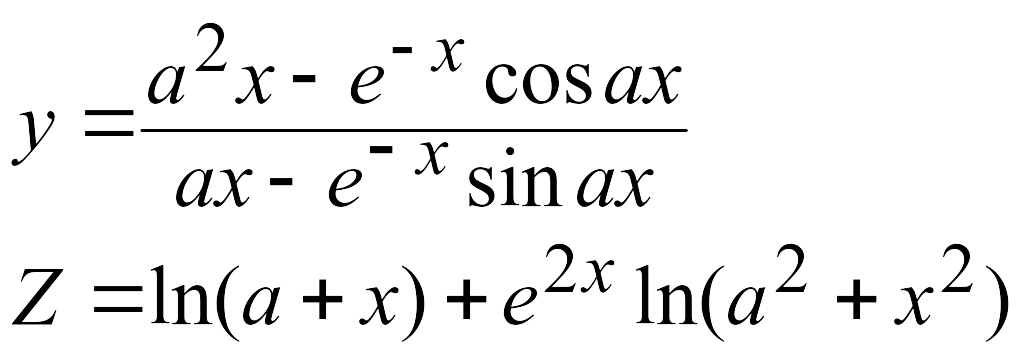Файл: Методичка к лабораторным и практическим.doc

ПРОГРАММИРОВАНИЕ

И ОСНОВЫ

АЛГОРИТМИЗАЦИИ

В ПРИМЕРАХ И ЗАДАЧАХ

ОГЛАВЛЕНИЕ

ПРЕДИСЛОВИЕ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .3

Глава1. ОСНОВНЫЕ ТИПЫ АЛГОРИТМОВ . . . . . . . . . . . . . . . . . . . . . . . .5

1. Понятие алгоритма . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ..5

1.2. Этапы разработки алгоритма . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . 6

1.3. Реализация линейных алгоритмов . . . . . . . . . . . . . . . . . . . . . . . . . . .7

1.4. Реализация разветвляющихся алгоритмов . . . . . . . . . . . . . . . . . . 14

1.5. Реализация циклических алгоритмов . . . . . . . . . . . . . . . . . . . . . . 22

Глава 2. СТРУКТУРИЗАЦИЯ ПРОГРАММНЫХ ДАННЫХ . . . . . . . . . . 46

2.1. Массивы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . .46

2.2. Строки . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . 70

2.3. Записи . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 81

Глава 3. ФАЙЛЫ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 91

3.1. Основные процедуры и функции работы с файлами . . . . . . . . . . 91

3.2. Работа с файлами . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 95

Глава 4. МОДУЛЬНОЕ ПРОГРАММИРОВАНИЕ. ПРОЦЕДУРЫ

И ФУНКЦИИ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 110

4.1. Понятие подпрограммы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .110

4.2. Процедуры и функции . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .111

Глава 5. СОРТИРОВКА И ПОИСК. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .123

5.1. Сортировка . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .123

5.2 Поиск . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 137

ЗАКЛЮЧЕНИЕ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 143

БИБЛИОГРАФИЧЕСКИЙ СПИСОК . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .144

Глава 1. ОСНОВНЫЕ ТИПЫ АЛГОРИТМОВ

1. Понятие алгоритма

Решить задачу — это значит получить результат, отвечающий целям данной задачи. Процесс решения представляет собой совокупность вполне определенных действий над исходными данными. В большинстве случаев эта совокупность действий может быть задана в виде инструкции настолько подробно, что ее исполнение становится механическим процессом. Такая инструкция называется алгоритмом.

Понятие алгоритма имеет строгое математическое определение, но мы остановимся на интуитивно-содержательном определении: алгоритмом называется последовательность точных и понятных действий (предписаний, правил, инструкций, команд) над данными, приводящая к получению результата решения любой конкретной задачи из некоторого класса однотипных задач.

Основные свойства любого алгоритма: детерминированность, означающая, что применение алгоритма к одним и тем же исходным данным должно приводить к одному и тому же результату; массовость, позволяющая получать результат при различных исходных данных; результативность, обеспечивающая получение результата через конечное число шагов.

Существует несколько способов записи алгоритмов, отличающихся друг от друга наглядностью, компактностью, степенью формализации и другими показателями. Наибольшее распространение получили способы: словесный , в виде блок-схем, в виде программ для ЭВМ.

Независимо от того, как представлен алгоритм (в виде схемы, текста или программы), его структура должна быть достаточно жесткой и вклю­чать определенные элементы.

Из теории известно, что любой алгоритм может быть реализован в виде комбинации трех базовых алгоритмических конструкций: следование, ветвление, повторение (цикл).

Конструкция следование образуется из последовательности команд, выполняе­мых друг за другом в естественной последовательности.

Ветвление осуществляет выбор одного из двух или более возможных действий в зависимости от условия.

Повторение (цикл) обеспечивает многократное выполнение одних и тех же действий для различных значений входящих в них данных.

2. Этапы разработки алгоритма

Разработка любого алгоритма состоит из нескольких тесно взаимосвя­занных этапов. На каждом из них решаются свои специфические вопросы, определяющие в конечном счете общий результат алгоритмизации решаемой задачи.

Этап анализа постановки задачи — это основа решения задачи. Имен­но на этом этапе определяются составляющие, необходимые для разработки алгоритма.

Главная цель анализа — это понять задачу. Если совершена ошибка на этом этапе, т.е. задача неверно понята, то вся последующая работа становит­ся бессмысленной.

Что значит понять задачу? Во-первых, необходимо в постановке задачи выделить и осмыслить все исходные данные и требуемые результаты. Во-вторых, необходимо сформулировать постановку задачи в виде одного короткого конкретного предложения. Чтобы предложение получи­лось коротким, необходимо в исходной постановке задачи «выбросить» все уточняющие детали.

“Сборка” алгоритма может происходить двумя путями. Во-первых, базовые конструкции могут соединяться в последовательность, образуя конструкцию следования. Это возможно, так как каждая базовая конструкция имеет один вход и один выход. Во-вторых, одна базовая конструкция может вкладываться в другую конструкцию, образуя “вложенные” конструкции. Это также возможно, так как внутри составных команд могут быть снова составные конструкции.

Таким образом, при построении алгоритм может развиваться как “вширь”, так и “вглубь” включением одних конструкций в другие. Такое конструирование обычно и происходит на практике. Алгоритм строится в несколько шагов: сначала он формулируется в самых общих чертах, а затем уточняется путем детализации более крупных через более мелкие. На каждом шаге алгоритм расширяется по мере добавления и уточнения деталей. Уровень команд (инструкций) постепенно понижается. Весь процесс заканчивается тогда, когда будет достигнут уровень операторов алгоритмического языка.

Такой метод разработки алгоритмов называется методом пошаговой детализации или проектированием сверху—вниз (от системы команд вы­сокого уровня к системе команд низкого уровня).

Указанный метод разработки алгоритма позволяет получить алгоритм с ясно выраженной структурой, что облегчает понимание и доказательство его правильности.

Рассмотрим примеры реализации основных типов алгоритмов: алгоритмы линейной, разветвляющейся и циклической структуры.

3. . Реализация линейных алгоритмов

Линейными называют алгоритмы, в которых последовательность выполнения инструкций (операторов) совпадает с порядком их записи и не зависит от конкретных значений исходных данных.

К линейным относятся алгоритмы вычислений по определенным формулам. Раздел операторов таких алгоритмов (и соответ­ствующих программ) состоит из трех частей: ввод исходных данных, вы­числения по заданным формулам, вывод требуемых результатов.

Для реализации подобных программ в языке Турбо Паскаль используются опе­ратор присваивания, составной оператор, оператор вызова процедур ввода данных (READ или READLN) и вывода данных (WRITE или WRITELN).

Оператор присваивания

Оператор присваивания — один из основных операторов Турбо Паскаль. Он предназначен для изменения значения переменной или, другими словами, для присваивания переменной нового значения. Общая форма опе­ратора:

<переменная> := <выражение>

Здесь и далее угловыми скобками вы­делены объекты языка, участвующие в определении конструкции.

Выражение в программировании служит для задания действий, которые необходимы для определения нового значения. Например, a + b –1, A*sin( Т ), (x > 0) And (x < 1), ‘Решение’ + ' уравнения’ и т.п.

При выполнении оператора вычисляется указанное справа «выражение», полученное значение присваивается указанной «переменной», старое значение переменной теряется.

Содержание записи операторов присваивания:

А := 27.4 — вещественной переменной А присваивается значение 27.4;

X :=A*sin(T)—вещественной переменной X присваивается значение выражения A*sin(T) при текущих значениях переменных А и Т;

ARR (5) := 0 — пятому элементу массива ARR присваивается значение 0;

F := 'Пример'—символьной переменной F присваивается символь­ное значение «Пример».

В операторе присваивания слева и справа от символа := может фигу­рировать имя одной и той же переменной, например

I := I + 1 — значение целой переменной I увеличивается на 1.

Ввод и вывод данных

Для ввода с клавиатуры используются операторы:

READ(b₁, b₂, ..., b_n);

READLN(b₁, b₂, ..., b_n);

READLN;

где b₁, b₂, ..., b_n — имена переменных, значения которых вводятся.

Оператор READ(b₁, b₂, ..., b_n) осуществляет ввод данных с клавиатуры целого, вещественного, символьного и строкового типов. Типы вводимых данных должны соответ­ствовать типам переменных в списке оператора ввода.

Оператор READLN(b₁, b₂, ..., b_n) осуществляет ввод данных с клавиатуры и после выбора значения последней переменной обеспечивает переход к началу новой строки. При вводе значений целого и действительного типов операторы READ и READLN игнорируют пробелы между значениями.

Оператор READLN обеспечивает пропуск одной строки и переход к началу новой строки.

Для вывода информации используются операторы:

WRITE (b₁, b₂, ..., b_n);

WRITELN(b₁, b₂, ..., b_n);

WRITELN;

где b₁, b₂, ..., b_n — выражения, значения которых выводятся. Обратите внимание на то, что выводить можно только значения целого, вещественного, символьного, логического и строкового типов.

Оператор WRITE(b₁, b₂, ..., b_n) выполняет вывод значений соответствующих выражений на экран, размещая выводимые значения в одной строке.

Оператор WRITELN(b₁, b₂, ..., b_n) выполняет вывод значений выражений на экран и после вывода последнего значения осуществляет переход к началу новой строки.

Оператор WRITELN обеспечивает пе­реход к началу новой строки.

Значения выражений в списке вывода могут принад­лежать к целому, вещественному, символьному или логическому типам. Значения величин вещественного типа выво­дятся в нормализованном виде (мантисса числа с порядком), а цело­го типа — в обычной форме. Операторы вывода допускают использование указания о ширине поля, отводимого под значение.

Общий вид записи операторов для вывода значений целого типа:

WRITE (b:m);

WRITELN(b:m);

а для вывода действительного типа:

WRITE(b:m:n);

WRITELN(b:m:n);

где b — элемент списка вывода; m — поле, отводимое под значе­ние и задаваемое константой или выражением целого типа; n — часть поля, отводимого под дробную часть числа. Например, оператор WRITE (KOL:8,NOM:4) выделяет на строке под значения переменных KOL и NOM соответ­ственно восемь и четыре позиции, а оператор WRITELH(SUM: 10: 5) выделяет под значение SUM десять позиций, из которых пять позиции отводится под дробную часть числа.

Примеры реализации линейного алгоритма

Пример 1.1. Разработать программу вычисления значения функции для произвольных значений ее аргументов:

Y=.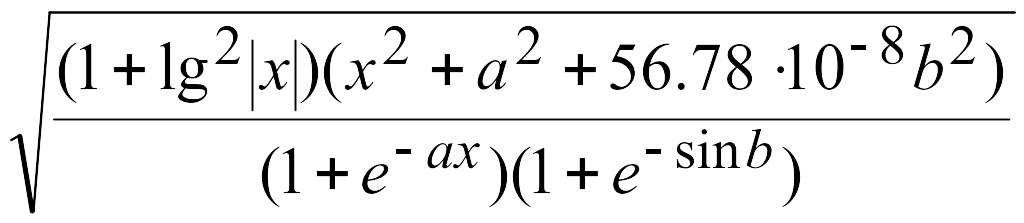

Результаты вычислений вывести с поясняющим текстом.

Решение.

Анализ постановки задачи

Требуется выполнить вычисления по заданной формуле, используя линейный алгоритм решения задачи. Прежде, чем вычислять функцию, необходимо определить значения аргументов а,b,x. После вычислений значения выво­дятся на экран. Другими словами, в алгоритме можно выделить три этапа: ввод исходных данных, вычисления, вывод результатов.

Имена объектов задачи (а следовательно, и объектов программы) фак­тически заданы: аргументы—А, B, X, функция—Y.

Все объекты — переменные вещественного типа.

Ввод исходных данных в задаче — ввод трех переменных. Его можно реализовать одним оператором, например в виде

WRITE(‘Введите аргументы A, B, X: ’);

READLN(A,B,X);

Детализируем этап вывода результатов. Форма вывода в постановке задачи не определена, поэтому принимаем макет печати результатов в виде:

Результаты решения задачи

Аргументы функции: А= **.** В= **.**, X= **.**

Значение функции: Y = *****.**

Здесь и далее символ "*" обозначает любую цифру, а символ "." – десятичную точку, разделяющую целую и дробную части.

Макет вывода результатов определен, а его реализация — последовательность операторов WRITELN - не представляет каких-либо затруднений.

Детализируем этап вычислений. Поскольку задана одна формула, то вычисления можно реализовать одним оператором присваивания. Однако при этом рекомендуется избегать сложных выражений. С этой целью можно использовать разные приемы, например, дополнительные обозна­чения: t=1+lg²|x|, z=x²+a²+56.78 l0^-8 b², v=l+e^-ax ,w=1+е^{-sin b}.

В результате для вычисления функции получим выражение:

Y = SQR-(t -z/v/w).

Этот прием плох тем, что в программе появляются вспомогательные объекты, загромождающие программу.

Более эффективен другой прием, основывающийся на возможности ис­пользовать в операторе присваивания слева и справа от символа присваивания имена одной и той же переменной. В соответствии с этим все вычисления можно представить совокупностью следующих операторов присваивания:

Y:= LN(ABS(X))/LN(10);

Y:=1+Y*Y;

Y:=Y*(X*X+A*A+56.78E-8*B*B);

Y:=Y/(1+EXP(-A*X);

Y:=Y/(1.+EXP(-SIN(B));

Y:=SQR(Y);

Поскольку все этапы решения максимально детализированы, их можно объединить в программу.

Текст программы

PROGRAM Prim11;

{Программа вычисления функции}

{А,В,Х —Аргументы}

{Y—функции}

VAR

A,B,X,Y : REAL;

BEGIN

WRITE(‘Введите аргументы A, B, X: ’);

READLN(A,B,X);

{Этап вычислений}

Y := LN(ABS(X))/LN(10);

Y :=1+Y*Y;

Y:=Y*(X*X+A*A+56.78E-8*B*B);

Y:=Y/(1+EXP(-A*Х));

Y:=Y/(1+EXP(-SIN(B)));

Y:=SQR(Y);

{Этап вывода результатов}

WRITELN(‘Результаты решения задачи');

WRITELN (‘Аргументы функции:');

WRITELN (‘A= ‘,A:5:2,’ B = ‘,В:5:2,’ Х= ‘,Х:5:2);

WRITELN (‘Значение функции — Y= ‘,Y:8:2);

END.

В приведенном тексте программы содержатся поясняющие комментарии. Комментарий в Турбо Паскале – это произвольная последовательность любых символов, обрамленная фигурными скобками. Комментарии не производят никаких алгоритмических действий.

Пример 1.2. Вычислить высоты треугольника со сторонами a, b, c, используя формулы:

,

,

,

где p = (a+b+c)/2.

Решение.

При решении данной задачи для исключения повторений следует вычислять не по приведенным выше формулам непосредственно, а используя промежуточную переменную

,

тогда h_a = t/a, h_b = t/b, h_c = t/c.

Текст программы

PROGRAM PRIM12;

VAR

a, b , c, t, p: REAL;

BEGIN

WRITE(‘Введите длины сторон a, b, c’);

READLN(a, b, c);

p:= (a+b+c)/2;

t:= 2*SQRT(p*(p-a)*(p-b)*(p-c));

WRITELN(‘Высота ha=’,t/a);

WRITELN(‘Высота hb=’,t/b);

WRITELN(‘Высота hc=’,t/c);

END.

Контрольные вопросы

1. Что называется алгоритмом?

2. Для чего необходимы выражения?

3. Какова последовательность действий при выполнении оператора присваивания?

4. Какие имеются средства в языке Турбо Паскаль для управления размещением данных на строке?

5. Как организовать вывод значений, сопровождая выводимое значение наименованием переменной?

6. Как организовать пропуск одной, двух строк при выводе?

Задачи

Эти задачи предназначены для приобретения навыков реализации линейных алгоритмов. Вычислить значения заданных функций.