1.4. Реализация разветвляющихся алгоритмов

Для описания даже простых вычислительных процессов оказывается недостаточно лишь одних линейных алгоритмов. Например, алгоритм вы­числения функции, заданной формулой

уже не является линейным, т. к. в нем должна быть заложена операция выбора одной из формул в зависимости от заданного значения аргумента X. Такого рода алгоритмы называются разветвляющимися, или ветвящими­ся.

В разветвляющихся алгоритмах принцип линейного автоматического перехода от предписания к предписанию (от оператора к оператору) в порядке их естественной записи не является всеобщим, так как возникает потребность выполнения «произвольного» предписания, определяемого не­которыми условиями.

Итак, разветвляющимися называются алгоритмы, в которых по­следовательность выполнения некоторых предписаний определяется выполнением (или невыполнением) определенных условий.

Для реализации разветвлений в Турбо Паскале используются условные опера­торы и оператор выбора. Кроме них может оказаться необходимым оператор перехода.

Условный оператор

Одна из форм условного оператора имеет вид:

IF <условие> THEN <оператор1> ELSE <оператор 2>

Здесь IF (ecлu), THEN (то, тогда), ELSE (иначе) —ключевые слова языка; <условие> — логическое выражение; <оператор1 и оператор2> — один исполняемый оператор.

Смысл условного оператора: если условие при текущих значениях вхо­дящих в него переменных истинно, то выполняется <оператор1> (<опе­ратор2> не выполняется), если же условие ложно, то выполняется <оператор2> (<оператор1> не выполняется). После выполнения <оператора1> или <оператора2> управление передается очередной строке программы, если в <операторах1 и 2> не предусмотрено программ­ное изменение последовательности выполнения строк.

Примеры записи условного оператора:

• для нахождения большего из двух значений:

IF A > В THEN X:=A ELSE Х:=В;

- для нахождения большего из двух значений с фиксацией его имени:

IF A > В THEN

BEGIN

X:=A;

F:=’A’

END

ELSE

BEGIN

X:=B;

F:=’B’

END;

Здесь F переменная символьного типа.

В конструкции условного оператора ветвь «иначе» не обязательна, она может отсутствовать. В этом случае имеет место сокращенная форма услов­ного оператора:

IF <условие> THEN <оператор>

Смысл оператора: если <условие> истинно, то выполняется указанный оператор. Если условие ложно, то оператор не выполняется, управление просто переходит к очередной строке программы.

Очевидно, что один условный оператор в полной форме можно заменить двумя в сокращенной форме; например для нахождения большего из двух значений с фиксацией его имени

IF A > В THEN

BEGIN

X:=A;

F:=’A’

END;

IF A <= В THEN

BEGIN

X:=B;

F:=’B’

END;

В условном операторе после ключевых слов THEN и ELSE можно ис­пользовать другой условный оператор. Получающиеся конструкции называ­ются вложенными условными операторами.

Примеры вложенных услов­ных операторов:

IF Х > 0 THEN

IF Х <= 1 THEN Y:=1 +X

ELSE Y:=X*X;

Здесь возможна неоднозначность исполнения программы с ветвью, сле­дующей за ELSE. Чтобы ее исключить принимается, что ELSE «закрывает» последний «незакрытый» THEN.

Примеры использования условного оператора

Пример 1.3. Вычислить функцию:

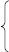1 –e^-x при x < 0,

y = 1 +р при х = 0,

1/(x+p) при 0 < x < 1,

1+psin x при x1.

Решение.

Фрагмент программы

IF X<0 THEN Y:= l + EXP(-X);

IF X=0 THEN Y:=1+P;

IF (X > 0) AND (X < 1) THEN Y:=1/(X+P);

IF X>=1 THEN Y:=1+P*SIN(X);

Пример 1.4. Вычислить значения Y и Z:

Y = ae^-b при ab <1,

b sin² a³ при ab 1,

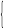
Z = a + cosb при ab < 1,

1/(|b| + e^-a) при ab 1.

Решение.

Фрагмент программы

IF А*В < 1 THEN

BEGIN

Y:=A*EXP(-B);

Z=A+COS(B)

END

ELSE

BEGIN

Y=B*SQR(SIN(A*A*A));

Z=1/(ABS(B)+EXP(-A))

END;

Пример 1.5. Найти наибольшее из трех вещественных чисел (А, В, С) с фиксацией его имени.

Решение.

Фрагмент программы

IF A > В THEN

BEGIN

X:=A;

F:=’A’

END

ELSE

BEGIN

X:=B;

F:=’B’

END;

IF C > X THEN

BEGIN

X:=C;

F:=’C’

END;

Оператор перехода

Оператор перехода (безусловного перехода) используется для изме­нения естественной последовательности выполнения строк программы. Об­щая форма оператора:

GOTO <метка>

Смысл оператора: управление программой передается оператору с указан­ной меткой. Например:

GOTO Metka;

GOTO 200;

Метка назначается пользователем и представляет собой правильный идентификатор или целое число без знака, содержащее не более четырех цифр. Используемые в программе метки должны быть описаны в разделе описания меток.

Операторы перехода при их бессистемном использовании затрудняют чтение программы, делают ее запутанной и трудной для отладки, поэтому говорят, что квалификация программиста обратно пропорциональна количеству операторов перехода в его программах.

С другой стороны, оператор перехода - часто неизбежный оператор при программировании разветвляющихся участков программ.

Учитывая эти два противоречивых высказывания, можно сделать вывод: следует рационально использовать оператор перехода, исключив его ис­пользование, там, где можно использовать другие средства.

Оператор выбора

Оператор выбора (CASE) обеспечивает выполнение одного оператора (простого или сложного) из нескольких возможных. Выбор оператора определяется значением выражения (селектора), которое располагается между ключевыми словами CASE и OF. Значение выражения должно совпадать с константами, стоящими перед операторами. Выражение может принадлежать любому простому типу, кроме вещественного.

Выбор оператора определяется совпадением значения селектора и константы, стоящей перед оператором.

Пример 1.6. Написать программу для вывода дней недели.

PROGRAM Prim16;

VAR

NUMBER : BYTE;

BEGIN

READ (NUMBER);

CASE NUMBER OF

1: WRITELN(‘ПОНЕДЕЛЬНИК’);

2: WRITELN(‘ВТОРНИК’);

3: WRITELN(‘СРЕДА’);

4: WRITELN(‘ЧЕТВЕРГ’);

5: WRITELN(‘ПЯТНИЦА’);

6: WRITELN(‘СУББОТА’);

7: WRITELN(‘ВОСКРЕСЕНЬЕ’);

END

END.

Примеры реализации разветвляющегося алгоритма

Пример 1.7. Разработать программу для вычисления функции

для произвольных значений аргументов.

Решение.

Анализ постановки задачи

На первый взгляд кажется, что решение задачи сводится к линейному алгоритму, т.е. вычислению функции, заданной формулой. Однако это мне­ние ошибочное, так как возможны значения аргументов а и b, обращающие знаменатель дроби в нуль. Следовательно, в таких случаях задача не имеет решения. Поэтому в алгоритме (и программе) необходимо предусмотреть две ветви:

- первая, когда знаменатель обращается в нуль и об этом необходимо вывести сообщение;

- вторая, если знаменатель отличен от нуля, то вычисляется функция и выводятся результаты вычисления.

Если ограничиться выводом простейших сообщений, то решение практически очевидно:

— ввести аргументы функции (А и В);

— вычислить знаменатель;

— если знаменатель равен 0, то выводится “сообщение”;

• если знаменатель не равен 0, то выводится результат.

Все инструкции алгоритма максимально детализированы, поэтому со­ставим текст программы.

Нельзя считать хорошей программу для ЭВМ, если в результате ее исполнения на экран ПК выводится одна малозначащая фраза. Поэтому дополним вывод результатов заголовком, значениями аргументов и расширенным сообщением для первой ветви.

Вариант программы будет иметь вид:

PROGRAM Prim17;

{Программа вычисления функции }

VAR

A,B,Y : REAL;

{А, В — Аргументы }

{Y—Функция}

BEGIN

{Этап ввода исходных данных}

WRITE(‘Введите А=’);

READLN(A);

WRITE(‘Введите B=’);

READLN(B);

{Вычисления и вывод}

Y:=1-A*A+B*B;

IF Y=0 THEN WRITELN(‘Нет решения!’);

IF Y<>0 THEN WRITELN(‘Функция =’, l/Y:7:4);

END.

Пример 1.8. Определить, попадает ли точка с координатами x, y в круг радиуса r с центром в начале координат (уравнение окружности r² = x² + +y²).

Решение.

Вариант программы будет иметь вид:

PROGRAM Prim18;

VAR

x, y, r : REAL;

BEGIN

WRITE(‘Введите радиус окружности R=’);

READLN(R);

WRITE(‘Введите координаты точки X и Y’);

READLN(X, Y);

IF X*X+Y*Y<=R*R

THEN WRITELN(‘Точка лежит внутри круга’)

ELSE WRITELN(‘Точка лежит вне круга’);

END.

Пример 1.9. Составить программу для упорядочивания трех чисел a, b, c по возрастанию таким образом, чтобы имени a соответствовало наименьшее число, имени b – среднее, а имени c – наибольшее.

Решение.

Вариант программы будет иметь вид:

PROGRAM Prim19;

LABEL 10, 20, 30;

VAR A, B, C, H : REAL;

BEGIN

WRITE(‘Введите три числа a, b, c:’);

READ(a,b,c);

IF A<=B THEN GOTO 10

ELSE BEGIN

H:=A;

A:=B;

B:=H

END;

10: IF A<=C THEN GOTO 20

ELSE BEGIN

H:=A;

A:=C;

C:=H

END;

20: IF B<=C THEN GOTO 30

ELSE BEGIN

H:=B;

B:=C;

C:=H

END;

30: WRITELN(‘A=’,A:5:2,’ B=’,B:5:2,’ C=’,C:5:2);

END.

Контрольные вопросы

1. Что такое вычислительный процесс разветвляющейся структуры?

2. Какие управляющие конструкции в Турбо Паскале используются для организации разветвления?

3. Какова последовательность действий при выполнении условного оператора?

4. Какие действия выполняются оператором перехода goto?

5. Почему не рекомендуется использование в программах оператора goto?

6. Какие особенности существуют при написании вложенных операторов If?

7. Какой оператор позволяет выполнить одно из нескольких действий в зависимости от результата вычисления выражения?

Задачи

Эти задания предназначены для при­обретения навыков организации разветвлений.

1. На плоскости расположена окружность радиуса R с цен­тром в начале координат. Ввести заданные координаты точки, определить, лежит ли она на окружности. Решить задачу при R = 2 для точек с координатами (0, 2), (-1.5, 0.7), (1, 1), (3, 0).

Указание. Считать, что точка с координатами х, у лежит на окружности радиуса R, если х² + у² — R² < 10^-3.

2. Вычислить площадь треугольника со сторонами a, b, c по формуле Герона, проверив условие корректности исходных данных (длины всех сторон положительны, сумма длин любых двух сторон больше длины третьей).

3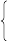 . Для заданных а и b получить

mах(а,b), если a > 0,

C=

min(а,b), если a 0.

4. Для заданных а, b, с вычислить z =max(min(a,b),c).

5. Заданы площади круга R и квадрата S. Определить, поместится ли квадрат в круге. Задачу решить при: 1) R = 70, S =36.74; 2) R=0.86, S= 0.74.

Указание. Для решения задачи выразить диагональ квадрата и диаметр круга через заданные площади фигур. Квадрат поме­стится в круге, если диагональ квадрата не превышает диаметр окружности.

6. Для задачи 5 определить, поместится ли круг в квадрате. Задачу решить при: 1) R = 3.2, S= 3.5; 2) R = 3.2, S = 4; 3) R = 6, S = 9.

В задачах 7 —10 определить значение функции у при заданном аргументе х.

7.

8.

9.

10.

В задачах 11 — 15 определить принадлежность точки (х,y) заданной области. Координаты трех точек задать самостоятельно.

11. у 0 и х² + у² 1.

12. у |x| и у 1- x².

13. у 0, у² 4 - x² и у² 9 - x².

14. х 0, у 0 и x² + у² 4.

15. x 0, y0 и y² 9 - x².

1.5. Реализация циклических алгоритмов

Циклические алгоритмы

Часто при решении задач приходится многократно выполнять одни и те же действия при различных значениях входящих в них величин. Такие многократно повторяющиеся участки вычислительного процесса называются циклами.

Соответственно циклический алгоритм — это алгоритм, содержащий циклы.

Использование циклов позволяет существенно сократить схему алгоритма и длину соответствующей ему программы.

Для организации любого цикла необходимы блоки, выполняющие следующие функции:

1. Задание начального значения переменной, изменяющейся в цикле.

2. Изменение переменной перед каждым новым повторением цикла.

3. Проверку условия окончания цикла и выход из него, если цикл закончен.

4. Переход к началу цикла, если цикл не закончен.

Отметим, что возможен «досрочный» выход из цикла с помощью услов­ного оператора и оператора перехода, а также процедур Break или Exit.

Различают два типа циклов: циклы с известным числом повторений (арифметические) и циклы с неизвестным числом повторений (итерационные). Подчеркнем, что число по­вторений определяется на момент разработки алгоритма.

Цикл, содержащий внутри себя один или несколько других циклов, называется вложенным. Цикл, охватывающий другие циклы, называется внешним, а остальные - внутренними. Правила организации для внешних и внутренних циклов такие же, как и для простого цикла. Параметры этих циклов изменяются не одновременно: при одном значении параметра внешнего цикла параметр внутреннего цикла принимает по очереди все свои значения. В качестве параметров для этих циклов должны использоваться переменные с разными именами.

Реализация циклических алгоритмов

Для реализации циклов в программах на языке Турбо Паскаль можно использо­вать условные операторы в сочетании с оператором перехода, но наиболь­ший эффект дают специальные операторы— операторы циклов.

Прежде всего рассмотрим циклы с заданным (известным) числом по­вторений.

Цикл с известным числом повторений

Цикл с известным числом повторений в Турбо Паскаль называется также цик­лом с параметром. Общая форма конструкции, образующей цикл, имеет вид:

- при увеличении значения параметра

FOR <переменная> = Выр.1 ТО Выр.2 <оператор>

• при уменьшении значения параметра

FOR <переменная> = Выр.1 DOWNТО Выр.2 <оператор>

Здесь FOR (для), ТО (до), DOWNТО — ключе­вые слова языка Турбо Паскаль. <Переменная> называется параметром цикла, или управляющей переменной цикла. В качестве нее можно использовать любую переменную порядкового типа.

Выр.1, Выр.2 — выражения, определяющие соответственно начальное и конечное значения параметра цикла. Они могут быть записаны константами или выражениями, совпадающими по типу с параметром цикла. Выр.1, Выр.2 вычисляются до входа в тело цикла.

Первая строка конструкции (оператор FOR) обычно называется заго­ловком цикла. Оператор, следующий за ним, образует тело цикла. Это может быть любой исполнимый оператор языка, в том числе и составной .

Примеры реализации циклического алгоритма

Пример 1.10. Разработать программу для вычисления суммы К членов ряда, определяемых общей формулой

C_i = (-1)ⁱ⁺¹ для аргумента х > 0.

Решение.

Анализ постановки задачи

В формуле для членов ряда символом «!» обозначена функция, называ­емая факториалом и определяемая в виде:

К!=1∙2∙3∙...∙К.

Исходными данными для решения задачи, очевидно, являются число членов ряда K и значение аргумента Х.