Файл: Электронное пособие Scilab.pdf

106 

Тема 2.4. Технология решения обыкновенных  

дифференциальных уравнений 

2.4.1. Численное решение обыкновенных дифференциальных уравнений 

2.4.2.  Лабораторная работа  
2.4.3. Контрольные вопросы по теме

2.4.1.  

Численное решение решения обыкновенных  

дифференциальных уравнений 

Представим  обыкновенное  дифференциальное  уравнение  (ОДУ) 

первого порядка в виде, разрешенном относительно производной

)

,

( y

x

f

y 



,и 

пусть 

y

x

y



)

(

0

– начальные условия его решения. 

Тогда  решением  ОДУ  является  функция 

)

( x

y





,  которая  будучи 

подставленной  в  исходное  уравнение,  обратит  его  в  тождество,  и 
одновременно  будут  выполняться  начальные  условия.  Эта  задача  в 
математике называется задачей Коши. 

Задача  Коши  при  решении  ОДУ  n-го  порядка 

)

,...

,

,

(

)

1

(

)

(







n

n

y

y

y

x

f

y

формулируется аналогично, при этом начальными условиями должны быть: 

.

)

(

...

,

)

(

,

)

(

)

1

(

0

0

)

1

(

0

0

0

0















n

n

y

x

y

y

x

y

y

x

y

При  решении  Оду  n-го  порядка 

уравнение путем выполнения ряда обозначений 

)

...

,

,

(

1

2

2

1

1

















n

n

y

y

y

y

y

y

представляется в виде системы дифференциальных уравнений: 



































).

,...,

,

,

(

;

..

..........

;

;

1

1

)

(

1

2

1

1

n

n

n

n

y

y

y

x

f

y

y

y

y

y

y

y

 
Результатом  решения  ОДУ  численными  методами  является  таблица 

значенийy  =  (x)  на  некотором  множестве  значений  аргументах.  Поэтому 
при  постановке  задачи  численного  решения  ОДУ  наряду  с  начальными 
условиями  x

0

,  y

0

необходимо  задать  область  решения  –  отрезок  [a;b]  и  шаг 

изменения аргумента h (шаг интегрирования). 

Для  получения  численного  решения  ОДУ  используются  методы 

Рунге-Кутты.  Методы  различаются  порядком.  Чем  выше  порядок  метода, 
тем точнее решение, полученное при равном шаге интегрирования.  
 

Для  решения  дифференциальных  уравнений  и  систем  в  Sciab 

предусмотрена функция: 
 

[y,w,iw]=ode([type],y0,t0,t [,rtol [,atol]],f [,jac] [,w,iw]), 

107 

для которой, обязательными входными параметрами являются:  

y0 -  вектор начальных условий;  
t0  - начальная точка интервала интегрирования; 
 t  - координаты узлов сетки, в которых происходит поиск решения;  
f      -  внешняя  функция,  определяющая  правую  часть  уравнения  или 

системы уравнений; 

y -  вектор решений. 

 
Таким 

образом, 

для 

того 

чтобы 

решить 

обыкновенное 

дифференциальное уравнение необходимо вызвать функцию y=ode(y0,t0,t,f). 

 
Рассмотрим необязательные параметры функции ode: 
type–  параметр,  с  помощью  которого  можно  выбрать  метод  решения 

или  тип  решаемой  задачи,  указав  одну  из  строк:  adams  -  применяют  при 
решении  дифференциальных  уравнений  или  систем  методом  прогноза  - 
коррекции Адамса; 

stiff - указывают при решении жестких задач; 
rk  -  используют  при  решении  дифференциальных  уравнений  или 

систем методом Рунге-Кутты четвертого порядка; 

rkf  -  указывают  при  выборе  пятиэтапного  метода  Рунге-Кутты 

четвертого порядка;  

fix - тот же метод Рунге-Кутты, но с фиксированным шагом; 
rtol,  atol  -  относительная  и  абсолютная  погрешности  вычислений, 

вектор,  размерность  которого  совпадает  с  размерностью  вектора  y,  по 
умолчанию rtol=0.00001, atol=0.0000001 (при использовании параметров rkf 
и fix - rtol=0.001, atol=0.0001); 

jac-    матрица,    представляющая    собой    якобиан    правой    части  

жесткой    системы  дифференциальных  уравнений,  задают  матрицу  в  виде 
внешней функции вида J=jak(t,y);  

w,  iw  -  векторы,  предназначенные  для  сохранения  информации  о  

параметрах  интегрирования,  которые  применяют  для  того,  чтобы 
последующие вычисления выполнялись с теми же параметрами. 

Рассмотрим  использование  функции  ode()  на  примере  решения 

следующей задачи. 

 
Пример 2.4.1-1

. 

Найти решение ОДУ 

)

sin(

y

x

y









на отрезке [0;5] 

cшагом 0.5 при начальных условиях

;

5

.

1

)

0

(



y

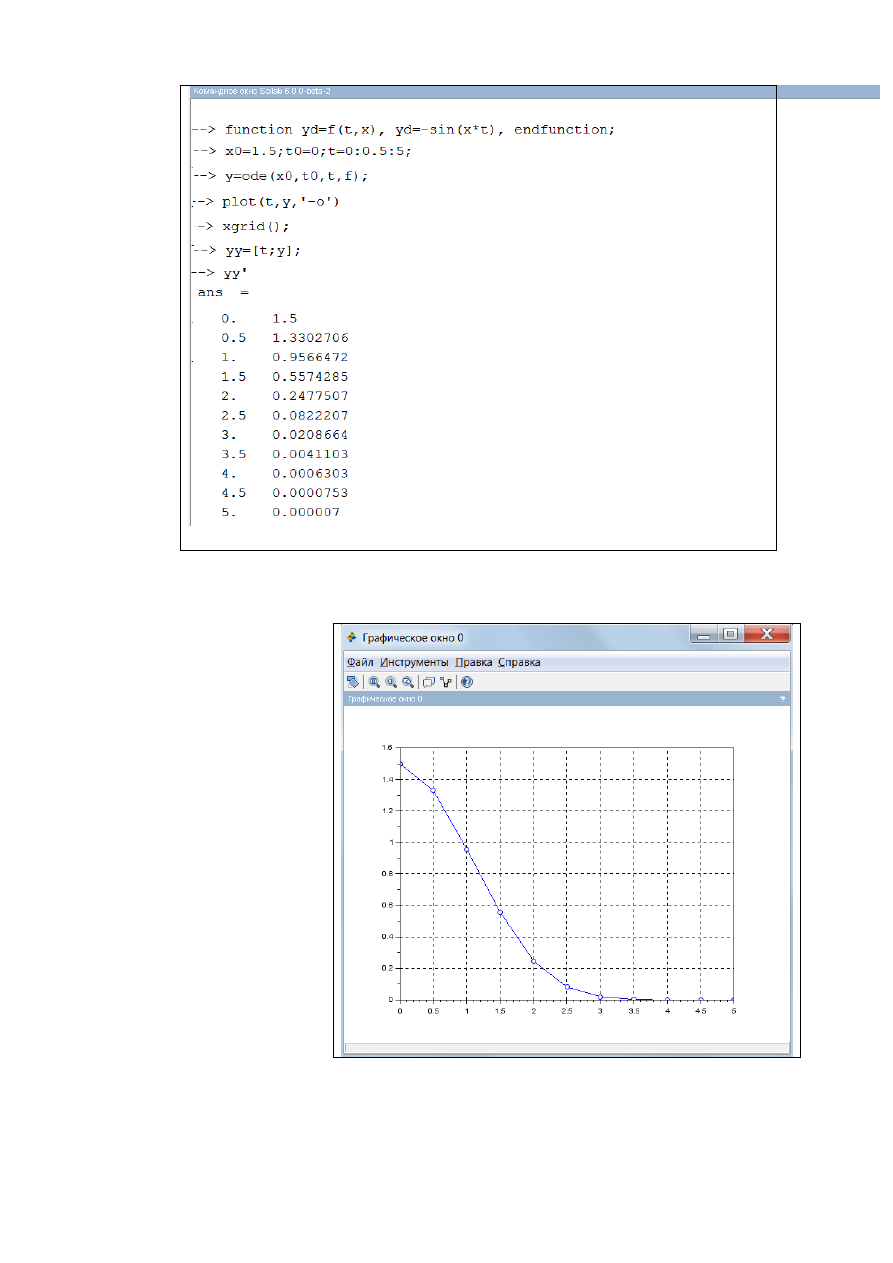
108 

Рис. 2.4.1-1. Решение ОДУ с использованием функции ode() 

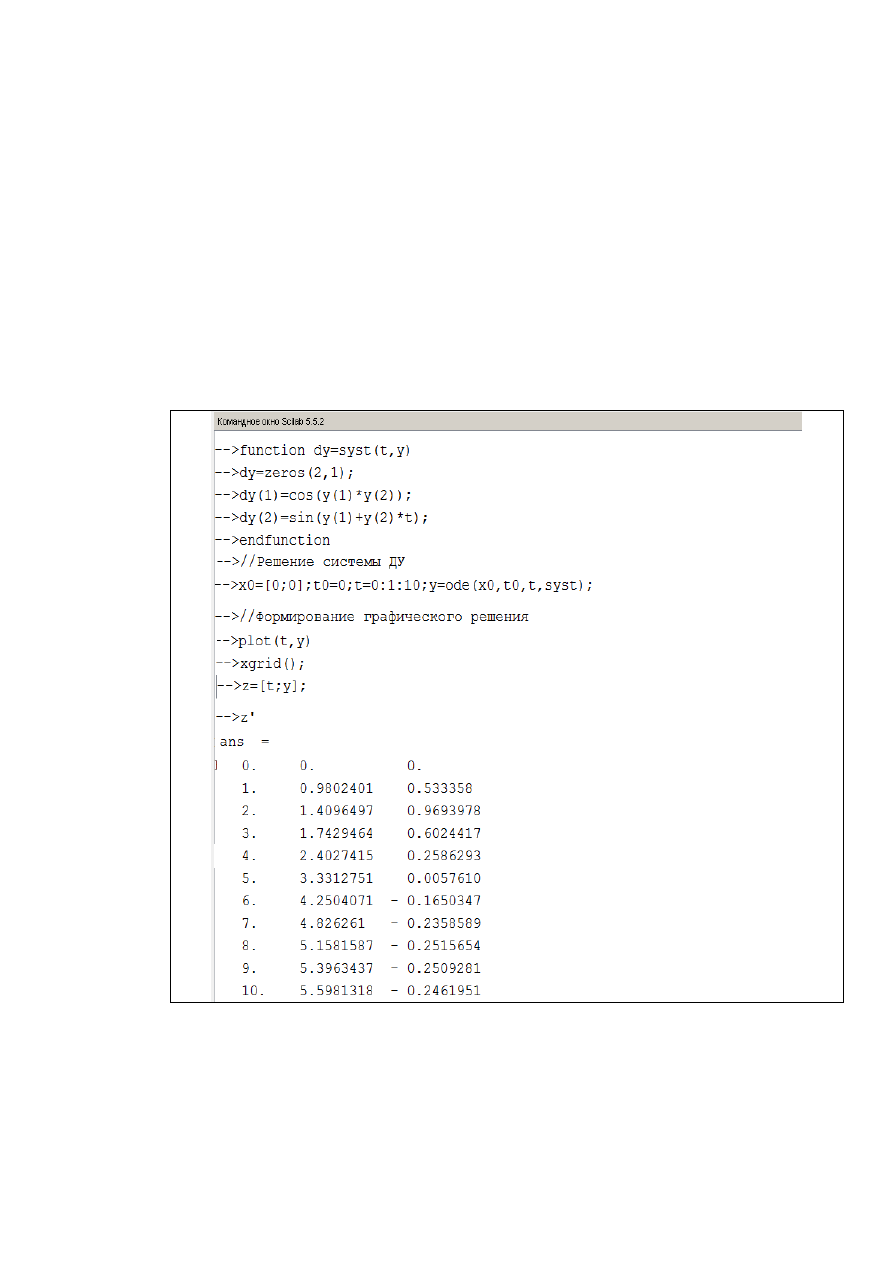
Рис. 2.4.1-2.  Графическое решение ОДУ 

109 

Пример 2.4.1-2

.

Решить систему ОДУ

.

0

)

0

(

;

0

)

0

(

;

)

sin(

);

cos(





















y

x

ty

x

y

xy

x

Решение  системы  ОДУ  в  Scilab  начинается  с  функции,  описывающей 

систему (рис.2.4.1-3). 

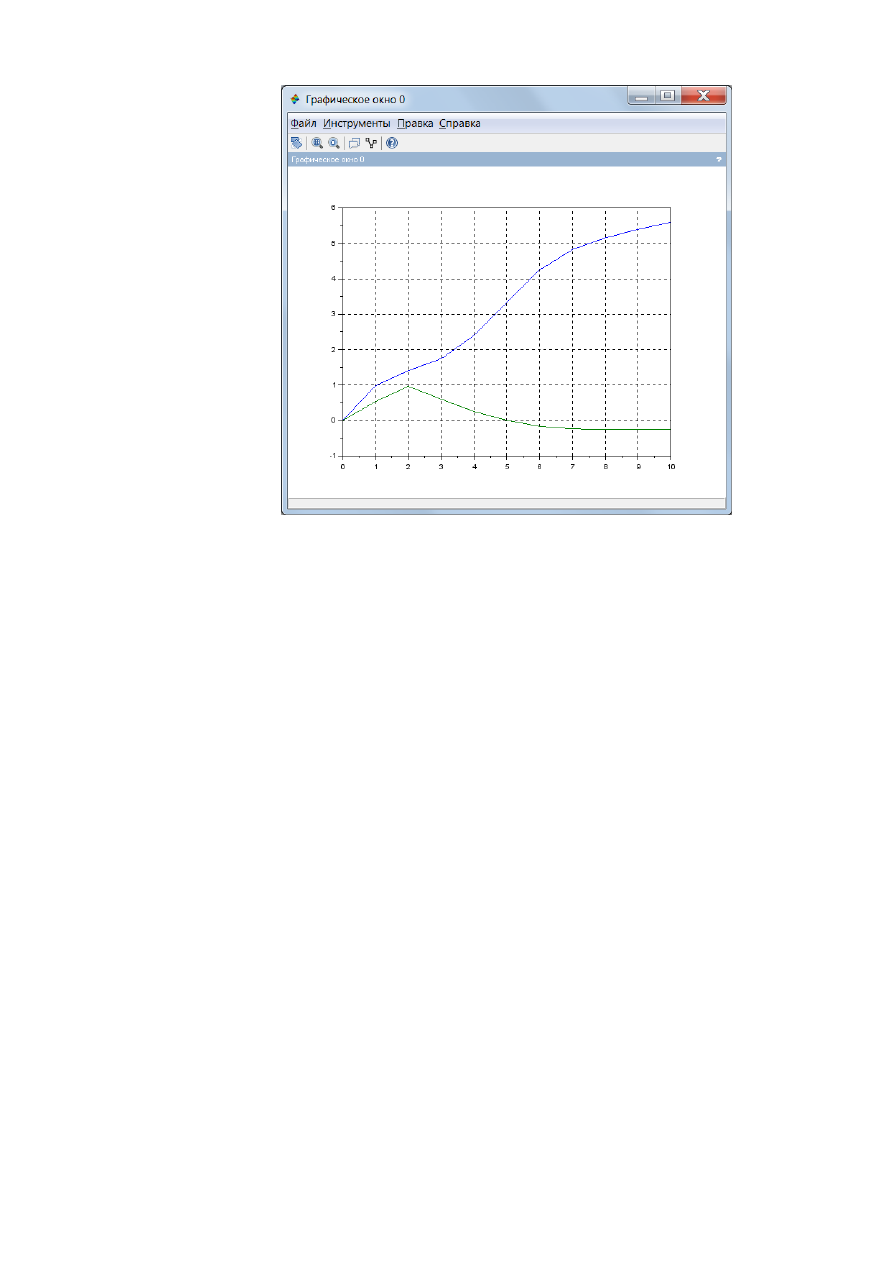
Для  решения  дифференциального  уравнения  (системы  уравнений) 

используем команды, где решение системы ОДУ записывается в переменную 
y.  При  этом  элемент  y(1)  содержит  значение  функцииy(x),  а  y(2)  значение 
производной y'(x). Команда plot(x, y)  строит график функции решения ОДУ 
и ее производной (рис. 2.4.1-6). 

Рис.2.4.1-4. Решение системы ОДУ  

110 

Рис.2.4.1-5. Графики функций решения ОДУ и производной