15 марта 1919 г. был подписан декрет о создании Государственной картографо-геодезической службы – Высшего геодезического управления, реорганизованного впоследствии в Главное управление геодезии и картографии (ГУГК) при СМ СССР.

В конце 1920-х гг. Ф. Н. Красовский разработал программу развития ГГС. Созданная по этой программе единая астрономо-геодезическая сеть не имела аналогов в мировой практике по стройности построения и точности. В 1940 г. под руководством Ф. Н. Красовского и А. А. Изотова были вычислены новые размеры Земли, принятые для геодезических и картографических работ на территории СССР. Таким образом, была создана единая государственная опорная геодезическая сеть, частью которой является существующая государственная геодезическая сеть Республики Беларусь.

Начало геодезического образования в Беларуси относится к 1859 г., когда в Горе-Горецком земледельческом институте были открыты землемерно–таксаторские классы. В настоящее время подготовку специалистов осуществляют Борисовский политехникум – техников-топографов и Полоцкий политехнический университет, готовящий инженеров-геодезистов.

В настоящее время на всю территорию Республики Беларусь созданы топографические карты масштаба 1:10 000, а на территорию городов и городских поселков – топографические планы масштабов 1:5000 и 1:2000, в том числе, на застроенные территории городов – топопланы масштабов 1:1000 и 1: 500.

Все топографо-геодезические работы государственного значения выполняются производственными подразделениями «Белгеодезия», «Белаэрокосмогеодезия» и другими, входящими в структуру Комитета по земельным ресурсам, геодезии и картографии при Совете Министров Республики Беларусь.

1.3. Единицы мер в топографии и геодезии

Совокупность единиц физических величин, принятых в государстве для измерений называется системой мер.

При производстве геодезических измерений единицей угла служит градус, равный 1/360 части окружности или 1/90 части прямого угла (1º = 60΄, 1΄= 60΄΄). Пример: 11º 07´ 56´´.

Наряду с градусной системой мер в некоторых странах употребляется десятичная или децимальная система, в которой прямой угол делят на 100 частей, называемых градами. Град делится на 100 минут или сантиград, а минута – на 100 секунд. Пример: 46^g 68^s 98^ss или 46,6898 ^g.

Значение угла может быть выражено в радианной мере. Радиан ρ – центральный угол, соответствующий длине дуге окружности, равной ее радиусу. Величина радиана – ρ = 57º 17΄ 44,8΄΄ или ρ ≈ 57,3; ρ΄ ≈ 3438; ρ΄΄ ≈ 206 265, где ρ, ρ΄, ρ΄΄ – число градусов, минут, секунд в радиане.

Единица длины – метр (м). За метр принята длина “архивного метра” платинового жезла, хранящегося в международном бюро мер и весов во Франции. Длина жезла была принята равной одной десятимиллионной части четверти Парижского меридиана. В 1889 г. была изготовлена 31 копия «архивного метра», две из которых были переданы в Россию. Для создания надежно воспроизводимого эталона метра в 1960 г. было решено выражать его через длину световых волн. В 1983 г. принято новое определение метра, согласно которому метр равен расстоянию, проходящему в вакууме плоской электромагнитной волной за 1/299 792 458 доли секунды. Кратные единицы метра –1 км = 1000 м; 1 дм = 0,1 м; 1 см = 0,01 м и 1мм = 0,001 м.

Единица площади – квадратный метр (м²). Кратные единицы –  1км² = 1 000 000 м² ; 1 см² = 0,0001 м² ; 10 000 м² = 1 га; 1 км² = 100 га.

Единица времени – секунда (s). Секунда равна 9 192 631 770 периодам излучения, соответствующего перехода между двумя сверхтонкими уровнями основного состояния атома Цезия-133. 1^m(мин) = 60^s; 1^h (час) = 3600 ^s.

Единица температуры – градус по шкале Цельсия (С).

Единицей массы служит килограмм (кг). Копия представляет платиново-иридиевую гирю – цилиндр диаметром и высотой 39 мм.

Единица силы – ньютон (Н). 1Н равен силе, сообщающей телу массой 1кг ускорение 1 м/сек² в направлении действия силы.

Единицей измерения давления служит паскаль (Па). Паскаль равен давлению, вызываемому силой 1Н равномерно распределенной по нормальной к ней поверхности площадью 1м². 1 Па = 9,87× 10 ^–6 атм. или 7,60 × 10^–3мм.рт.ст. Давление, равное 1013 г Па на уровне моря на широте 45 принято считать нормальным.

2. ОБЩИЕ СВЕДЕНИЯ

2.1. Форма и размеры Земли

Физическая поверхность Земли представляет собой сочетание бесконечно большого числа неровностей. Она состоит из океанов, морей и материков с островами. Поверхность океанов в их спокойном состоянии ровная, а суша, составляющая только 29 % от общей площади Земли, представляет собой сложные сочетания гор, возвышенностей, равнин и низменностей. Поэтому поверхность Земли не имеет математического выражения, хотя для решения задач науки и практики требуется знать пространственное положение ее точек. Устанавливать их удобно относительно вспомогательной поверхности, близкой к реальной (физической) поверхности Земли. Такую поверхность называют поверхностью относимости, за которую принимается основная уровенная поверхность Земли, в каждой точке которой нормаль совпадает с направлением отвесной линии (с направлением силы тяжести). Это поверхность воды океанов и открытых морей, находящаяся в спокойном состоянии и мысленно продолженная под материками так, что к ней отвесные линии перпендикулярны во всех точках на Земле. Выбор поверхности воды океанов и морей за уровенную поверхность Земли, объясняется тем, что поверхность открытых водных пространств занимает 71 % общей площади Земли.

В 1873 г. немецкий физик И. Б. Листинг назвал эту поверхность поверхностью геоида. Однако и фигура геоида сложна и строго неопределима, поскольку зависит от малоизученного распределения масс внутри Земли. Поэтому поверхность геоида не соответствует поверхности ни одной правильной математической фигуры, что не позволяет проводить расчеты, связанные с обработкой геодезических измерений на земной поверхности.

По предложению ученого М. С. Молоденского вместо геоида в качестве промежуточной поверхности относимости используется квазигеоид, выполняющий роль «уровня моря». Положение его поверхности рассчитывается на основе гравиметрических измерений (см. 2.2). Поверхности квазигеоида и геоида совпадают с поверхностью Мирового океана и различаются по высоте на суше не более чем на 2,5 м.

Геоид и квазигеоид по форме близко подходят к правильной математической фигуре – эллипсоиду вращения. Поэтому в качестве основной уровенной поверхности при обработке геодезических измерений, выполняемых на земной поверхности принята поверхность эллипсоида вращения, представляющего собой фигуру, полученную в результате вращения эллипса вокруг его малой оси (земной) эллипсоид.

Угол между отвесной линией pq к поверхности геоида в данной точке и нормалью mn к поверхности эллипсоида называется уклонением отвесной линии  (рис. 2.1). В среднем, значение  составляет 3–4″, а в местах аномалий достигает десятков секунд.

Рис. 2.1

Земной эллипсоид характеризуется следующими основными элементами (рис. 2.2.): малой полуосью (полярный радиус) , которая совпадает с осью вращения Земли; большой полуосью (экваториальный радиус) , которая перпендикулярна оси вращения Земли и полярным сжатием .

Э лементы земного эллипсоида, рассчитан–ные Деламбром (1800), Бесселем (1841), Хейфордом (1909) и другими учеными неоди–наковы, так как вычислены по геодезическим измерениям разных по протяженности дуг ме–ридианов и параллелей.

З

Рис. 2.2

На территории СССР пользовались эллипсоидом Ф. В. Бесселя до 1946 г. Однако этот эллипсоид был рассчитан в основном по данным Западной Европы. На Дальнем Востоке его поверхность сильно уклонялась от поверхности Земли.

Более точные результаты размеров земного эллипсоида были получены в 1940 г. Ф. Н. Красовским и А. А. Изотовым по результатам астрономо-геодезических работ, выполненных на территории СССР, Западной Европы и США. Размеры земного эллипсоида, получившего название «референц-эллипсоида Красовского», были приняты для геодезических и картографических работ на всей территории СССР. Отклонения поверхности референц-эллипсоида Красовского от поверхности геоида не превышают 150 м. Точкой ориентирования референц-эллипсоида Красовского является центр круглого зала Пулковской обсерватории, широта В₀ и долгота L₀ которого определены из астрономических наблюдений и приняты исходными, а поверхность эллипсоида совмещена со средним уровнем воды в Финском заливе и отмечена на Кронштадском футштоке.

В настоящее время основные геометрические параметры общеземного эллипсоида определяются более точными методами с использованием искусственных спутников Земли. Для сравнения в табл. 2.1 приведены размеры земного эллипсоида, определенные Бесселем, Красовским и в глобальной геоцентрической системе координат WGS – 84 (World Geodetic System 1984).

Таблица 2.1.

Размеры земного эллипсоида

При картографических работах (составление карт мелких масштабов) Землю достаточно принимать за шар, объем которого равен объему земного сфероида. Исходя из размеров эллипсоида Красовского R = 6 371 110 м.

2.2. Методы определения формы и размеров Земли

Астрономо-геодезический метод. Определение формы и размеров Земли при помощи этого метода основано на использовании градусных измерений, суть которых сводится к определению линейной величины дуг меридианов и параллелей на разных широтах.

Первое известное в истории определение длины земного меридиана, выполненное в античное время в Египте принадлежит Эратосфену. По его определениям длина меридианной окружности, равнялась 39 500 км, то есть очень близко к действительной величине меридиана 40 009 км. Ряд допущений, сделанных Эратосфеном, и несовершенный метод линейных измерений (расстояние определялось по длине караванного пути, измеренное в египетских стадиях (1 стадия может быть приравнена к 157,5 м) привели к приближенным результатам. Однако значение выполненных работ заключается в том, что Эратосфен впервые применил геодезический метод определения размеров Земли и получил довольно удовлетворительные для того времени результаты.

Высокая точность измерения значительных по протяженности расстояний обеспечивается методом триангуляции, который был разработан в 1615 г. голландским ученым В. Снеллиусом. Триангуляция (от лат. triangulum – треугольник) – способ определения положения опорных геодезических пунктов А, В, С,… на местности путем построения сети примыкающих друг к другу треугольников, в которых измеряются все углы, а с помощью базиса аb определяется длина выходной стороны АВ в их ряду, длины же других сторон вычисляют по координатам этих пунктов (рис. 2.3).

Рис. 2.3

Триангуляция являлась основным способом создания опорной геодезической сети и градусных измерений до развития и становления космического метода. Триангуляционные работы по определению длины дуг меридианов и параллелей проводились учеными разных стран (см. п. 1.2 и 2.1).

Геофизический (гравиметрический) метод. Геофизика – это наука, изучающая физические свойства Земли в целом и процессы, происходя­щие в ее геосферах. Этот метод основан на измерении величин, характе­ризующих земное поле силы тяжести, и их распределение на по­верхности Земли. Измерения потенциала силы тяжести, выполняемые на поверхности Земли, позволяют вычислять сжатие Земли с большей точностью, чем астрономо-геодезическим методом.

Преимуществом этого метода является то, что его можно использо­вать на акваториях морей и океанов, где возможности астрономо-геодезического метода ограничены. С именем французского ученого А. Клеро (1713–1765) связано применение гравиметрического метода. В 1743 г. предполагая, что Земля состоит из сфероидальных слоев с общим центром, плотность которых возрастает к центру, он получил формулу для вычисления ускорения силы тяжести в любой точке Земли:

,

где g_φ ; g_э; g_n– ускорение силы тяжести, соответственно, на определяемой широте φ, на экваторе и на полюсе. Если в имеющуюся формулу подставить числовые значения g_э и g_n , полученные путем измерений, то формула примет вид: g _φ = 978, 030 (1+ 0,005302 sin² φ).

Развитие космического метода относится к периоду освоения космического пространства с помощью ИСЗ. Этот метод основан на наблюдениях за ИСЗ и определении координат в заданный момент времени. Выявление отклонений реальных орбит ИСЗ от предвычисленных, вызванных неравномерным распределением масс в земной коре, позволяет уточнить представление о гравитационном поле Земли, а, следовательно, о ее форме и размерах (см. п. 7.5).

2.3. Методы проецирования земной поверхности

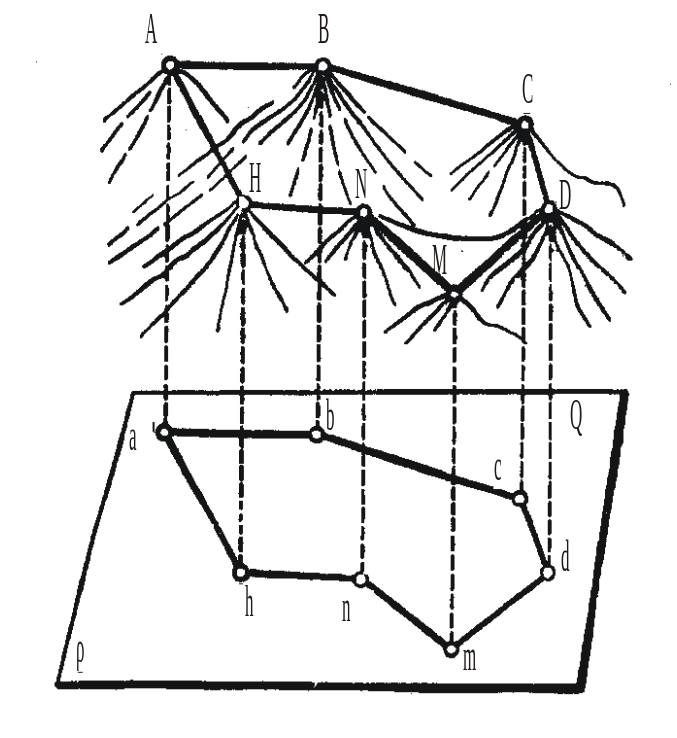
Для составления топографических карт и планов точки земной поверхности проецируют на поверхность референц-эллипсоида или на плоскость. Проецирование на поверхность референц-эллипсоида выполняется вдоль отвесных линий. Четырехугольник аbcd, полученный проецированием на сферическую поверхность эллипсоида, называют горизонтальной проекцией четырехугольника ABCD местности (рис. 2.4).

При проецировании небольших по площади участков местности, основную уровенную поверхность можно принимать за плоскость. В таком случае отвесные линии можно считать параллельными между собой и горизонтальная проекция практически преобразуется в ортогональную. Согласно рис. 2.5 отрезки ab, bc, cd,…являются ортогональными проекциями соответствующих линий AB, BC, CD,…, углы abc, bcd,…– ортогональными проекциями соответствующих углов ABC, BCD,…, а плоский многоугольник abcd – ортогональной проекцией пространственного многоугольника ABCD. Положение точек и линий местности АВ,ВС,… в ортогональной проекции определяется длинами горизонтальных проложений ab,bc,…и горизонтальными углами между ними.

Длина ортогональной проекции линии местности MN на горизон-тальную плоскость p называется горизонтальным проложением S этой линии (рис. 2.6) и вычисляется из прямоугольного треугольника MNC по формуле S = L×cos ν.

Угол ν между линией местности MN и ее ортогональной проекцией на горизонтальную плоскость S = mn, измеряют непосредственно и называют углом наклона линии. Ортогональные проекции линий на плоскость при ν ≠ 0 всегда меньше соответствующих им отрезков на физической поверхности Земли.

2.4. Размеры участков земной поверхности,

принимаемые за плоскость

Р ассмотрим, для каких по размерам участков местности можно применять ортогональное проецирование, т. е. при которых кривизна Земли может не учитываться в процессе создания карты или плана. На рис. 2.7 изображена часть поверхности Земли в виде дуги BCD радиуса R и ее проекция PQ на плоскость PCQ, где PC = CQ.

Д

Рис. 2.7