Определим разность между длиной касательной S и длиной дуги S₁. Выразим угол a в радианах, тогда согласно рис. 2.7 получим, что S = R × tga, а S₁ = R×a. Откуда следует, что

DS = R(tga -a). (2.1)

Центральный угол a по своей величине незначителен. Поэтому при разложении tga в убывающий ряд можно ограничиться вторым членом ряда и пренебречь последующими из-за их незначительности. Тогда . Подставим это значение в формулу 2.1. В результате получим, что

. (2.2)

Из формулы S₁=R×a получим, что и заменим a в форму­ле 2.2. Окончательно найдем, что

. (2.3)

Из рис. 2.7 видно, что точка D находится на уровенной поверхности и ее высота равна нулю. Определим величину отрезка, характеризующего отклонение точки Q от уровенной поверхности. Для этого рассмотрим прямоугольный треугольник OCQ, откуда (R + h)² = S² + R². Упростив данное равенство, имеем . Ввиду малого значения h в сравнении с 2R окончательно получим, что

. (2.4)

Сравнивая формулы 2.3 и 2.4 видно, что значение h существенно больше DS. Если условно принять радиус Земли постоянным, то можно вычислить расхождения DS между длинами дуг на уровенной поверхности и их проекциями на плоскость, а также отклонения высот точек h от их положения на поверхности сферы из-за кривизны Земли (табл. 2.2).

Таблица 2.2

Значение величины DS возрастает незначительно. При дуге 11 км DS составляет лишь 1:1 000 000 ее длины. Относительная погрешность измерения расстояний современными приборами составляет порядка 1:1 000 000. Поэтому принято считать, что участок радиусом 11 км можно принимать за плоскость, а при определении превышений между точками местности необходимо вводить поправку h.

2.5. Cистемы координат, применяемые в топографии
и геодезии

Координаты – это величины, определяющие положение любой точки на поверхности или в пространстве в принятой системе координат. Система координат устанавливает начальные (исходные) точки, линии или плоскости для отсчета необходимых величин – начало отсчета координат и единицы их исчисления. В топографии и геодезии наиболь­шее применение получили системы географических, прямоугольных, полярных и биполярных координат.

Г

Рис. 2.8.

Географические координаты – это угловые величины: долгота l и широта j.

Географической долготой l называется двугранный угол, заключенный между плоскостью данного меридиана (проходящего через точку В) и плоскостью начального меридиана. За начальный (нулевой) меридиан принят меридиан, проходящий через центр главного зала Гринвичской обсерватории в пределах г. Лондона. Для точки В долгота определяется углом l = WCD. Счет долгот ведут от начального меридиана в обе стороны – на восток и на запад. В связи с этим различают западные и восточные долготы, которые изменяются от 0° до 180°.

Географической широтой j называется угол, составленный плоскостью экватора и отвесной линией, проходящей через данную точку. Если Землю принимать за шар, то для точки В (рис. 2.8) широта j определяется углом DCB. Широты, отсчитываемые от экватора к северу, называются северными, а к югу – южными, они изменяются от 0° на экваторе до 90° на полюсах.

Географические координаты могут быть получены на основании астрономических наблюдений или геодезических измерений. В первом случае их называют астрономическими, а во втором – геодезическими (L – долгота, B – широта). При астрономических наблюдениях проецирование точек на поверхность относимости осуществляется отвесными линиями, при геодезических измерениях – нормалями. Поэтому величины астрономических и геодезических координат отличаются на величину уклонения отвесной линии.

Использование разными государствами различных референц-эллип­соидов приводит к различиям координат одних и тех же пунктов, вычисленных относительно разных исходных поверхностей. Практически это выражается в общем смещении картографического изображения относительно меридианов и параллелей на картах крупного и среднего масштабов.

П рямоугольными координатами (рис. 2.9)

называются линейные величины – абсцисса и ордината, определяющие положение точки на плоскости относительно исходных направлений.

В

Рис. 2.9

Прямая ХХ (ось абсцисс) совмещается с направлением меридиана, проходящего через начало координат, или с направлением, параллельным некоторому меридиану. Прямая YY (ось ординат) проходит через точку О перпендикулярную оси абсцисс. В такой системе положение точки на плоскости определяется кратчайшим расстоянием до нее от осей координат. Положение точки А определяется длиной перпендикуляров X_а и Y_а. Отрезок X_а называется абсциссой точки А, а Y_а – ординатой этой точки. Прямоугольные координаты обычно выражаются в метрах. Осями абсцисс и ординат участок местности в точке О делится на четыре четверти (рис. 2.9). Название четвертей определяется принятыми обозначениями стран света. Четверти нумеруются по направлению хода часовой стрелки: I – СВ; II – ЮВ; III – ЮЗ; IV – СЗ.

В табл. 2.3 показаны знаки абсцисс Х и ординат Y для точек, находящихся в разных четвертях и даны их названия.

Таблица 2.3

Абсциссы точек, расположенные вверх от начала координат считаются положительными, а вниз от нее – отрицательными, ординаты точек, расположенные вправо – положительными, влево – отрицательными. Система плоских прямоугольных координат применяется на ограниченных участках земной поверхности, которые могут быть приняты за плоские.

Рис. 2.10

Система биполярных координат (рис. 2.11) представляет собой два выбранных неподвижных полюса О₁ и О₂ , соединенные прямой – полярной осью. Данная система координат позволяет определить положение точки М относительно полярной оси на плоскости при помощи двух углов b₁ и b₂, двух радиусов-векторов r₁ и r₂ или их комбинаций. Если известны прямоугольные координаты точек О₁ и О₂ , то положение точки М можно вычислить аналитическим способом (см. 7.4).

.

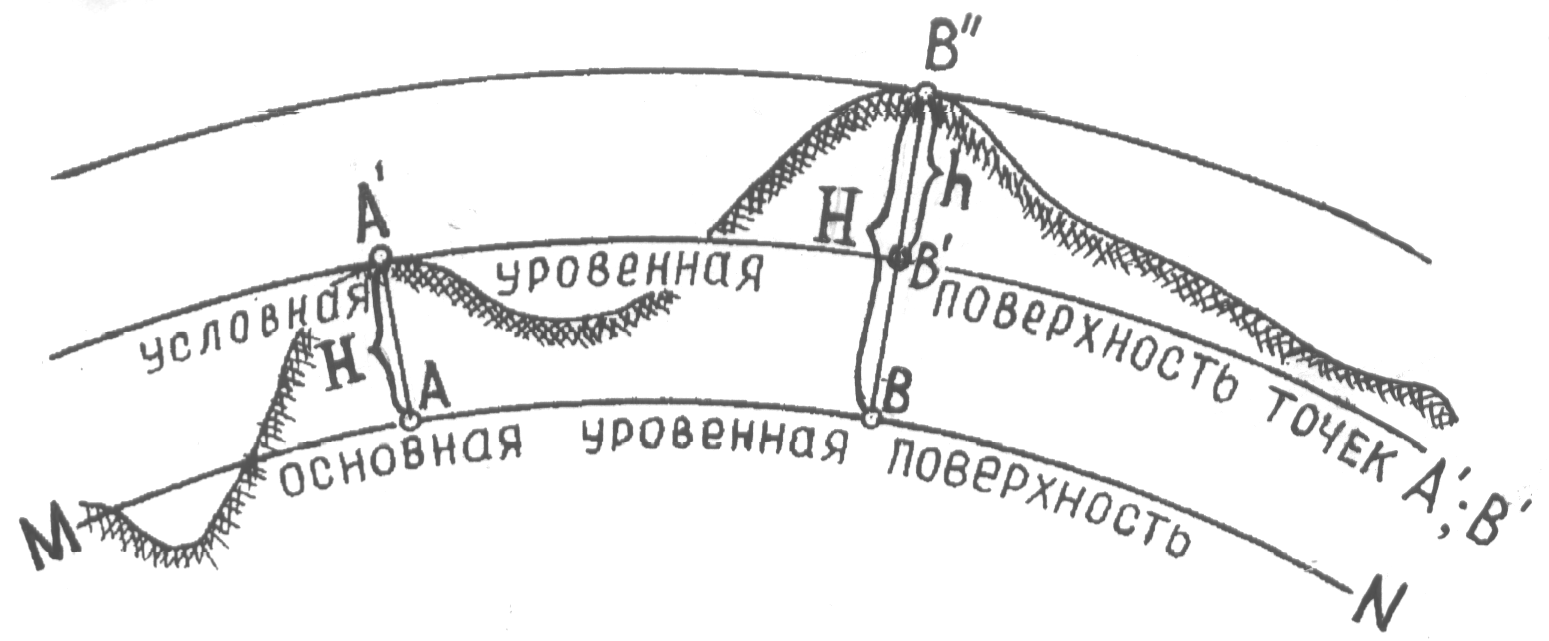
Высоты точек земной поверхности. Для определения положения точек физической поверхности Земли недостаточно знать только плановые координаты X, Y или l, j, необходима третья координата – высота точки Н. Высотой точки Н (рис. 2.12) называется расстояние по отвесному направлению от данной точки (А´; В´´) до принятой основной уровенной поверхности MN. Числовое значение высоты точки называется отметкой. Высоты, отсчитываемые от основной уровенной поверхности MN, называют абсолютными высотами (АА´; ВВ´´), а определяемые относительно произвольно выбранной уровенной поверхности – условными высотами (В´В´´). Разность высот двух точек или расстояние по отвесному направлению между уровенными поверхностями, проходящими через две любые точки Земли называется относительной высотой (В´В´´) или превышением этих точек h.

В Республике Беларусь принята Балтийская система высот 1977 г. Счет высот ведется от уровенной поверхности, совпадающей со средним уровнем воды в Финском заливе, от нуля Кронштадского футштока.

2.6. Ориентирование направлений в топографии
и геодезии

Ориентировать линию местности – значит определить ее направление относительно другого направления принятого за исходное. В топографии и геодезии исходными направлениями для ориентирования приняты географический меридиан, магнитный меридиан и осевой меридиан геодезической зоны, которые на топографических картах соответственно обозначаются: – линией со звездочкой (); – линией со стрелкой (­) и линией с угольником на конце (U) .

Направление географического меридиана получают из астрономических наблюдений, а направление магнитного меридиана определяет свободно подвешенная и уравновешенная магнитная стрелка. Магнитная ось стрелки в каждой точке земной поверхности совпадает с направлением магнитного меридиана этой точки.

Географическим азимутом А направления, называется горизонтальный угол А, измеренный по ходу часовой стрелки от северного направления географического меридиана, проходящего через данную точку до ориентируемой линии (рис. 2.13). По абсолютному значению азимуты изменяются от 0 до 360°. На рисунке горизонтальные углы А₁, А₂, А₃, А₄ будут географическими азимутами ориентируемых направлений О1; О2; О3; О4. Точка О – начало ориентируемых направлений; а линия СЮ – географический меридиан точки О.

Магнитным азимутом направления называется горизонтальный угол А_м между северным направлением магнитного меридиана и направлением данной линии, отсчитываемый по ходу часовой стрелки (рис. 2.14). Вследствие не совпадения географических и магнитных полюсов магнитный и географический меридианы в данной точке земной поверхности образуют между собой угол d, называемый склонением магнитной стрелки (рис. 2.14).

Магнитное склонение может быть восточным – положительным, если северное направление магнитного меридиана находится к востоку от географического и западным – отрицательным, если северное направление магнитного меридиана проходит к западу от географического.  Зависимость между географическим и магнитным азимутами выражается формулой А = А_м + d.

Склонение магнитной стрелки изменяется в зависимости от места и времени. Различают: суточные, годовые и вековые изменения склонения. Кроме того, величина склонения изменяется под влиянием магнитных бурь, связанных с полярным сиянием, солнечной активности, землетрясений, в районах магнитных аномалий и т. д. Суточные колебания склонения магнитной стрелки не превышают 5–15¢. Вследствие этого, ориентирование по магнитному азимуту проводится лишь в тех случаях, когда не требуется большая точность.

В топографии и геодезии применяется также ориентирование направлений относительно северного направления оси абсцисс в системе прямоугольных координат. Угол, отсчитываемый от северного направления оси абсцисс или линии параллельной ему до данного направления, по ходу часовой стрелки называется дирекционным углом a (рис. 2.15). Дирекционный угол изменяется от 0⁰ до 360⁰.

Угол между географическим меридианом данной точки и северным направлением оси абсцисс (вертикальной линией координатной сетки) называется сближением меридианов g (рис. 2.15). Сближение меридианов бывает восточным со знаком плюс и западным со знаком минус. При восточном сближении меридианов, линии параллельные осевому меридиану отклоняются к востоку от географического меридиана, проходящего через эту точку, а при западном – к западу. Зависимость между географическим азимутом и дирекционным углом выражается формулой А = a + g.

Для того чтобы перейти от дирекционного угла к магнитному азимуту необходимо знать две величины – склонение магнитной стрелки и сближение меридианов. Данные об этих величинах в виде графика и текста помещаются под южной рамкой топографической карты. Магнитный азимут равен разности дирекционного угла и поправки направления А_м = a – П. Поправка направления П – это угол между магнитным меридианом и северным направлением оси абсцисс. Поправка вычисляется по формуле .

Иногда ориентирование линии выражается острыми углами – румбами r. Румбом называют острый угол, отсчитываемый от ближайшего направления меридиана (северного или южного) до данной линии (рис. 2.16). Румбы имеют значения от 0° до 90° и сопровождаются названием четверти в которой проходит линия. Румбы переводят в азимуты и дирекционные углы и наоборот (табл. 2.4).

Таблица 2.4

Зависимость между азимутами или дирекционными углами и румбами линий, расположенных в разных четвертях, устанавливают по формулам.

7. Связь между полярной и прямоугольной

системами координат

В геодезии угловые измерения выполняются в полярной системе координат, а нанесение на карту пунктов и объектов местности более точно производится по их прямоугольным координатам. Перевычисление полярных координат к прямоугольным и наоборот производится по формулам прямой и обратной геодезических задач (рис. 2.17).

Прямая геодезическая задача состоит в том, что по известным координатам точки А (Х_А;Y_А), горизонтальному проложению S линии АВ и дирекционному углу , вычисляют приращения координат х ; у и координаты точки В (Х_В;Y_В). Приращениями координат х и у называются разности координат конечной В и начальной А точек линии АВ. Значения приращений определяются из прямоугольного треугольника АВС по заданным S и :   х= S cos ; у = S sin . В зависимости от названия четверти прямоугольной системы координат приращения х и у имеют определенные знаки (см. табл. 2.3).